
|
15-494 Cognitive Robotics Spring 2010 |
|

|
15-494 Cognitive Robotics Spring 2010 |
|
Part I: Using SIFT for Object Recognition
Chang to the directory ~/Class/sift-tool and then typee
./sift-tool. Tell it you are creating a new object
library. Then click on "Create new object", go to the
"sift-tool/images" subdirectory, select "cherrylimeade", and select
the first image file in that directory. Name your object Cherry
Limeade.Click on Cherry Limeade in the SIFT Objects Explorer window, and then click on "Add exemplar". This time select the second image in the cherry limeade directory as your training data. Blue squares in the input image denote new (unfamiliar) keypoint descriptors; yellow squares denote familiar keypoints, i.e., they match an existing model; pink squares denote features of the selected model that the image did not match. Create another object called "Duck" that you train on the first two images from the "duck" directory. Then train on image #5 from the "duck" directory, and notice that the program decides to create a second model for this object because the first model does not match this new image well enough. Train the program on images from the "doubleshot" directory as well. Click on the "Find all known objects in image" button and select a new image from one of the three object categories you trained on. Look in the "Matched Model Information" window to see the match results. How well does the program do at recognizing novel views of trained objects? Click on one of the yellow or magenta feature boxes in the Input Image window, and you can see information about that feature. Recall that sift features or "keypoint descriptors" are histograms of local gradients selected as a scale space extramum point. Part II: Simple Gestalt Perception
Take 5-6 blue game pieces and lay them out in a circle. Place 1-2
pink game pieces inside the circle, and some outside it. Your task is
to decide which pink pieces are in the circle. Use the camera space
for this task.
To solve this task, start by extracting ellipses, as you've done before. (Use the MapBuilder for this.) Then form the convex hull of the blue ellipses, using PolygonData::convexHull. Render the resulting Shape<PolygonData> to produce a sketch of the region enclosed by the blue pieces. Check each pink ellipse to see if it falls within the region. Mark the ones that do, and produce a result sketch indicating which ellipses are marked. Note: you may prefer to take some pictures and then work in the simulator rather than on the robot. That's fine. Also, you can choose any two colors of easter eggs for this problem; you don't have to use blue and pink. Part III: Non-Convex Boundaries
In the children's game of "tag", a certain region is designated as
"home base", and any player standing within it is safe and cannot be
tagged. In the image below, where players are represented by green
ellipses and the boundary of home base by pieces of pink tape, only
one of the two depicted players is safe.
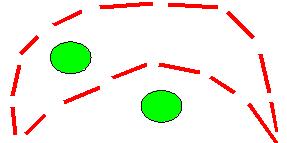 Question 1: What result would convex hull produce if you use it to determine whether a player is safe? Question 2: What principle(s) of gestalt perception does the convex hull algorithm violate when used on a non-convex apparent boundary? Explain your reasoning. To correctly determine inside/outside relationships in this case you must construct the boundary of "home base" some other way, without using convex hull. There are various ways you could do this. The best way is to use the line extractor to find pink line segments, and then consider each of the two line endpoints. However, the line extractor may not work well on short, distant lines, so you could use blobs to represent all the little pieces of tape that aren't perceived as lines, and take the centroid of each blob using getCentroid(). Use the minBlobAreas field of your MapBuilderRequest to eliminate any noise. Given this set of line endpoints and blob centroids, put the points in appropriate order to traverse the circumference of the convcave region. (Hint: start with one point, select the point closest to it, select the point closest to that one, etc., until all points have been selected. But once you've selected one endpoint of a line, your next choice must be the other endpoint.) You can then feed a vector of points (vertices) to the PolygonData constructor to make a polygon. Use visops::fillInterior() on the rendered polygon to solve the inside/outside problem. Finish this problem for homework if you don't complete it during the regular lab period. Hand in your code, your answers to Questions 1 and 2, and a snapshot of the sketch showing your polygon and results by Friday, March 19. Extra credit: solve the non-convex boundary problem in local space instead of camera space. You will need to use MapBuilderRequest::localMap and set pursueShapes to true. Note: rendering shapes in local or world space requires special tricks we haven't discussed. So instead of using sketches in your solution, solve the problem using PolygonData's isInside() predicate, and present your answer by changing the colors of the inside ellipses from yellow to blue, via setColor(). Dave Touretzky and Ethan Tira-Thompson |