1. Introduction
Multicast has been a proposed IETF standard for over a decade [7], and the experimental MBone network has been operational since 1992 [5,13]. There is strong industry push to deploy IP multicast in the Internet proper, yet the single biggest economic concern remains: how should multicast be priced [25]?
It is important to recognize at the outset that multicast as a network service will be used by many different applications. These could range from multimedia teleconferencing and distributed interactive simulation to software distribution, webcasting and other "push" applications. These applications have very different bandwidth/latency requirements and scaling characteristics. They compete for network resources not just against one another, but against unicast traffic as well. Therefore, any resource allocation scheme will have to be non-discriminatory between applications and traffic types (unicast vs. multicast).
This paper advocates a cost-based approach to multicast pricing. When prices are set to reflect actual network resource consumption, they minimize market distortion and result in efficient and equitable resource allocation. Additionally, this paper calls for pricing multicast relative to the corresponding unicast service. If unicast is subject to a flat-rate pricing scheme, multicast should also be subject to a flat-rate pricing scheme; if unicast traffic becomes subject to a usage-based pricing regime, then multicast should be priced according to usage as well. As long as multicast is priced relative to unicast, all the results in this work are valid under either pricing regime. More importantly, economic theory reminds us that prices serve as market signals to the users, providing feedback regarding their usage of network resources. Given a tariff structure where multicast and unicast services are priced consistently with each other, the end user will correctly choose multicast over unicast when it is indeed the cheaper (and more efficient) alternative.
The structure of this paper is as follows. We begin in Section 2 with the quantification of multicast link usage. This allows us to capture the economies of scale realizable by multicast. The cost structure thus established is then applied to the pricing design in Section 3. Finally, Section 4 looks at how dense and sparse mode multicast should be priced to reflect the difference in bandwidth usage between the two modes.
2. Cost Quantification
Multicast achieves bandwidth savings over unicast by duplicating packets (to multiple destinations) only when routing paths diverge. By avoiding the transmission of duplicate packets over any link, significant economies of scale over unicast can be realized.
This work focuses on the quantification of bandwidth usage, i.e. link cost, as opposed to node costs, such as routing table memory, CPU usage, etc. After all, multicast can be thought of as the result of an engineering-economic optimization, where significant bandwidth savings is realized at the expense of control and processing overhead at the routing nodes. This tradeoff is justified because the cost of transmission has, historically, declined at a slower rate than the cost of processing/memory (Figure 1). It is debatable whether this cost gap between transmission and processing will persist, given the breakthroughs in optical amplification and wave-division multiplex (WDM) technologies, and the diminishing returns from further transistor size shrinkage. Node costs may also become significant for multicast for another reason: multicast employs logical addresses in a flat addressing space, and hence CIDR-style route aggregation [21] is not possible. Address depletion will not be the direct limit to scalability, especially if the Internet moves to IPv6 [9]. Instead, routing table entries will become the scarce resource since every single multicast group will require its own separate entry. For source-based multicast trees, this cost will have to be multiplied M times for each multicast group with M active senders. At some point in the future it may become necessary to institute some market-driven or administrative mechanism for multicast address allocation [14,22,23].
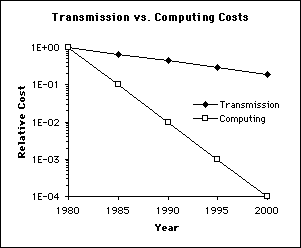
Figure 1. Transmission vs. computing cost trends. Source: Spragins et al., Telecommunications: protocol and design, p 25. 1991.
There are several studies that compare the performance and resource costs of various multicast routing protocols [3,12,24,29,30]. In addition to link usage (as measured by tree costs), the different protocols are also evaluated in terms of delay and traffic concentration metrics. All of these studies, however, only compare multicast protocols against one another, rather than against a unicast baseline. This precludes any direct computation of how much bandwidth savings is realizable if one switches from unicast to multicast.
A recent measurement study on MBone traffic provides some empirical data on the nature and characteristics of multicast traffic [1]. The study finds that "while there is a direct relationship between the number of unicast packet-hops and the number of receivers, the number of multicast packet-hops remains nearly flat. Even when the number of group members increases, the number of packet hops increases only slightly". This result is limited, however, by the narrow range of membership size (50-200 receivers out of ~5000 MBone nodes, or 1-4% subscription rate) sampled in the study. As this paper shall demonstrate, multicast cost does indeed rise with membership size, albeit at a slower rate than unicast.
2.1. Quantifying Multicast Tree Cost
A network provider offering multicast service would be interested in quantifying the link usage of a multicast delivery tree. Specifically, for a multicast group of membership size N, we can express the (normalized) multicast tree cost as:
Lm/Lu = Nk (1)
Lm: total length of multicast distribution tree;
Lu: average length of unicast routing path;
N: multicast group size;
k: economies of scale (EoS) factor, ranging between 0 and 1.
The total length of a multicast tree, Lm, is simply the summation of edge costs of all links that make up the tree. These edge costs may have weight metrics that are hop-based and/or distance-based. In this study we choose the hop-based approach, i.e. setting the cost of all edges at unity. This is consistent with general Internet routing today, where hop-count is the widely-used metric for route cost calculations [i].
Without any loss of generality, we normalize Lm by Lu. This means that the normalized multicast tree cost, Lm/Lu, is a dimensionless parameter. Lu is the expected path length between any two nodes in the network. Equivalently it is the average distance a unicast packet will have to travel from the source to the destination in this network. Lu is clearly network-specific -- it is influenced by topological factors such as the number of nodes and links in the network, average node degree, network diameter, etc. Its value, however, should be relatively static and well understood by the network provider.
N is the number of receivers in the multicast group. It is important to realize that we are referring to the network routing nodes rather than the individual hosts in this context. There may be one or more hosts, and therefore one or more potential multicast group members, attached to each leaf router. However, for a variety of reasons [ii], the leaf router may not have an accurate count of the total number of hosts belonging to a group. Indeed, such an accurate count is not required. The leaf router will join (or remain on) the multicast tree as long as one or more local hosts is in the multicast group. It does not know (or care) who or how many hosts are in the group. The number of routing nodes that have subscribed hosts -- rather than the actual number of subscribed hosts -- is the more meaningful definition of multicast group size, because it is the former which determines resource consumption in the provider's network. This definition of membership size has some interesting ramifications, as we shall see in Section 2.4.
We use the factor k to capture the extent of economies of scale realizable via multicast. In addition to quantifying this EoS factor, it is also important to study and characterize its dependence on (or independence of) different network variables, such as network size, topology, membership size, distribution, etc.
It is trivial to come up with extreme spatial distributions of receivers that will result in scenarios of k = 0, k = 1, or anything in between. Consider the simple network in Figure 2, where a sender is sending data to two separate multicast addresses. For the first multicast group, the receivers are downstream from the source router via different links, and so no link savings are realizable (k ~= 1). On the other hand, the receivers in the second multicast group lie in a common distribution path, and significant link savings are realizable (k ~= 0). For generality, this study assumes that receivers are randomly distributed throughout the network.
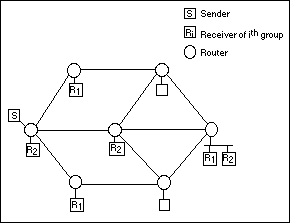
Figure 2. Example network shows that degree of link savings achievable is strongly dependent on spatial distribution of receivers.
2.2 Methodology
Figure 3 provides a pictorial overview of the methodology used in this study. Shortest-path multicast trees are constructed, using Dijkstra's algorithm [10], over a variety of networks and receiver sets. This allows us to quantify the cost of multicast trees, validate the relationship of equation (1), and determine the EoS factor k.
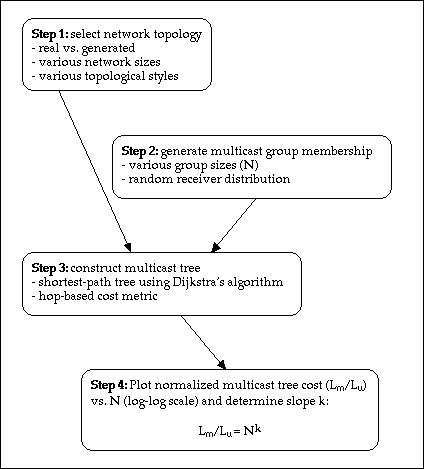
Figure 3. Quantifying economies of scale in multicast communication - a process overview.
To determine if the size and topological style of the networks affect
multicast tree costs, we employ real and generated networks that are
representative of inter-domain routing topologies of the Internet. These
networks consist of routing nodes and interconnecting links. Real network
topologies are gathered from the MBone [iii]
and the early ARPANET. Network generation tools (GT-ITM and tiers
[4,11,31]) are utilized to produce realistic networks
of different topological styles, as illustrated in Table 1.
Through user-specified parameters, we can control the style and size of the networks generated by the network generation tools. Specifically, by controlling parameters on edge probabilities, we are able to generate networks with average node degrees consistently in the range of 3 to 4, which is typical of present-day networks. (For a network with N nodes and M links, its average node degree is 2*M/N.) Please refer to [4,11,31] for more details on the use of these tools.
Ten different topologies are created for each of the five generated network styles; ten sets of receiver distributions are generated for each group membership size. For the arpa and mbone networks, where single real topologies are available, a hundred sets of receiver distributions are generated. Therefore, all data points in the following plots have a sample size of 100.
| Name |
Type |
Source/Tool used |
Topological Style |
# of Nodes |
# of Links |
Avg. Node Degree |
| arpa |
real |
ARPANET |
- |
47 |
68 |
2.89 |
| mbone |
real |
MBone |
- |
5019 |
9310 |
3.71 |
| r100 |
generated |
GT-ITM |
random |
100 |
169.4 |
3.39 |
| ts100 |
generated |
GT-ITM |
transit-stub |
100 |
181.1 |
3.62 |
| ts1000 |
generated |
GT-ITM |
transit-stub |
1000 |
1819.0 |
3.64 |
| ti1000 |
generated |
tiers |
hierarchical |
1000 |
1681.5 |
3.36 |
| ti5000 |
generated |
tiers |
hierarchical |
5000 |
8837.0 |
3.35 |
2.3 Results
The results of our analysis confirm that the cost of multicast trees can indeed be approximated by Equation (1), and that the economies of scale (EoS) factor k falls within a narrow range for reasonable network conditions. This implies that the Lm/Lu ratio is an exponential function of the number of receivers in the multicast group, N. Figure 4 shows that this exponential relationship applies for all three topological styles (random, transit-stub, hierarchical) of generated networks, and the value of k lies in the 0.8 range (standard deviations are shown with error bars).
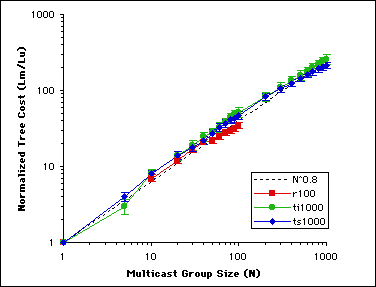
Figure 4. Normalized multicast tree length as a function of membership size - slope is constant (~0.8) across various network topological styles.
Figure 5 shows the same Lm/Lu ratio for two networks,
one with 1,000 nodes and the other with 5,000 nodes. From this plot it is
apparent that the slope k (again ~0.8) is independent of the total number of
network nodes. For example, a 500-member multicast group in a 1,000-node
network (50% subscription rate) will realize a similar EoS factor as a
500-member group in a 5,000-node network (10% subscription rate). This
important result shows that it is the absolute number of nodes that are
receivers in a group, not the percentage of nodes that are receivers , that
should be used as an indicator for multicast tree cost.
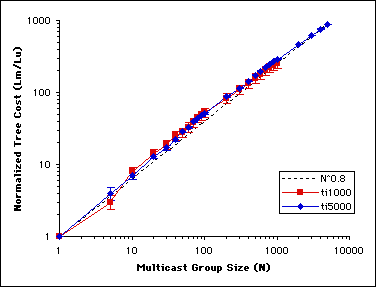
Figure 5. Normalized multicast tree length as a function of membership size - slope is constant (~0.8) across various network sizes.
Figure 6 confirms that the relationship holds for real network topologies
of vastly different sizes, namely the early ARPANET and the MBone topology of
1996. The EoS factor k is again closely bounded in the 0.8 range.
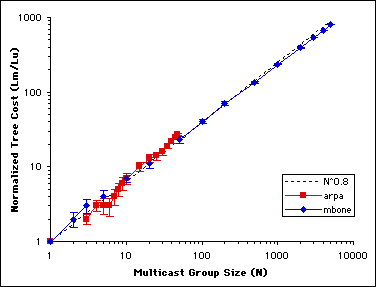
Figure 6. Normalized multicast tree length as a function of membership size - results confirmed with real networks.
2.4 Tree Saturation
As we have indicated in Section 2.1, multiple hosts on a same subnet attached to a leaf router may all be part of a multicast group, but they only count as one receiver from the router's point of view. From a cost-accounting perspective, this result is actually desirable, since the incremental cost of serving additional receivers on a shared broadcast capable subnet is zero. Even where the subnet is non-broadcast, as with ISP POPs, the subnet costs are typically covered by direct subscriber network access charges. However, the presence of multiple hosts per leaf router also leads to the tree saturation effect, which manifests itself in topologies with large local fanouts.
Tree saturation is best illustrated by the example of a realistic national ISP, which has 1,000 dial-in ports at each of its 100 points-of-presence (POPs). This means that the ISP can have up to 100,000 individual hosts connected to the network at any given time. Probabilistically, it takes just ~500 randomly distributed hosts (0.5% of total host population) to join a multicast group before all the POPs have at least one group member [iv]. At this point, the multicast delivery tree is "fully grown" or "saturated", and additional group members can be served at essentially zero incremental cost. Figure 7 gives an illustration of this tree saturation effect. Note that the x-axis is now the number of subscribing hosts, rather than the number of POPs with subscribers.
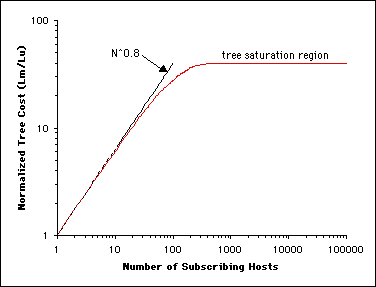
Figure 7. An illustration of the "tree saturation" effect: it takes just ~500 randomly selected dial-in ports (or 0.5% of all ports) to subscribe to a multicast group before all 100 network nodes become part of the multicast tree. All subsequent subscribers can be served at no additional cost.
3. Multicast Pricing
Since multicast tree cost can be accurately predicted from its membership size, we can directly apply the cost expression of Equation (1) into a simple price relationship:
Pm/Pu = Nk' (2)
Pm: price of multicast stream to N nodes, relative to
Pu: price of unicast stream to a single receiver;
k': network-specific EoS factor (empirically derived).
This relationship holds regardless of whether unicast traffic is subject to per-packet (usage-sensitive) or per-month (flat-rate) pricing. Clearly, this gives us a very strong motivation to price multicast as a function of N, the multicast group size.
The price relationship of Equation (2) is applicable even if we are operating in the "tree saturation" regime. In this case, N should simply be set to NTOT, the total number of nodes in the network. For example, an ISP with 100 POPs and k' = 0.8 would set the price ceiling of its multicast service to be 100^0.8 or 40 times that of its unicast service.
It is important to realize that this pricing approach is different from a flat-rate pricing approach [v]. In the latter case, all multicast streams are priced at a flat rate, even if there is only a small number of receivers, and the tree is far from reaching saturation. Of course, a flat-rate pricing approach avoids the accounting overhead associated with traffic metering. However, this pricing scheme would favor applications with large numbers of receivers, at the expense of other applications with fewer receivers. Consequently, applications with fewer than Pm/Pu receivers (e.g. teleconferencing between several parties) will not opt for multicast even though it is more bandwidth efficient.
The current pricing scheme can be characterized as a two-part pricing scheme. Multicast traffic is charged according to N (raised to the 0.8 power) until N reaches NTOT, at which point the price ceiling takes effect. This two-tiered approach would ensure that the multicast service is made available to all traffic types in a non-discriminatory manner.
3.1 Membership Accounting
One practical question remains: how can N be determined for multicast traffic, and at what accounting cost? We first recognize that the receiver-initiated nature of IP multicast precludes centralized knowledge of membership size. Examination of multicast packets is fruitless because the destination address in the packet header is a logical one, revealing nothing about the number and locations of the receivers. Secondly, multicast group membership can change in real time. Receivers may join or leave the group at any point in time, and the multicast tree will be dynamically grafted or pruned accordingly. Any snapshot at the beginning or end of a multicast session will not necessarily yield an accurate picture of the group membership.
As pointed out by Shenker et al., multicast pricing is an inherently non-local problem [25]. Therefore membership accounting has to be achieved via distributed metering. One approach might be to count the number of multicast routers that are part of the multicast tree. In the case of reservation-based traffic, membership accounting might be achieved by the monitoring of QoS reservation signaling (e.g. RSVP). Network measurement and accounting software are commercially available [vi] for installation as edge-metering devices to capture the necessary information for accounting and billing purposes.
It is worth reiterating that the membership size thus captured will only indicate the number of network nodes with subscribing hosts, NR, not the total number of subscribing hosts, NH. From the network's point of view, it is concerned with the bandwidth usage of the multicast tree, whose cost is dependent on NR. Therefore, it is economically efficient for the network provider to price its multicast service as a function of NR. The end user, on the other hand, has to take NH into account when comparing the multicast and unicast alternatives. In the case of unicast, the sender has to transmit a duplicate copy of data to each of the NH destination hosts [vii]. For multicast, the membership size will be NR, with NR < NH, since some of the hosts may be attached to common routing nodes. The sender would choose multicast over unicast as long as Pm, which is equal to (NR^0.8)*Pu, is less than NH*Pu.
3.2 Other Issues
This paper does not address the issue of cost allocation and settlement [16], except by noting that receiver-initiation does not necessarily imply that the charges have to be split among the receivers. There are many instances in telephony, for example, where the payment party is different from the initiating party. Assigning all multicast charges to the sender would result in a simpler billing system because (i) it is consistent with the unicast paradigm, i.e. meter and charge at the network entry point, and (ii) it avoids the ambiguities involved in equitably splitting the charges among multiple receivers. Out-of-band settlements are always available if needed.
This paper addresses multicast pricing at the network layer (layer 3). When we look at reliable multicast at the transport layer (layer 4), we recognize that multicast retransmission traffic patterns may not be as predictable as unicast. There are various multicast transport protocols being proposed and developed [19]. Depending on the number of receivers and the protocol used, the number of retransmitted packets may be comparable, if not more than the number of original data packets, even at a low packet-loss rate. Since reliable multicast is still in the development and definition phase, it is important to ensure that multicast pricing schemes at the network layer properly influence the choice of reliable multicast protocol at the transport layer.
4. Dense vs. Sparse Mode Multicast
Many different flavors and generations of multicast routing protocols have been proposed [2,8,18,26,28], of which several have been implemented on the MBone. They can be classified into either dense mode (DVMRP, PIM-DM) or sparse mode (CBT, PIM-SM). In addition to bandwidth usage, there are many other dimensions to the tradeoff between DM and SM multicast, and these have been extensively studied elsewhere [3,12,24,29,30]. As a general rule of thumb, DM multicast is perceived to be appropriate for mass-dissemination applications such as webcasting, whereas SM multicast is more suited for teleconferencing and other applications with just a few receivers. The question is: should dense and sparse mode multicast be priced differently?
Dense and sparse mode protocols differ primarily in their tree-construction techniques. Dense mode protocols take a flood-and-prune approach, where data packets are periodically flooded to the entire network, and branches are pruned where there are no downstream receivers. Sparse mode protocols, on the other hand, grow the distribution tree on a branch-by-branch basis as new nodes join the multicast group. Dense mode protocols work well when most nodes in the network are receivers, but are extremely bandwidth inefficient when the group members are few and sparsely located throughout the network.
We can incorporate the control overhead into the cost model we have developed, thus allowing a comparison of the total bandwidth usage between SM and DM multicast (and unicast and broadcast as well). Table 2 shows the link cost (measured in packet-hops per second) for transmitting data to a set of N receivers at a data rate of Q packets/second. Lm and Lu are the multicast tree lengths and unicast path lengths as before:
| Type |
Data |
Control Overhead |
| unicast |
Q * N * Lu |
- |
| multicast (sparse mode) |
Q * Lm |
Lm/tsm |
| multicast (dense mode) |
Q * Lm |
2(Lm'-Lm)/tdm |
| broadcast |
Q * Lm |
Q * (Lm'-Lm) |
For unicast, no control overhead is necessary to coordinate the multiple receivers; the sender simply transmits one packet to each of the N receivers, and each receiver is on average Lu hops away from the sender. For sparse mode multicast, a tree of length Lm is constructed for packet delivery. The maintenance of this tree requires a periodic transmission of control messages. Once every tsm seconds, receivers have to reannounce their intention to remain on the tree by sending out a refresh message. Otherwise the link from which incoming packets are received will be pruned from the multicast tree. Regardless of how many receivers are downstream of a link, only one refresh message is required for each of the Lm links per refresh period. Dense mode multicast, on the other hand, takes a flood-and-prune approach. Periodically (once every tdm seconds) all multicast forwarding states time out and the data packet is broadcast to all nodes in the network. Then those nodes who have no downstream receivers will send a `prune' message to remove itself from the tree. If Lm' is the length of the broadcast tree, then there will be (Lm' - Lm) links on which an unwanted data packet will trigger the transmission of a `prune' message in the reverse direction. Finally, for broadcast communication, each of the Lm' links will carry a copy of the data packet. However, for (Lm' - Lm) of these links, the data packet will be discarded, and hence these are classified as overhead in Table 2.
The impact and significance of the control overhead is dependent on the data rate a and the timeout periods. For the current multicast protocols, both tsm and tdm are on the order of minutes. Figure 8 shows the total link cost (data and control) needed to transmit a single data packet to N receivers in the MBone network using the various alternatives. As expected, the link cost for unicast is linearly proportional to the number of receivers, and the link cost for broadcast is constant. We also observe a crossover from sparse to dense mode multicast as the number of receivers increases. However, we make the interesting observation that dense mode multicast is never the least-cost option in this scenario except when all nodes are receivers. In fact, for the transmission of a single data packet, broadcast is the preferred approach when more than 40% of nodes are receivers. This suggests the cost of control messages may be prohibitively high for very low data-rate applications.
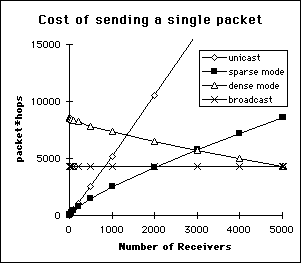
Figure 8. Comparing alternatives for sending one data packet to receivers in the MBone network.
Figure 9 shows the same cost comparison when we move to a data rate of 5kbps (which is a conservative lower bound for most file transfer and multimedia applications). Unicast and broadcast are both unattractive except at the boundaries. Dense and sparse mode multicast appear to do equally well at all subscription density levels.
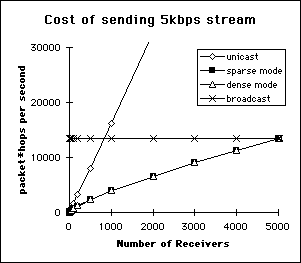
Figure 9. Comparing alternatives for sending a 5kbps data stream to receivers in the MBone network - there appears to be no difference between sparse and dense mode multicast.
Upon normalization to unicast cost, and replotting in log-log scale, Figure 10 reveals that there is a significant overhead associated with DM multicast at low subscription density levels. In fact, DM multicast is worse than unicast if there are less than ten receivers in the group (or 0.2% subscription density). On the other hand, when all network nodes are receivers (an unambiguously "dense" situation), DM does not perform significantly better than SM [viii]. We observe that the SM cost curve maintains a slope of ~0.8. This echoes our earlier results, and corroborates previous findings that overhead traffic amounts to no more than 1% of total traffic for SM multicast [3].
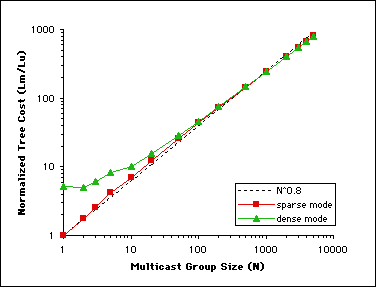
Figure 10. Comparing dense and sparse mode multicast for sending a 5kbps data stream to receivers in the MBone network - dense mode multicast clearly consumes more bandwidth when there are few receivers, but the two modes are comparable with subscription density as low as 4% (about 200 receivers).
These results confirm that teleconferencing type applications can only be efficiently supported by sparse mode multicast. Dense mode multicast, on the other hand, will likely serve the webcasting market, where the groups are typically larger and less dynamic. Therefore, dense and sparse mode multicast services should be priced such that users select the appropriate mode based on their expectation of the group membership size.
One possible pricing approach is to offer DM multicast at a flat-rate while pricing SM multicast according to membership size. This way, applications with large numbers of receivers would opt for DM and its flat charge, while those with few receivers would choose the membership-sensitive tariff of SM. This approach might be justified by the fact that tree saturation is more likely to occur for webcasting scenarios. Furthermore, if we expect metering costs to be proportional to the number of receivers, then it may make economic sense to meter SM but not DM group memberships.
On the other hand, it is also entirely possible that SM multicast will become the general-purpose multicast vehicle, displacing DM multicast altogether. As illustrated by Figure 10, DM has little if any competitive advantage over SM multicast on a strictly link-usage basis. If this scenario occurs, SM multicast should be priced according to a two-tier approach as described in Section 3. This is the only way to ensure that multicast is available to both teleconferencing and webcasting application-types in a non-discriminatory fashion.
5. Conclusion
Through the quantification of multicast link usage, this work has demonstrated that the cost of a multicast tree varies at the 0.8 power of the multicast group size. This result is validated with both real and generated networks, and is robust across topological styles and network sizes. Practically, this means that the cost of a multicast tree can be accurately predicted given its membership size.
If a network provider takes a cost-based approach to multicast pricing, as advocated by this paper, the above result provides a strong motivation to price multicast according to group size. Recognizing the effect of tree-saturation, a price ceiling should be incorporated into the price schedule, with the ceiling set precisely at the tree saturation level. This two-part tariff structure is superior to either a purely membership-based or a flat-rate pricing scheme, since it reflects the actual link usage at all group membership levels. Undesired subsidies between mass-dissemination applications (e.g. webcasting) and those with few receivers (e.g. teleconferencing) are eliminated, allowing the multicast service to be available to all applications in a non-discriminatory manner.
Explicit accounting of the control overhead allows a comparison of dense and sparse mode multicast within our cost framework. We find that sparse mode multicast maintains the exponential relationship between group size and cost, while dense mode multicast is inefficient at extremely low membership levels. This suggests that, in the event when both multicast modes co-exist to serve different markets, dense mode multicast is a good candidate for flat-rate pricing and the mass-dissemination market, while sparse mode multicast is a good candidate for pricing based on membership size and the teleconferencing market.
Notes
[i] As pointed out by [20], results based on hop-based metrics are generalizable to both source-based shortest-path trees and minimal spanning trees. Our results will not be significantly different even if we adopt a hop-distance hybrid metric (using a rule of thumb [17] that 100 kilometers of link distance have equivalent cost to one hop), as the majority of links are short-haul links.
[ii] According to version 2 of the IGMP protocol [15], "multicast group membership means the presence of at least one member of a multicast group on a given attached network, not a list of all of the members". When a host wishes to join a group, it should transmit a 'REPORT' message (and up to two additional 'REPORT' messages for redundancy) in case it is the first member of that group on the network. However, a host is not required to send a 'LEAVE' message when it leaves the group. Furthermore, to avoid report implosion, multiple responses to periodic 'General Query' messages are suppressed. Therefore, the router cannot infer, from the accounting of 'REPORT' and 'LEAVE' messages, the local multicast group size.
[iii] MBone network topology from 7/30/1996; available from http://www.nlanr.net/Caidants/Mrwatch.data.tar.gz
[iv] The expected number of subscribing hosts (sampling with replacement, for simplicity) needed to place all M points-of-presence on the tree is:
For M = 100, E[N] = 519. For the actual case where we have sampling without replacement, the expected number would be even lower.
[v] UUNET, the pioneer in IP multicast deployment, currently adopts a flat-rate pricing approach with a Pm/Pu ratio of ~400 [27]. But its president is also predicting an Internet-wide switch to usage-sensitive pricing in the near future.
[vi] One example is Cisco's NetFlow software [6], which can be configured to support various charging schemes such as QoS-based charging and distance-sensitive charging.
[vii] We do not consider the case where proxy caches are installed at the edges of the network, in which case subsequent requests from the same subnet may be satisfied from the local copy. This would mean that the sender would only need to transmit NR copies even in unicast mode.
[viii] The precise crossover point between SM and DM is highly variable from one topology to the next, but the two curves always approach the k=0.8 slope asymptotically. This suggests that there can be no meaningful formula or numerical expression for the "sparseness" or "denseness" of a multicast group.
Acknowledgment
This work is supported by the National Science Foundation under Cooperative Agreement No. IRI-9411299 and by the Council on Library and Information Resources A. R. Zipf Fellowship. The authors wish to thank Hui Zhang for comments on an earlier version of this paper. All views and conclusions in this paper are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the National Science Foundation, the U.S. Government, or the Council on Library and Information Resources.
References
[1] Almeroth, K. and M.H. Ammar. Multicast group behavior in the Internet's multicast backbone (MBone). IEEE Communications Magazine, June 1997.
[2] Ballardie, T., P. Francis and J. Crowcroft. Core based trees (CBT) an architecture for scalable multicast routing. In Proceedings of ACM SIGCOMM 1993.
[3] Billhartz, T., J. B. Cain, E. Farrey-Goudreau, D. Fieg and S. Batsell. Performance and resource cost comparisons for the CBT and PIM multicast routing protocols. IEEE Journal on Selected Areas in Communications 15(3), 1997.
[4] Calvert, K., M. Doar and E. W. Zegura. Modeling Internet topology. IEEE Communications Magazine, June 1997.
[5] Casner, S. and S. Deering. First IETF internet audiocast. ACM Computer Communication Review, July 1992, p92-97.
[6] Cisco. NetFlow. White paper, August 1997. <URL:http://www.cisco.com/warp/public/732/netflow/nflow_wp.htm>
[7] Deering, S. Host extensions for IP multicasting. RFC 1112, August 1989. Supersedes RFC 1054, May 1988 and RFC 988, July 1986.
[8] Deering S., D. Estrin, D. Farinacci, V. Jacobson, C.-G. Liu and L. Wei. The PIM architecture for wide-area multicast routing. IEEE/ACM Transactions on Networking, 4(2): 153-162, 1996.
[9] Deering S. and R. Hinden. Internet protocol, version 6 (IPv6) specification. RFC 1883, 1995.
[10] Dijkstra, E.N. A note on two problems in connection with graphs. Numerical Math 1: 269-71, 1959.
[11] Doar, M. A Better Model for Generating Test Networks. In Proceedings of Globecom 1996.
[12] Doar, M. and I. Leslie. How bad is naive multicast routing? In Proceedings of IEEE INFOCOM 1993, San Francisco CA, p82-89.
[13] Eriksson, H. MBone: the multicast backbone. Communications of the ACM 37(8):54-60, 1994.
[14] Estrin, D., M. Handley, S. Kumar and D. Thaler. The multicast address set claim (MASC) protocol. Work in progress, November 1997. <URL:http://ietf.org/internet-drafts/draft-ietf-idmr-masc-00.txt>
[15] Fenner, W. Internet group management protocol (IGMP), version 2. RFC 2236, 1997.
[16] Herzog, S., S. Shenker and D. Estrin. Sharing the "cost" of multicast trees: an axiomatic analysis. In Proceedings of SIGCOMM 1995.
[17] Mahdavi, J. Personal communications, November 1997.
[18] Moy, J. Multicast extensions for OSPF. RFC 1584, 1994.
[19] Obraczka, K. Multicast transport protocols: a survey and taxonomy. IEEE Communications Magazine 36(1): 94-102, Jan 1998.
[20] Pejhan, S., M. Schwartz and D. Anastassiou. Error control using retransmission schemes in multicast transport protocols for real-time media. IEEE/ACM Transactions on Networking, 4(3): 413-427, 1996.
[21] Rekhter, Y. and T. Li. An architecture for IP address allocation with CIDR. RFC 1518, 1993.
[22] Rekhter, Y. and T. Li. Implications of various address allocation policies for Internet routing. RFC 2008, 1996.
[23] Rekhter, Y., P. Resnick and S. Bellovin. Financial incentives for route aggregation and efficient utilization in the Internet. In Proceedings of Telecommunications Policy Research Conference. Solomons MD. Revised version in "Coordination of the Internet", B. Kahin and J. Keller, eds., MIT Press, 1996.
[24] Salama, H.F., Reeves, D.S. and Y. Viniotis. Evaluation of multicast routing algorithms for real-time communication on high-speed networks. IEEE Journal on Selected Areas in Communications 15(3): 332-45, 1997.
[25] Shenker, S., D. Clark, D. Estrin and S. Herzog. Pricing in computer networks: reshaping the research agenda. Telecommunications Policy 20(3), April 1996.
[26] Thaler, D., D. Estrin and D. Meyer, eds. Border Gateway Multicast Protocol (BGMP): protocol specification. Work in progress, 1997. <URL:http://ietf.org/internet-drafts/draft-ietf-idmr-gum-01.txt>
[27] UUNET Technologies. UUNET announces multicast service for mass Internet broadcasting. Press release, September 23, 1997.
[28] Waitzman, D., C. Partridge and S. Deering. Distance vector multicast routing protocol (DVMRP). RFC 1075, 1988.
[29] Wei, L. and D. Estrin. The trade-offs of multicast trees and algorithms. In Proceedings of ICCCN 1994.
[30] Wei, L. and D. Estrin. Multicast routing in dense and sparse modes: simulation study of tradeoffs and dynamics. University of Southern California Computer Science Technical Report 95-613, 1995.
[31] Zegura, E.W., K. Calvert and S. Bhattacharjee. How to model an internetwork. In Proceedings of IEEE Infocom 1996, San Francisco CA.