Lab #1 Summary

David R. O'Hallaron
 March 3, 1996

The purpose of Lab 1 was to help you understand the relationship between high--level C code and the machine code that actually runs. Most students worked very hard, and although a few did exceptional work, in general I was disappointed with the overall quality of the labs. Here are some general comments to keep in mind for future labs. There is also a summary of the grades at the end.

General comments

Many students stuck together printouts instead of preparing a document. We didn't deduct points this time, but for Labs 2 and 3 you should prepare a document with the following structure: Another common mistake was not running enough iterations to get meaningful numbers from the course-grained Unix timers. This was surprising, since we covered this both in lecture and in the first recitation assignment. I worried that we were belaboring a rather obvious point, but apparently many students still didn't catch on. It's a basic thing, but let me summarize again: you must accumulate hundreds or thousands of timer periods before you can draw meaningful conclusions from the measurements.

This was a difficult lab, but few students came to me (or the other teaching staff) for help. This was probably because many students started too late. The lesson is: start your labs early, and don't be afraid to ask for help. If the office hours don't fit your schedule, demand an appointment!

Problem 1

On the R2000/R3000 systems, double precision add has a 2 clock latency and the multiply has a 5 clock latency. The best approach for determining the latencies is to insert increasing number of nop's between add.d/ or mul.d/ pairs, where uses the result produced by add.d or mul.d. The point where the running begins to increase linearly indicates the latency. For example, the numbers for the looked something like: 
	#nops	time
	0       10   (Mips anomaly discussed in the newsgroup)
	1	9
	2	10   (here is where linearity starts)
	3	11
	4	12

Problem 2

This should have been fairly straightforward. The biggest problem was that measurements were gathered without accumulating enough timer periods. Some students confidently reported numbers that didn't make any sense, such as "each nonzero requires 0.01 clock cycles".

Problem 3

Most students did well on this problem. The basic idea was to perform the crossover analysis using some kind of binary search. The crossover point between sparse and dense representations was typically around 70%.

Problems 4 and 5

Problems 4 and 5 were the core of the assignment. Students had a great deal of trouble with these problems and many didn't make the connections we hoped you would make. There are some basic principles that govern these kinds of optimization problems:
  • The first key idea is to optimize the common case. Focus first on the inner loop, then focus on the outer loop.
  • Another key idea is to eliminate memory references to operands that could just as easily be stored in registers. Changing a memory reference to a register reference is called promoting a variable to a register. Even very good optimizing compilers have trouble promoting variables to registers if they are an array element or if they referenced by a pointer. However, scalars are easily promoted to registers.
  • Pointer code can help to eliminate the incrementing of index variables, and shifts that convert word offsets to byte offsets. In general, though, gains will be small.
Figure 1 shows how I applied these ideas when I did the Lab.
(a) Original C code (b) Promoting z[r] to a register (c) Eliminating an index update 
int r, ci;
for (r = 0; r < M->nrow; r++) {
  z[r] = 0.0;
  for (ci = M->rstart[r];
       ci < M->rstart[r+1]; 
       ci++) {
    z[r] += M->val[ci] * 
            x[M->cindex[ci]];
  }
}

for (r = 0; r < M->nrow; r++) {
  ftype_t temp = 0.0;
  for (ci = M->rstart[r]; 
       ci < M->rstart[r+1]; 
       ci++) {
    temp += M->val[ci] * 
            x[M->cindex[ci]];
  }
  z[r] = temp;
}

int r;
ftype_t *val = M->val;
int *cindex_start = M->cindex;
int *cindex = M->cindex;
int *rnstart = M->rstart+1;

for (r = 0; r < M->nrow; r++) {
  ftype_t temp = 0.0;
  int *cindex_end = 
    cindex_start + *(rnstart++);
  while (cindex < cindex_end) {
    temp += *(val++) * 
            x[*cindex++];
  }
  z[r] = temp;
}

 0x4c: lw      v1,16(t0)
 0x50: sll     v0,a3,2
 0x54: addu    v0,v0,v1
 0x58: lw      v1,12(t0)
 0x5c: lw      v0,0(v0)
 0x60: addu    a0,a0,v1
 0x64: sll     v0,v0,3
 0x68: addu    v0,v0,a1
 0x6c: lwc1    $f2,0(a0)
 0x70: lwc1    $f3,4(a0)
 0x74: lwc1    $f0,0(v0)
 0x78: lwc1    $f1,4(v0)
 0x7c: nop
 0x80: mul.d   $f2,$f2,$f0
 0x84: lwc1    $f0,0(t1)
 0x88: lwc1    $f1,4(t1)
 0x8c: nop
 0x90: add.d   $f0,$f0,$f2
 0x94: swc1    $f0,0(t1)
 0x98: swc1    $f1,4(t1)
 0x9c: lw      v0,20(t0)
 0xa0: nop
 0xa4: addu    v0,t2,v0
 0xa8: lw      v0,4(v0)
 0xac: addiu   a3,a3,1
 0xb0: slt     v0,a3,v0
 0xb4: bne     v0,zero,0x4c
 0xb8: sll     a0,a3,3

0x5c: lw      v0,0(v1)
0x60: lwc1    $f2,0(t0)
0x64: lwc1    $f3,4(t0)
0x68: sll     v0,v0,3
0x6c: addu    v0,v0,a1
0x70: lwc1    $f0,0(v0)
0x74: lwc1    $f1,4(v0)
0x78: nop
0x7c: mul.d   $f2,$f2,$f0
0x80: addiu   t0,t0,8
0x84: addiu   v1,v1,4
0x88: addiu   a3,a3,1
0x8c: slt     v0,a3,t2
0x90: bne     v0,zero,0x5c
0x94: add.d   $f4,$f4,$f2

0x48: lw      v0,0(v1)
0x4c: lwc1    $f2,0(t0)
0x50: lwc1    $f3,4(t0)
0x54: sll     v0,v0,3
0x58: addu    v0,v0,a1
0x5c: lwc1    $f0,0(v0)
0x60: lwc1    $f1,4(v0)
0x64: nop
0x68: mul.d   $f2,$f2,$f0
0x6c: addiu   v1,v1,4
0x70: addiu   t0,t0,8
0x74: sltu    v0,v1,a3
0x78: bne     v0,zero,0x48
0x7c: add.d   $f4,$f4,$f2

Figure 1: Optimizing C code

Statistics

Figure 2 shows the histogram of scores for Lab 1. The mean score was 69. The median score was 75. There were 6 perfect scores.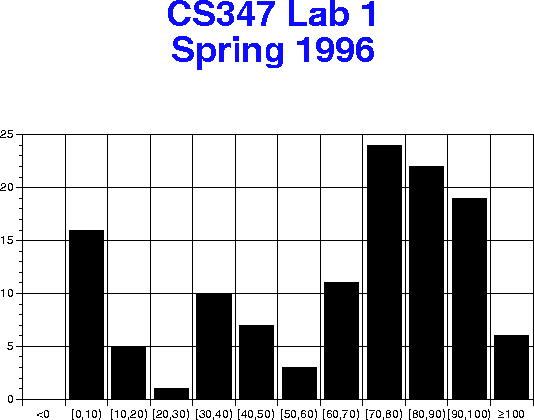

Figure 2: Lab 1 grades