Frequently Asked Questions

This is a list of some of the more specific frequently asked questions about the assignment. Please see also the roadmap if you have more general questions about how to approach the assignment.

Problems compiling the code under Linux

If you get an error like the following:

./ray: error while loading shared libraries: libboost_thread-gcc-mt-1_33_1.so.1.33.1: cannot open shared object file: No such file or directory

It means you need to set your $LD_LIBRARY_PATH to point to /afs/cs.cmu.edu/academic/class/15864-s05/lib/. Under csh, the command to do this is:

setenv LD_LIBRARY_PATH /afs/cs.cmu.edu/academic/class/15864-s05/lib/

Under bash, the command is:

export LD_LIBRARY_PATH=/afs/cs.cmu.edu/academic/class/15864-s05/lib/

Problems compiling the code under Windows

This program has a significant number of dependencies. To get everything working, please download:

An easier method is to just grab either photonMappingLibrariesWindowsVS71.zip or photonMappingLibrariesWindowsVS80.zip (depending on which version of Visual Studio you use); these should have everything you need.

This has been tested under Visual Studio 7.1 (a.k.a. VS2003) and Visual Studio 8 (a.k.a. VS2005). Previous versions of VS may work, since there's a lot of compatibility support there, but I can't make any promises.

If you experience the following warnings,

C:\boost_1_31_0\boost\thread\exceptions.hpp(29): warning C4275: non dll-interface class 'std::logic_error' used as base for dll-interface class 'boost::lock_error'

you can safely ignore these (at least according to this thread); to make them stop appearing go into the project settings, go under C/C++ -> Advanced and add "4275" to the "Disable Specific Warnings" box.

Do we need to worry about the specular component of the material?

No, for this assignment, you only need to worry about perfect mirror reflection (kr), diffuse reflection (kd), and refraction (kt). The sample solution samples the specular lobe as described in this document, but this is not required for the assignment.

How do I get the diffuse coefficient from a Material

The code was designed to allow for extensible (non-Phong) materials, so the Material class was made a virtual base class with the PhongMaterial class derived from it and containing the kd coefficient. This would allow for easy substitution of, e.g., the Torrence-Sparrow model should you so choose. This does present a difficulty, since you need to know things like the diffuse coefficient when reflecting photons. In the sample solution, I solved this by adding a virtual reflect method to the Material class and overriding it in PhongMaterial. If you choose not to do this, you are welcome to use dynamic_cast to cast from a Material* to a PhongMaterial* as follows, 

// Material* m defined previously
const PhongMaterial* pm = dynamic_cast<const PhongMaterial*>( m );
assert( pm != 0 );

How should we handle transparency, reflectivity, and the Fresnel equations?

Note: Henrik's book has an error in the Fresnel equations, please see his errata here before you implement!

A number of people have asked how the Fresnel term applies to the reflective sphere. Getting the correct Fresnel behavior for metals is fairly complex; for this assignment, you should just assume that the reflective sphere is purely reflective in the standard ray-tracing sense (i.e., always reflecting about the normal). You can either choose to always reflect a ray about its normal and add its contribution scaled by kr, or you can use the Russian roulette/path tracing approach and reflect a ray with probability kr and then add in its value unscaled.

Using the Fresnel term: At left, refraction without the Fresnel term; at right, the Fresnel term is used.

For the refractive sphere, you should be using the Fresnel term in the following way. Compute the portion of the light that is reflected using the Schlick approximation to the Fresnel equations for unpolarized light (recall that you can compute F_0 by simply plugging 0 in for the theta in the full Fresnel equations). Now, you can again use either Russian roulette or recursive ray tracing to determine what to do next, as above.

A simple description of the algorithm using a fully Russian roulette path tracing approach follows,

mu_0 = unif(0,1);
if( mu_0 < (kr) )
   Reflect a ray
else if( mu_0 < (kr + kt) )
   F_r = Fresnel term
   mu_1 = unif(0,1);
   if( mu_1 < F_r )
      Reflect a ray
   else
      Refract a ray
else if( mu_0 < (kr + kt + kd) )
   Diffusely scatter
else
   absorb

Why does the sample solution use the photon map estimate directly, rather than performing a final gather step as the assignment specifies

When the depth slider is set to 0, the sample solution will not cast any final gather rays. Fix this by setting depth to at least 1.

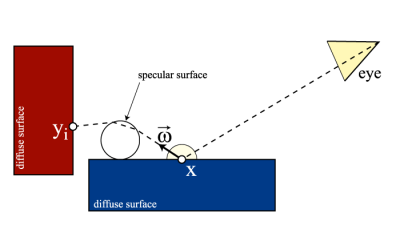
In the 2-pass algorithm, how do I use the photon map estimate for computing diffuse interreflection?

In our breakdown of the rendering equation, we have separated diffuse interreflection from the other parts (direct illumination, etc.). In some ways, this is the trickiest part to compute. We are going to use photon mapping to accelerate this in the following way, suggested by Henrik: once this ray hits another diffuse surface, we will take the irradiance estimate directly from the photon map, and not allow the ray to reflect any more.

There are some key points here:

Now that we have an estimate of the irradiance I(yi, yi → x), we can use this to estimate the contribution that diffuse-diffuse interreflection makes to the radiance I(x, x → eye). Note that in this case we must include an extra scaling factor of π, cancelling out the 1/π term in the diffuse BRDF; derivation of why this is can be found in this document.

Questions? Contact Christopher Twigg.