The second step in the analysis is to bound the probability that too
many packets pass through any switch in Steps 6
and 7. The following lemma provides
a bound on the probability that the congestion, c, in an M-input
butterfly exceeds 
in either of of these steps.
Proof: For the sake of brevity, we examine Step 7 only. A similar (and simpler) analysis holds for Step 6.
We begin by counting the number of packets that can possibly
use a switch. Let L denote the depth of an M-input butterfly,
i.e., 
. From a switch at level l, 
,
rows can be reached. The splitters partition these rows
into subbutterflies. By Lemma 8.4, the number of
packets that enter each of these subbutterflies is at most the number
of inputs, with high probability. Thus, at most 
packets can
pass through the switch.
Next we determine the probability that a packet that can pass
through the switch actually does so. A switch at level l can be
reached from 
different inputs. Since each packet begins in a
random input, the probability that it can reach the switch is
.
The number of packets, S, that pass through a particular
switch at level l has a binomial distribution. The number of trials
is 
and the probability of success is 
.
Thus,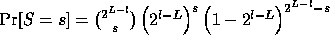 
and
.
Using the inequality 
, we have 
.
We bound the congestion in the entire butterfly by summing the
individual probabilities over all 
switches in the
butterfly. We have
For 
, we have 
for some constant 
.
