Triangle generates a conforming constrained Delaunay triangulation whenever the -q, -a, or -u, switch is used. These switches set constraints on angles and triangle sizes in the mesh.

The -q switch sets a minimum angle constraint. A number may follow the `q'; otherwise, the default minimum angle is twenty degrees. For the vertex set spiral.node below, consider the differences among

triangle spiral
triangle -q spiral
triangle -q32.5 spiral

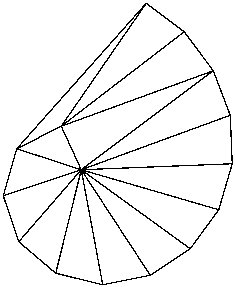
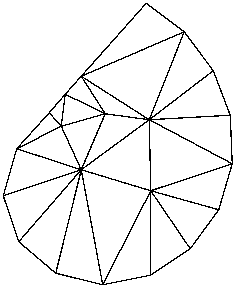
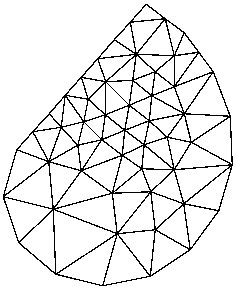
Note that the angle constraint does not apply to small angles between input segments; such angles cannot be removed.

The -a switch sets a maximum area constraint. There are three ways to use this switch. The first way is to specify a maximum area on the command line. The next example is a mesh in which no triangle has area greater than 0.2.

triangle -a.2 spiral

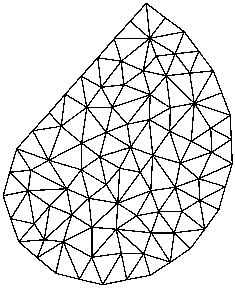
The second manner of using the -a switch is applicable only when creating a new mesh from a PSLG. The file describing the PSLG itself contains area constraints, each of which is applied to a segment-bounded region; see the .poly file format for details. For an example, look at the last seven lines of la.poly, which describes a vertical cross section of soil in the Los Angeles Basin. Below is an illustration of the results when the -a switch is or is not invoked.

triangle -pq la
triangle -pqa la

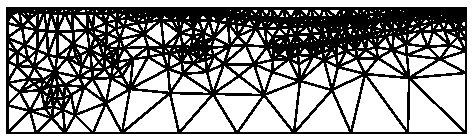
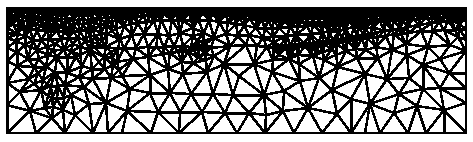
The third manner is applicable only when refining a preexisting mesh. See the refinement page for details.

The -u switch imposes a user-defined constraint on triangle size. There are two ways to use this feature. One is to edit the triunsuitable() procedure in triangle.c to encode any constraint you like, then recompile Triangle. The other is to compile triangle.c with the EXTERNAL_TEST symbol set (compiler switch -DEXTERNAL_TEST), then link Triangle against a separate object file that implements triunsuitable(). In either case, the -u switch causes the user-defined test to be applied to every triangle.

A few applications, such as some finite volume methods, may have an extra requirement: the mesh must be a conforming Delaunay triangulation - meaning that every triangle is truly Delaunay (not just constrained Delaunay) - and the center of each triangle's circumcircle must lie within the triangulation. This requirement arises because the Voronoi diagram, found by dualizing the Delaunay triangulation, must intersect ``nicely'' with the triangulation. If your application has this requirement, use the -D switch to ensure that the mesh is conforming Delaunay.