•
Quantized
EDF Scheduling
Worst
Case Analysis with Unknown Deadline Distribution
When the deadline distribution is unknown, we performed a worst case analysis
where only the following four parameters are known:
 |
First two moments of incoming tasks |
|
Deadline range
(R=Dmax-Dmin) and average deadline |
We found that:
|
Uniform partitioning is also optimal against worst case deadline distribution |
|
The
lateness ratio of Q-EDF to EDF is bounded by an expression involving
traffic parameter and deadline range R. |
|
For
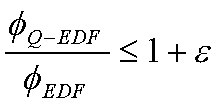 , K priority
levels are needed where  |
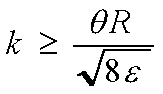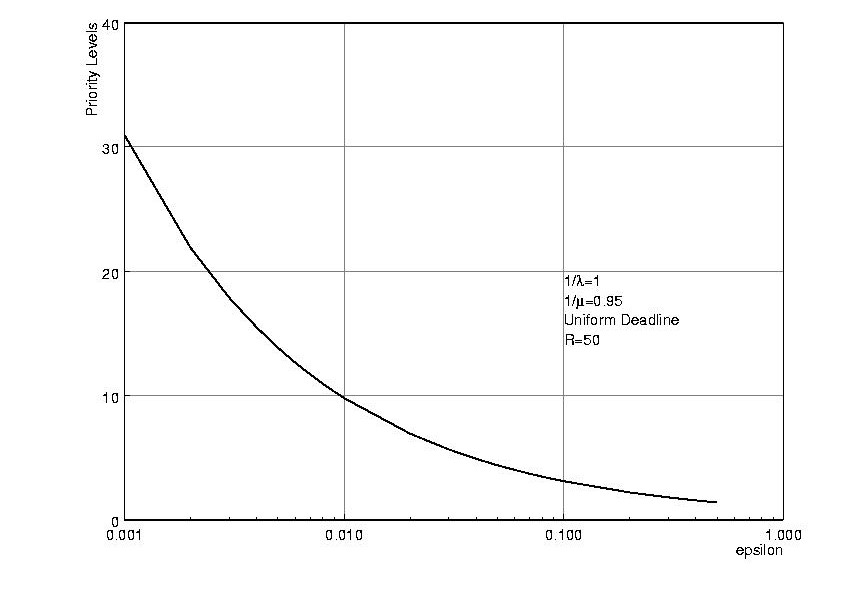
This is a comparison of logarithmic partitioning and uniform partitioning.
This figure shows the priority levels needed for different e. It
can be seen that when
e = 0.02, deadline range is 50, k only needs to be >= 6.9 where three bits are enough.
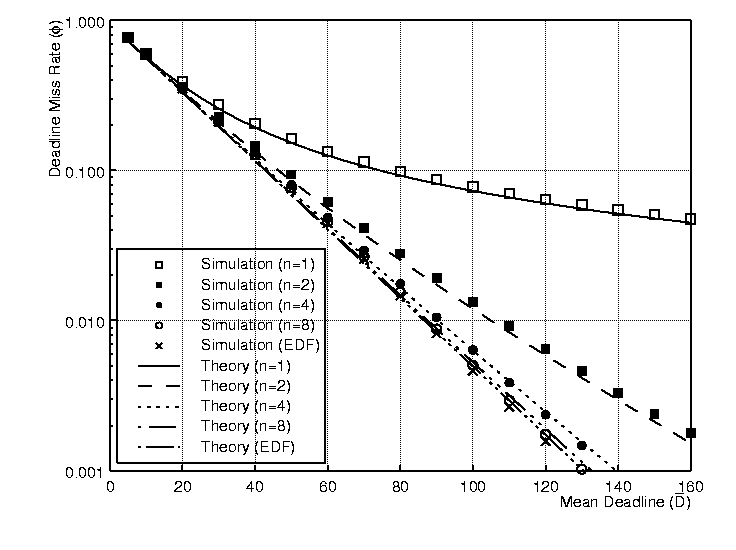
Q-MARS
