Given a normalized spanning intervals 
, its complement 
is a set of normalized spanning intervals whose extension is
the complement of the extension of .
One can compute as follows:
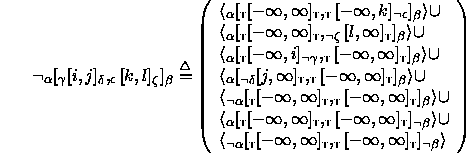
An important property of normalized spanning intervals is that for any
normalized spanning interval , contains at most seven
normalized spanning intervals.
The intuition behind the above definition is as follows.
First note that the negation of 
is
.
Next note that the extension of contains intervals whose endpoints q
and r satisfy
.
Thus the extension of contains intervals whose endpoints satisfy the
negation of this, namely
.
Such a disjunction requires four spanning intervals, the first four in the
above definition.
Additionally, if the extension of contains intervals of the form [q,r],
the extension of will contain all intervals not of the form [q,r],
namely (q,r], [q,r), and (q,r).
Similarly for the cases where the extension of contains intervals of the
form (q,r], [q,r), or (q,r).
This accounts for the last three spanning intervals in the above definition.
We now see why it is necessary to allow spanning intervals to have open ranges
of endpoint values as well as infinite endpoints.
The complement of a spanning interval, such as [[i,j],[k,l]], with closed
endpoint ranges and finite endpoints includes spanning intervals, such as
, with open endpoint ranges and infinite
endpoints.