- ... function1
- Some authors also use the term scoring metric.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nodes2
- For reasons of simplicity, the set of nodes which are in one-to-one correspondence with the variables in
 will also be denoted by
will also be denoted by  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...equivalent3
- Several authors also use the term independence equivalent, and reserve the term distribution equivalent (wrt some family of distributions
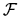 ) for the more restricted case where the two DAGs can represent the same probability distributions. In the common situation where all the variables are discrete and
) for the more restricted case where the two DAGs can represent the same probability distributions. In the common situation where all the variables are discrete and 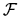 is the family of unrestricted multinomial distributions, these two concepts of equivalence coincide.
is the family of unrestricted multinomial distributions, these two concepts of equivalence coincide.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... classes4
- Note that the operators of addition and reversal of an arc in the DAG space also need a consistency check, but in this case we simply test the absence of directed cycles.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... component5
- A chain component of
 is any connected component of the undirected graph obtained from
is any connected component of the undirected graph obtained from  by removing all the arcs.
by removing all the arcs.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...arb_stats6
- This tree could be organized differently in order to improve the efficiency in the location of the current state. However, this particular tree was selected so as to clarify the presentation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Chickering027
- This work appeared after the original submission of this paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.