The Learning Algorithm

Having described how we set up the learning problem, we are now ready to describe the learning algorithm that we used. Briefly, we solved this learning problem by first reducing to a multiclass, multi-label classification problem (or alternatively a multiple logistic regression problem), and then applying boosting techniques developed by Schapire and Singer SchapireSi99,SchapireSi00 combined with a modification of boosting algorithms for logistic regression proposed by Collins, Schapire and Singer CollinsScSi02. The result is a new machine-learning algorithm for solving conditional density estimation problems, described in detail in the remainder of this section. Table 5 shows pseudo-code for the entire algorithm.

Table 5: The boosting-based algorithm for conditional density estimation.

Abstractly, we are given pairs $(x_1,y_1),\ldots,(x_m,y_m)$ where each $x_i$ belongs to a space $X$ and each $y_i$ is in $\mbox{\msym R}$. In our case, the $x_i$'s are the auction-specific feature vectors described above; for some $n$, $X\subseteq (\mbox{\msym R}\cup \{\perp \})^n$. Each target quantity $y_i$ is the difference between closing price and current price. Given a new $x$, our goal is to estimate the conditional distribution of $y$ given $x$.

We proceed with the working assumption that all training and test examples $(x,y)$ are i.i.d. (i.e, drawn independently from identical distributions). Although this assumption is false in our case (since the agents, including ours, are changing over time), it seems like a reasonable approximation that greatly reduces the difficulty of the learning task.

Our first step is to reduce the estimation problem to a classification problem by breaking the range of the $y_i$'s into bins:

$$[b_0,b_1), [b_1,b_2), \ldots, [b_k,b_{k+1}]$$

for some breakpoints $b_0 < b_1 < \cdots < b_k \leq b_{k+1}$ where for our problem, we chose $k=50$.⁷ The endpoints $b_0$ and $b_{k+1}$ are chosen to be the smallest and largest $y_i$ values observed during training. We choose the remaining breakpoints $b_1,\ldots,b_k$ so that roughly an equal number of training labels $y_i$ fall into each bin. (More technically, breakpoints are chosen so that the entropy of the distribution of bin frequencies is maximized.)

For each of the breakpoints $b_j$ ($j=1,\ldots,k$), our learning algorithm attempts to estimate the probability that a new $y$ (given $x$) will be at least $b_j$. Given such estimates $p_j$ for each $b_j$, we can then estimate the probability that $y$ is in the bin $[b_j,b_{j+1})$ by $p_{j+1}-p_j$ (and we can then use a constant density within each bin). We thus have reduced the problem to one of estimating multiple conditional Bernoulli variables corresponding to the event $y\geq b_j$, and for this, we use a logistic regression algorithm based on boosting techniques as described by CollinsScSi02 CollinsScSi02.

Our learning algorithm constructs a real-valued function $f:X\times \{1,\ldots,k\} \rightarrow \mbox{\msym R}$ with the interpretation that

$$\frac{1}{1 + \exp(-f(x,j))}$$ (9)

is our estimate of the probability that $y\geq b_j$, given $x$. The negative log likelihood of the conditional Bernoulli variable corresponding to $y_i$ being above or below $b_j$ is then

$$\ln\left({1 + e^{- s_j(y_i) f(x_i, j)}}\right)$$

where

$$s_j(y) = \left\{ \begin{array}{ll} +1 & \mbox{if $y \geq b_j$} \\ -1 & \mbox{if $y < b_j$.} \end{array} \right.$$ (10)

We attempt to minimize this quantity for all training examples $(x_i,y_i)$ and all breakpoints $b_j$. Specifically, we try to find a function $f$ minimizing

$$\sum_{i=1}^m \sum_{j=1}^k \ln\left({1 + e^{- s_j(y_i) f(x_i, j)}}\right).$$

We use a boosting-like algorithm described by CollinsScSi02 CollinsScSi02 for minimizing objective functions of exactly this form. Specifically, we build the function $f$ in rounds. On each round $t$, we add a new base function $h_t: X \times \{1,\ldots,k\}\rightarrow \mbox{\msym R}$. Let

$$f_t = \sum_{t' = 1}^{t-1} h_{t'}$$

be the accumulating sum. Following Collins, Schapire and Singer, to construct each $h_t$, we first let

$$W_t(i,j) = \frac{1}{1+e^{s_j(y_i) f_t(x_i,j)}}$$

be a set of weights on example-breakpoint pairs. We then choose $h_t$ to minimize

$$\sum_{i=1}^m \sum_{j=1}^k W_t(i,j) e^{- s_j(y_i) h_t(x_i, j)}$$ (11)

over some space of ``simple'' base functions $h_t$. For this work, we considered all ``decision stumps'' $h$ of the form

$$h(x,j) = \left\{ \begin{array}{ll} A_j & \mbox{if $\phi(... ...} \\ C_j & \mbox{if $\phi(x) = \perp $} \end{array} \right.$$

where $\phi(\cdot)$ is one of the features described above, and $\theta$, $A_j$, $B_j$ and $C_j$ are all real numbers. In other words, such an $h$ simply compares one feature $\phi$ to a threshold $\theta$ and returns a vector of numbers $h(x,\cdot)$ that depends only on whether $\phi(x)$ is unknown ($\perp$), or above or below $\theta$. SchapireSi00 SchapireSi00 show how to efficiently search for the best such $h$ over all possible choices of $\phi$, $\theta$, $A_j$, $B_j$ and $C_j$. (We also employed their technique for ``smoothing'' $A_j$, $B_j$ and $C_j$.)

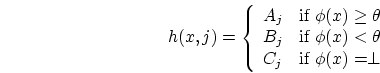
When computed by this sort of iterative procedure, CollinsScSi02 CollinsScSi02 prove the asymptotic convergence of $f_t$ to the minimum of the objective function in Equation (11) over all linear combinations of the base functions. For this problem, we fixed the number of rounds to $T=300$. Let $f=f_{T+1}$ be the final predictor.

As noted above, given a new feature vector $x$, we compute $p_j$ as in Equation (9) to be our estimate for the probability that $y\geq b_j$, and we let $p_0 = 1$ and $p_{k+1}=0$. For this to make sense, we need $p_1\geq p_2\geq \cdots \geq p_k$, or equivalently, $f(x,1)\geq f(x,2)\geq \cdots \geq f(x,k)$, a condition that may not hold for the learned function $f$. To force this condition, we replace $f$ by a reasonable (albeit heuristic) approximation $f'$ that is nonincreasing in $j$, namely, $f' = (\overline{f}+ \underline{f}) / 2$ where $\overline{f}$ (respectively, $\underline{f}$) is the pointwise minimum (respectively, maximum) of all nonincreasing functions $g$ that everywhere upper bound $f$ (respectively, lower bound $f$).

With this modified function $f'$, we can compute modified probabilities $p_j$. To sample a single point according to the estimated distribution on $\mbox{\msym R}$ associated with $f'$, we choose bin $[b_j,b_{j+1})$ with probability $p_j - p_{j+1}$, and then select a point from this bin uniformly at random. Expected value according to this distribution is easily computed as

$$\sum_{j=0}^k (p_j - p_{j+1}) \left({\frac{b_{j+1} + b_j}{2}}\right).$$

Although we present results using this algorithm in the trading agent context, we did not test its performance on more general learning problems, nor did we compare to other methods for conditional density estimation, such as those studied by Stone94 Stone94. This clearly should be an area for future research.