Results of the Statistical Study

Table 9: Significant levels, $\alpha ^*$, of each term of the linear model, determination coefficient $R^2$, and value of Levene test of the statistical analysis of CIXL2 parameters.

Function	$\mathbf{\alpha^*}$ C	$\mathbf{\alpha^*}$ B	$\mathbf{\alpha^*}$ CB	$\mathbf{R^2}$	$\mathbf{\alpha^*}$ T. Levene
$f_{Sph}$	1.000	1.000	---	---	0.000
$f_{SchDS}$	0.000	0.000	0.000	0.601	0.000
$f_{Ros}$	0.005	0.000	0.006	0.526	0.000
$f_{Ras}$	0.000	0.000	0.000	0.617	0.000
$f_{Sch}$	0.000	0.000	0.000	0.805	0.000
$f_{Ack}$	0.095	0.000	0.019	0.083	0.000
$f_{Gri}$	0.149	0.001	---	0.040	0.000
$f_{Fle}$	0.410	0.000	---	0.054	0.003
$f_{Lan}$	0.040	0.000	0.024	0.159	0.000

Table 10: Significance level of the crossover operator and determination coefficient $R^2$ of the linear model, and value of Levene test of the comparative study of the crossovers.

Function	$\mathbf{\alpha^*}$ Crossover	$\mathbf{R^2}$	$\mathbf{\alpha^*}$ Levene test
$f_{Sph}$	0.000	0.779	0.000
$f_{SchDS}$	0.000	0.786	0.000
$f_{Ros}$	0.573	0.024	0.000
$f_{Ras}$	0.000	0.971	0.000
$f_{Sch}$	0.000	0.987	0.000
$f_{Ack}$	0.000	0.884	0.000
$f_{Gri}$	0.000	0.421	0.000
$f_{Fle}$	0.000	0.137	0.091
$f_{Lan}$	0.000	0.486	0.000

Table 11: Significance level of the evolutionary algorithms and determination coefficient $R^2$ of the linear model, and value of Levene test of the comparative study betwen CIXL2 and EDAs.

Function	$\mathbf{\alpha^*}$ EA	$\mathbf{R^2}$	$\mathbf{\alpha^*}$ Levene test
$f_{SchDS}$	0.000	0.955	0.000
$f_{Ros}$	0.000	0.778	0.000
$f_{Ras}$	0.000	0.992	0.000
$f_{Sch}$	0.000	0.999	0.000
$f_{Ack}$	1.000	0.641	1.000
$f_{Gri}$	0.000	0.455	0.000
$f_{Fle}$	0.001	0.150	0.000
$f_{Lan}$	0.027	0.079	0.000

Table 12: Results for all the functions of the multiple comparison test and the ranking obtained depending on the number of best individuals $n$.

$\mathbf{I}$	$\mathbf{J}$		$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$
			$\mathbf{f_{Sph}}$				$\mathbf{f_{SchDS}}$				$\mathbf{f_{Ros}}$
5	10		-2.683e-15	0.000			-2.540e-02	0.000			-9.433e-01	0.000
	30		-4.144e-11	0.000			-1.899e-01	0.000			-1.486e+00	0.000
	60		-1.836e-07	0.000			-2.371e-01	0.000			-1.058e+00	0.000
	90		-5.554e-08	0.000			-1.004e+00	0.000			-8.375e-01	0.000
10	5		2.683e-15	0.000			2.540e-02	0.000			9.433e-01	0.000
	30		-4.144e-11	0.000			-1.645e-01	0.000			-5.425e-01	0.000
	60		-1.836e-07	0.000			-2.117e-01	0.000			-1.142e-01	0.025
	90		-5.554e-08	0.000			-9.785e-01	0.000			1.058e-01	0.014
30	5		4.144e-11	0.000			1.899e-01	0.000			1.486e+00	0.000
	10		4.144e-11	0.000			1.645e-01	0.000			5.425e-01	0.000
	60		-1.835e-07	0.000			-4.720e-02	0.572			4.283e-01	0.000
	90		-5.549e-08	0.000			-8.140e-01	0.000			6.483e-01	0.000
60	5		1.836e-07	0.000			2.371e-01	0.000			1.058e+00	0.000
	10		1.836e-07	0.000			2.117e-01	0.000			1.142e-01	0.025
	30		1.835e-07	0.000			4.720e-02	0.572			-4.283e-01	0.000
	90		1.281e-07	0.003			-7.668e-01	0.000			2.200e-01	0.000
90	5		5.554e-08	0.000			1.004e+00	0.000			8.375e-01	0.000
	10		5.554e-08	0.000			9.785e-01	0.000			-1.058e-01	0.014
	30		5.549e-08	0.000			8.140e-01	0.000			-6.483e-01	0.000
	60		-1.281e-07	0.003			7.668e-01	0.000			-2.200e-01	0.000
Ranking		$\mu_{60}>\mu_{90}>\mu_{30}>\mu_{10}>\mu_{5}$				$\mu_{90}>\mu_{30}>\mu_{10}>\mu_{5}$				$\mu_{30}>\mu_{60}>\mu_{10}>\mu_{90}>\mu_{5}$
						$\mu_{60}>\mu_{5}$
			$\mathbf{f_{Ras}}$				$\mathbf{f_{Sch}}$				$\mathbf{f_{Ack}}$
5	10		-5.79e+00	0.000			-2.691e+02	0.082			-1.063e-07	0.000
	30		-6.72e+00	0.000			-7.338e+02	0.000			-2.384e-05	0.000
	60		-1.01e+01	0.000			-9.559e+02	0.000			-1.508e-03	0.000
	90		-1.51e+01	0.000			-1.148e+03	0.000			-6.769e-02	0.216
10	5		5.79e+00	0.000			2.691e+02	0.082			1.063e-07	0.000
	30		-9.31e-01	0.807			-4.647e+02	0.000			-2.373e-05	0.000
	60		-4.30e+00	0.000			-6.868e+02	0.000			-1.508e-03	0.000
	90		-9.32e+00	0.000			-8.786e+02	0.000			-6.769e-02	0.216
30	5		6.72e+00	0.000			7.338e+02	0.000			2.384e-05	0.000
	10		9.31e-01	0.807			4.647e+02	0.000			2.373e-05	0.000
	60		-3.37e+00	0.000			-2.221e+02	0.000			-1.484e-03	0.000
	90		-8.39e+00	0.000			-4.139e+02	0.000			-6.767e-02	0.216
60	5		1.01e+01	0.000			9.559e+02	0.000			1.508e-03	0.000
	10		4.30e+00	0.000			6.868e+02	0.000			1.508e-03	0.000
	30		3.37e+00	0.000			2.221e+02	0.000			1.484e-03	0.000
	90		-5.02e+00	0.000			-1.918e+02	0.000			-6.619e-02	0.242
90	5		1.51e+01	0.000			1.148e+03	0.000			6.769e-02	0.216
	10		9.32e+00	0.000			8.786e+02	0.000			6.769e-02	0.216
	30		8.39e+00	0.000			4.139e+02	0.000			6.767e-02	0.216
	60		5.02e+00	0.000			1.918e+02	0.000			6.619e-02	0.242
Ranking		$\mu_{90}>\mu_{60}>\mu_{10}>\mu_{5}$				$\mu_{90}>\mu_{60}>\mu_{30}>\mu_{5}$				$\mu_{60}>\mu_{30}>\mu_{10}>\mu_{5}$
		$\mu_{30}>\mu_{5}$				$\mu_{10}\ge\mu_{5}$				$\mu_{90}\ge\mu_{5}$
			$\mathbf{f_{Gri}}$				$\mathbf{f_{Fle}}$				$\mathbf{f_{Lan}}$
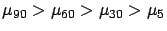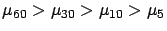5	10		-7.207E-03	0.174			-2.776e+03	0.885			-1.354e-02	0.998
	30		-3.896E-03	0.864			-7.968e+03	0.004			-5.881e-02	0.009
	60		2.329E-03	1.000			-7.342e+03	0.008			-8.794e-02	0.000
	90		8.649E-03	0.001			-1.268e+04	0.000			-1.142e-01	0.000
10	5		7.207E-03	0.174			2.776e+03	0.885			1.354e-02	0.998
	30		3.311E-03	0.983			-5.192e+03	0.234			-4.527e-02	0.082
	60		9.535E-03	0.533			-4.566e+03	0.378			-7.440e-02	0.000
	90		1.586E-02	0.000			-9.899e+03	0.006			-1.007e-01	0.000
30	5		3.896E-03	0.864			7.968e+03	0.004			5.881e-02	0.009
	10		-3.311E-03	0.983			5.192e+03	0.234			4.527e-02	0.082
	60		6.225E-03	0.930			6.254e+02	1.000			-2.913e-02	0.354
	90		1.254E-02	0.000			-4.707e+03	0.678			-5.540e-02	0.000
60	5		-2.329E-03	1.000			7.342e+03	0.008			8.794e-02	0.000
	10		-9.535E-03	0.533			4.566e+03	0.378			7.440e-02	0.000
	30		-6.225E-03	0.930			-6.254e+02	1.000			2.913e-02	0.354
	90		6.320E-03	0.884			-5.333e+03	0.491			-2.627e-02	0.247
90	5		-8.649E-03	0.001			1.268e+04	0.000			1.142e-01	0.000
	10		-1.586E-02	0.000			9.899e+03	0.006			1.007e-01	0.000
	30		-1.254E-02	0.000			4.707e+03	0.678			5.540e-02	0.000
	60		-6.320E-03	0.884			5.333e+03	0.491			2.627e-02	0.247
Ranking		$\mu_{60}\ge\mu_{90} \ \ \ \ \ \mu_{5}>\mu_{90}$				$\mu_{10}\ge\mu_{5} \ \ \ \ \ \mu_{30}>\mu_{5}$				$\mu_{10}\ge\mu_{5} \ \ \ \ \ \mu_{30}>\mu_{5}$
		$\mu_{10}>\mu_{90} \ \ \ \ \ \mu_{30}>\mu_{90}$				$\mu_{60}>\mu_{5} \ \ \ \ \ \mu_{90}>\mu_{5}$				$\mu_{60}>\mu_{5} \ \ \ \ \ \mu_{90}>\mu_{5}$

Table 13: Results for all the functions of the multiple comparison test and the ranking obtained depending on the confidence coefficient $1-\alpha$.

$\mathbf{I}$	$\mathbf{J}$		$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$
			$\mathbf{f_{Sph}}$				$\mathbf{f_{SchDS}}$				$\mathbf{f_{Ros}}$
0.70	0.90		-1.361e-08	0.000			-3.985e-01	0.000			-1.360e-01	0.281
	0.95		-4.394e-08	0.000			-3.783e-02	0.967			-1.693e-01	0.131
	0.99		-1.302e-07	0.000			8.165e-02	0.114			-1.813e-01	0.310
0.90	0.70		1.361e-08	0.000			3.985e-01	0.000			1.360e-01	0.281
	0.95		-3.033e-08	0.000			3.607e-01	0.001			-3.333e-02	0.995
	0.99		-1.166e-07	0.000			4.802e-01	0.000			-4.533e-02	0.996
0.95	0.70		4.394e-08	0.000			3.783e-02	0.967			1.693e-01	0.131
	0.90		3.033e-08	0.000			-3.607e-01	0.001			3.333e-02	0.995
	0.99		-8.628e-08	0.019			1.195e-01	0.013			-1.200e-02	1.000
0.99	0.70		1.302e-07	0.000			-8.165e-02	0.114			1.813e-01	0.310
	0.90		1.166e-07	0.000			-4.802e-01	0.000			4.533e-02	0.996
	0.95		8.628e-08	0.019			-1.195e-01	0.013			1.200e-02	1.000
Ranking		$\mu_{0.99}>\mu_{0.95}>\mu_{0.90}>\mu_{0.70}$				$\mu_{0.90}>\mu_{0.95}>\mu_{0.99}$				$\mu_{0.99}\ge\mu_{0.95}\ge\mu_{0.90}\ge\mu_{0.70}$
						$\mu_{0.70}\ge\mu_{0.99}$
			$\mathbf{f_{Ras}}$				$\mathbf{f_{Sch}}$				$\mathbf{f_{Ack}}$
0.70	0.90		-4.23e+00	0.000			1.198e+02	0.714			-2.471e-04	0.000
	0.95		-3.59e+00	0.000			8.247e+01	0.919			-1.944e-02	0.617
	0.99		-5.56e+00	0.000			-3.008e+02	0.001			-3.541e-02	0.382
0.90	0.70		4.23e+00	0.000			-1.198e+02	0.714			2.471e-04	0.000
	0.95		6.40e-01	0.966			-3.736e+01	0.997			-1.919e-02	0.631
	0.99		-1.33e+00	0.551			-4.206e+02	0.000			-3.516e-02	0.390
0.95	0.70		3.59e+00	0.000			-8.247e+01	0.919			1.944e-02	0.617
	0.90		-6.40e-01	0.966			3.736e+01	0.997			1.919e-02	0.631
	0.99		-1.97e+00	0.044			-3.833e+02	0.000			-1.597e-02	0.985
0.99	0.70		5.56e+00	0.000			3.008e+02	0.001			3.541e-02	0.382
	0.90		1.33e+00	0.551			4.206e+02	0.000			3.516e-02	0.390
	0.95		1.97e+00	0.044			3.833e+02	0.000			1.597e-02	0.985
Ranking		$\mu_{0.99}>\mu_{0.95}>\mu_{0.70}$				$\mu_{0.70}\ge\mu_{0.95}\ge\mu_{0.90}$				$\mu_{0.99}\ge\mu_{0.95}\ge\mu_{0.70}$
		$\mu_{0.90}>\mu_{0.70}$				$\mu_{0.99}>\mu_{0.90}$				$\mu_{0.90}>\mu_{0.70}$
			$\mathbf{f_{Gri}}$				$\mathbf{f_{Fle}}$				$\mathbf{f_{Lan}}$
0.70	0.90		-7.196E-03	0.395			-2.986e+03	0.717			6.105e-03	0.998
	0.95		-2.027E-03	0.945			-3.241e+03	0.635			2.867e-02	0.272
	0.99		-5.667E-03	0.155			-3.079e+03	0.644			3.309e-02	0.133
0.90	0.70		7.196E-03	0.395			2.986e+03	0.717			-6.105e-03	0.998
	0.95		5.168E-03	0.791			-2.547e+02	1.000			2.257e-02	0.585
	0.99		1.529E-03	1.000			-9.255e+01	1.000			2.698e-02	0.363
0.95	0.70		2.027E-03	0.945			3.241e+03	0.635			-2.867e-02	0.272
	0.90		-5.168E-03	0.791			2.547e+02	1.000			-2.257e-02	0.585
	0.99		-3.640E-03	0.747			1.622e+02	1.000			4.415e-03	1.000
0.99	0.70		5.667E-03	0.155			3.079e+03	0.644			-3.309e-02	0.133
	0.90		-1.529E-03	1.000			9.255e+01	1.000			-2.698e-02	0.363
	0.95		3.640E-03	0.747			-1.622e+02	1.000			-4.415e-03	1.000
Ranking		$\mu_{0.90}\ge\mu_{0.99}\ge\mu_{0.95}\ge\mu_{0.70}$				$\mu_{0.95}\ge\mu_{0.99}\ge\mu_{0.90}\ge\mu_{0.70}$				$\mu_{0.70}\ge\mu_{0.90}\ge\mu_{0.95}\ge\mu_{0.99}$

Table 14: Results of the multiple comparison tests for $f_{Sph}$, $f_{SchDS}$ y $f_{Ros}$ functions and the ranking established by the test regarding the crossover operator.

Crossover		$\mathbf{f_{Sph}}$				$\mathbf{f_{SchDS}}$				$\mathbf{f_{Ros}}$
I	J	$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$
CIXL2	BLX(0.3)	3.109e-16	0.000			-1.583e-02	0.000			-4.283e+00	0.997
	BLX(0.5)	1.628e-16	0.212			-7.337e-03	0.028			-6.667e+00	0.933
	SBX(2)	-1.644e-12	0.000			-2.014e-01	0.000			-2.809e+00	0.958
	SBX(5)	-4.873e-12	0.000			-3.913e-01	0.000			-6.165e+00	0.944
	Fuzzy	-2.102e-15	0.000			-3.968e+01	0.000			-2.487e+00	1.000
	Logical	-3.689e-13	0.000			-1.098e+01	0.000			-2.092e+00	0.000
	UNDX	-2.910e-05	0.000			-2.080e+01	0.000			-3.460e+00	0.000
BLX(0.3)	CIXL2	-3.109e-16	0.000			1.583e-02	0.000			4.283e+00	0.997
	BLX(0.5)	-1.480e-16	0.074			8.495e-03	0.357			-2.384e+00	1.000
	SBX(2)	-1.644e-12	0.000			-1.855e-01	0.000			1.473e+00	1.000
	SBX(5)	-4.873e-12	0.000			-3.755e-01	0.000			-1.882e+00	1.000
	Fuzzy	-2.413e-15	0.000			-3.966e+01	0.000			1.796e+00	1.000
	Logical	-3.692e-13	0.000			-1.097e+01	0.000			2.191e+00	1.000
	UNDX	-2.910e-05	0.000			-2.078e+01	0.000			8.225e-01	1.000
BLX(0.5)	CIXL2	-1.628e-16	0.212			7.337e-03	0.028			6.667e+00	0.933
	BLX(0.3)	1.480e-16	0.074			-8.495e-03	0.357			2.384e+00	1.000
	SBX(2)	-1.644e-12	0.000			-1.940e-01	0.000			3.857e+00	1.000
	SBX(5)	-4.873e-12	0.000			-3.840e-01	0.000			5.019e-01	1.000
	Fuzzy	-2.265e-15	0.000			-3.967e+01	0.000			4.179e+00	1.000
	Logical	-3.690e-13	0.000			-1.098e+01	0.000			4.575e+00	1.000
	UNDX	-2.910e-05	0.000			-2.079e+01	0.000			3.206e+00	1.000
SBX(2)	CIXL2	1.644e-12	0.000			2.014e-01	0.000			2.809e+00	0.958
	BLX(0.3)	1.644e-12	0.000			1.855e-01	0.000			-1.473e+00	1.000
	BLX(0.5)	1.644e-12	0.000			1.940e-01	0.000			-3.857e+00	1.000
	SBX(5)	-3.229e-12	0.000			-1.900e-01	0.115			-3.355e+00	1.000
	Fuzzy	1.642e-12	0.000			-3.948e+01	0.000			3.222e-01	1.000
	Logical	1.275e-12	0.000			-1.078e+01	0.000			7.179e-01	1.000
	UNDX	-2.910e-05	0.000			-2.060e+01	0.000			-6.508e-01	1.000
SBX(5)	CIXL2	4.873e-12	0.000			3.913e-01	0.000			6.165e+00	0.944
	BLX(0.3)	4.873e-12	0.000			3.755e-01	0.000			1.882e+00	1.000
	BLX(0.5)	4.873e-12	0.000			3.840e-01	0.000			-5.019e-01	1.000
	SBX(2)	3.229e-12	0.000			1.900e-01	0.115			3.355e+00	1.000
	Fuzzy	4.871e-12	0.000			-3.929e+01	0.000			3.678e+00	1.000
	Logical	4.504e-12	0.000			-1.059e+01	0.000			4.073e+00	1.000
	UNDX	-2.910e-05	0.000			-2.041e+01	0.000			2.705e+00	1.000
Fuzzy	CIXL2	2.102e-15	0.000			3.968e+01	0.000			2.487e+00	1.000
	BLX(0.3)	2.413e-15	0.000			3.966e+01	0.000			-1.796e+00	1.000
	BLX(0.5)	2.265e-15	0.000			3.967e+01	0.000			-4.179e+00	1.000
	SBX(2)	-1.642e-12	0.000			3.948e+01	0.000			-3.222e-01	1.000
	SBX(5)	-4.871e-12	0.000			3.929e+01	0.000			-3.678e+00	1.000
	Logical	-3.668e-13	0.000			2.870e+01	0.000			3.957e-01	1.000
	UNDX	-2.910e-05	0.000			1.888e+01	0.000			-9.730e-01	1.000
Logical	CIXL2	3.689e-13	0.000			1.098e+01	0.000			2.092e+00	0.000
	BLX(0.3)	3.692e-13	0.000			1.097e+01	0.000			-2.191e+00	1.000
	BLX(0.5)	3.690e-13	0.000			1.098e+01	0.000			-4.575e+00	1.000
	SBX(2)	-1.275e-12	0.000			1.078e+01	0.000			-7.179e-01	1.000
	SBX(5)	-4.504e-12	0.000			1.059e+01	0.000			-4.073e+00	1.000
	Fuzzy	3.668e-13	0.000			-2.870e+01	0.000			-3.957e-01	1.000
	UNDX	-2.910e-05	0.000			-9.812e+00	0.000			-1.369e+00	0.000
UNDX	CIXL2	2.910e-05	0.000			2.080e+01	0.000			3.460e+00	0.000
	BLX(0.3)	2.910e-05	0.000			2.078e+01	0.000			-8.225e-01	1.000
	BLX(0.5)	2.910e-05	0.000			2.079e+01	0.000			-3.206e+00	1.000
	SBX(2)	2.910e-05	0.000			2.060e+01	0.000			6.508e-01	1.000
	SBX(5)	2.910e-05	0.000			2.041e+01	0.000			-2.705e+00	1.000
	Fuzzy	2.910e-05	0.000			-1.888e+01	0.000			9.730e-01	1.000
	Logical	2.910e-05	0.000			9.812e+00	0.000			1.369e+00	0.000
Function	Ranking
$f_{Sph}$	$\mu_{UNDX} > \mu_{SBX(5)} > \mu_{SBX(2)} > \mu_{Logical} > \mu_{Ext.F.} > \mu_{CIXL2} \ge \mu_{BLX(0.5)} \ge \mu_{BLX(0.3)}$
$f_{SchDS}$	$\mu_{Ext.F.} > \mu_{UNDX} > \mu_{Logical} > \mu_{SBX(5)} \ge \mu_{SBX(2)} > \mu_{BLX(0.3)} \ge \mu_{BLX(0.5)} > \mu_{CIXL2}$
$f_{Ros}$	$\mu_{BLX(0.5)} \ge \mu_{SBX(5)} \ge \mu_{BLX(0.3)} \ge \mu_{UNDX} \ge \mu_{SBX(2)} \ge \mu_{Ext.F.} \ge \mu_{Logical} > \mu_{CIXL2}$

Table 15: Results of the multiple comparison tests for $f_{Ras}$, $f_{Sch}$ and $f_{Ack}$ functions and the ranking established by the test regarding the crossover operator.

Crossover		$\mathbf{f_{Ras}}$				$\mathbf{f_{Sch}}$				$\mathbf{f_{Ack}}$
I	J	$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$
CIXL2	BLX(0.3)	7.296e-01	0.923			2.715e+02	0.000			-2.830e-08	0.000
	BLX(0.5)	-9.950e-02	1.000			2.210e+02	0.010			-5.090e-08	0.000
	SBX(2)	-1.552e+01	0.000			-8.287e+02	0.000			-5.322e-06	0.000
	SBX(5)	-1.128e+01	0.000			-4.631e+02	0.000			-9.649e-06	0.000
	Fuzzy	-1.953e+01	0.000			-2.408e+03	0.000			-1.659e-07	0.000
	Logical	-6.033e+01	0.000			-1.988e+03	0.000			-2.517e-06	0.000
	UNDX	-1.078e+02	0.000			-7.409e+03	0.000			-3.550e-02	0.000
BLX(0.3)	CIXL2	-7.296e-01	0.923			-2.715e+02	0.000			2.830e-08	0.000
	BLX(0.5)	-8.291e-01	0.713			-5.050e+01	1.000			-2.261e-08	0.000
	SBX(2)	-1.625e+01	0.000			-1.100e+03	0.000			-5.293e-06	0.000
	SBX(5)	-1.201e+01	0.000			-7.346e+02	0.000			-9.620e-06	0.000
	Fuzzy	-2.026e+01	0.000			-2.680e+03	0.000			-1.376e-07	0.000
	Logical	-6.106e+01	0.000			-2.260e+03	0.000			-2.488e-06	0.000
	UNDX	-1.085e+02	0.000			-7.680e+03	0.000			-3.550e-02	0.000
BLX(0.5)	CIXL2	9.950e-02	1.000			-2.210e+02	0.010			5.090e-08	0.000
	BLX(0.3)	8.291e-01	0.713			5.050e+01	1.000			2.261e-08	0.000
	SBX(2)	-1.542e+01	0.000			-1.050e+03	0.000			-5.271e-06	0.000
	SBX(5)	-1.118e+01	0.000			-6.841e+02	0.000			-9.598e-06	0.000
	Fuzzy	-1.943e+01	0.000			-2.629e+03	0.000			-1.150e-07	0.000
	Logical	-6.023e+01	0.000			-2.209e+03	0.000			-2.466e-06	0.000
	UNDX	-1.077e+02	0.000			-7.630e+03	0.000			-3.550e-02	0.000
SBX(2)	CIXL2	1.552e+01	0.000			8.287e+02	0.000			5.322e-06	0.000
	BLX(0.3)	1.625e+01	0.000			1.100e+03	0.000			5.293e-06	0.000
	BLX(0.5)	1.542e+01	0.000			1.050e+03	0.000			5.271e-06	0.000
	SBX(5)	4.245e+00	0.005			3.655e+02	0.006			-4.327e-06	0.000
	Fuzzy	-4.013e+00	0.042			-1.579e+03	0.000			5.156e-06	0.000
	Logical	-4.481e+01	0.000			-1.159e+03	0.000			2.805e-06	0.000
	UNDX	-9.227e+01	0.000			-6.580e+03	0.000			-3.550e-02	0.000
SBX(5)	CIXL2	1.128e+01	0.000			4.631e+02	0.000			9.649e-06	0.000
	BLX(0.3)	1.201e+01	0.000			7.346e+02	0.000			9.620e-06	0.000
	BLX(0.5)	1.118e+01	0.000			6.841e+02	0.000			9.598e-06	0.000
	SBX(2)	-4.245e+00	0.005			-3.655e+02	0.006			4.327e-06	0.000
	Fuzzy	-8.258e+00	0.000			-1.945e+03	0.000			9.483e-06	0.000
	Logical	-4.905e+01	0.000			-1.525e+03	0.000			7.132e-06	0.000
	UNDX	-9.651e+01	0.000			-6.946e+03	0.000			-3.550e-02	0.000
Fuzzy	CIXL2	1.953e+01	0.000			2.408e+03	0.000			1.659e-07	0.000
	BLX(0.3)	2.026e+01	0.000			2.680e+03	0.000			1.376e-07	0.000
	BLX(0.5)	1.943e+01	0.000			2.629e+03	0.000			1.150e-07	0.000
	SBX(2)	4.013e+00	0.042			1.579e+03	0.000			-5.156e-06	0.000
	SBX(5)	8.258e+00	0.000			1.945e+03	0.000			-9.483e-06	0.000
	Logical	-4.079e+01	0.000			4.199e+02	0.000			-2.351e-06	0.000
	UNDX	-8.826e+01	0.000			-5.001e+03	0.000			-3.550e-02	0.000
Logical	CIXL2	6.033e+01	0.000			1.988e+03	0.000			2.517e-06	0.000
	BLX(0.3)	6.106e+01	0.000			2.260e+03	0.000			2.488e-06	0.000
	BLX(0.5)	6.023e+01	0.000			2.209e+03	0.000			2.466e-06	0.000
	SBX(2)	4.481e+01	0.000			1.159e+03	0.000			-2.805e-06	0.000
	SBX(5)	4.905e+01	0.000			1.525e+03	0.000			-7.132e-06	0.000
	Fuzzy	4.079e+01	0.000			-4.199e+02	0.000			2.351e-06	0.000
	UNDX	-4.746e+01	0.000			-5.421e+03	0.000			-3.550e-02	0.000
UNDX	CIXL2	1.078e+02	0.000			7.409e+03	0.000			3.550e-02	0.000
	BLX(0.3)	1.085e+02	0.000			7.680e+03	0.000			3.550e-02	0.000
	BLX(0.5)	1.077e+02	0.000			7.630e+03	0.000			3.550e-02	0.000
	SBX(2)	9.227e+01	0.000			6.580e+03	0.000			3.550e-02	0.000
	SBX(5)	9.651e+01	0.000			6.946e+03	0.000			3.550e-02	0.000
	Fuzzy	8.826e+01	0.000			5.001e+03	0.000			3.550e-02	0.000
	Logical	4.746e+01	0.000			5.421e+03	0.000			3.550e-02	0.000
Function	Ranking
$f_{Ras}$	$\mu_{UNDX} > \mu_{Logical} > \mu_{Ext.F.} > \mu_{SBX(2)} > \mu_{SBX(5)} > \mu_{BLX(0.5)} \ge \mu_{CIXL2} \ge \mu_{BLX(0.3)}$
$f_{Sch}$	$\mu_{UNDX} > \mu_{Ext.F.} > \mu_{Logical} > \mu_{SBX(2)} > \mu_{SBX(5)} > \mu_{CIXL2} > \mu_{BLX(0.5)} \ge \mu_{BLX(0.3)}$
$f_{Ack}$	$\mu_{UNDX} > \mu_{SBX(5)} > \mu_{SBX(2)} > \mu_{Logical} > \mu_{Ext.F.} > \mu_{BLX(0.5)} > \mu_{BLX(0.3)} > \mu_{CIXL2}$

Table 16: Results of the multiple comparison tests for $f_{Gri}$, $f_{Fle}$ and $f_{Lan}$ functions and the ranking established by the test regarding the crossover operator.

Crossover		$\mathbf{f_{Gri}}$				$\mathbf{f_{Fle}}$				$\mathbf{f_{Lan}}$
I	J	$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$			$\mathbf{\mu_I - \mu_J}$	$\mathbf{\alpha^*}$
CIXL2	BLX(0.3)	-3.224e-02	0.021			-4.779e+02	1.000			9.384e-02	0.091
	BLX(0.5)	-2.235e-02	0.012			-2.789e+03	1.000			1.392e-01	0.007
	SBX(2)	-6.710e-03	0.973			-1.740e+04	0.034			-1.253e-02	1.000
	SBX(5)	-1.603e-02	0.167			-1.810e+04	0.022			-1.982e-02	1.000
	Fuzzy	1.394e-02	0.000			-1.686e+03	1.000			-1.000e-01	0.000
	Logical	9.173e-03	0.057			-1.196e+04	0.709			-2.064e-01	0.000
	UNDX	-6.312e-02	0.000			-1.947e+04	0.009			6.557e-03	1.000
BLX(0.3)	CIXL2	3.224e-02	0.021			4.779e+02	1.000			-9.384e-02	0.091
	BLX(0.5)	9.893e-03	1.000			-2.311e+03	1.000			4.540e-02	1.000
	SBX(2)	2.553e-02	0.188			-1.693e+04	0.046			-1.064e-01	0.046
	SBX(5)	1.621e-02	0.952			-1.763e+04	0.029			-1.137e-01	0.013
	Fuzzy	4.618e-02	0.000			-1.208e+03	1.000			-1.938e-01	0.000
	Logical	4.142e-02	0.001			-1.148e+04	0.888			-3.003e-01	0.000
	UNDX	-3.088e-02	0.252			-1.899e+04	0.012			-8.728e-02	0.151
BLX(0.5)	CIXL2	2.235e-02	0.012			2.789e+03	1.000			-1.392e-01	0.007
	BLX(0.3)	-9.893e-03	1.000			2.311e+03	1.000			-4.540e-02	1.000
	SBX(2)	1.564e-02	0.361			-1.461e+04	0.179			-1.518e-01	0.004
	SBX(5)	6.320e-03	1.000			-1.531e+04	0.121			-1.591e-01	0.001
	Fuzzy	3.629e-02	0.000			1.104e+03	1.000			-2.392e-01	0.000
	Logical	3.152e-02	0.000			-9.169e+03	1.000			-3.457e-01	0.000
	UNDX	-4.077e-02	0.003			-1.668e+04	0.054			-1.327e-01	0.012
SBX(2)	CIXL2	6.710e-03	0.973			1.740e+04	0.034			1.253e-02	1.000
	BLX(0.3)	-2.553e-02	0.188			1.693e+04	0.046			1.064e-01	0.046
	BLX(0.5)	-1.564e-02	0.361			1.461e+04	0.179			1.518e-01	0.004
	SBX(5)	-9.320e-03	0.980			-7.002e+02	1.000			-7.285e-03	1.000
	Fuzzy	2.065e-02	0.000			1.572e+04	0.095			-8.747e-02	0.008
	Logical	1.588e-02	0.003			5.446e+03	1.000			-1.939e-01	0.000
	UNDX	-5.641e-02	0.000			-2.061e+03	1.000			1.909e-02	1.000
SBX(5)	CIXL2	1.603e-02	0.167			1.810e+04	0.022			1.982e-02	1.000
	BLX(0.3)	-1.621e-02	0.952			1.763e+04	0.029			1.137e-01	0.013
	BLX(0.5)	-6.320e-03	1.000			1.531e+04	0.121			1.591e-01	0.001
	SBX(2)	9.320e-03	0.980			7.002e+02	1.000			7.285e-03	1.000
	Fuzzy	2.997e-02	0.000			1.642e+04	0.063			-8.018e-02	0.004
	Logical	2.520e-02	0.001			6.146e+03	1.000			-1.866e-01	0.000
	UNDX	-4.709e-02	0.000			-1.361e+03	1.000			2.637e-02	1.000
Fuzzy	CIXL2	-1.394e-02	0.000			1.686e+03	1.000			1.000e-01	0.000
	BLX(0.3)	-4.618e-02	0.000			1.208e+03	1.000			1.938e-01	0.000
	BLX(0.5)	-3.629e-02	0.000			-1.104e+03	1.000			2.392e-01	0.000
	SBX(2)	-2.065e-02	0.000			-1.572e+04	0.095			8.747e-02	0.008
	SBX(5)	-2.997e-02	0.000			-1.642e+04	0.063			8.018e-02	0.004
	Logical	-4.763e-03	0.025			-1.027e+04	1.000			-1.064e-01	0.000
	UNDX	-7.706e-02	0.000			-1.778e+04	0.027			1.066e-01	0.000
Logical	CIXL2	-9.173e-03	0.057			1.196e+04	0.709			2.064e-01	0.000
	BLX(0.3)	-4.142e-02	0.001			1.148e+04	0.888			3.003e-01	0.000
	BLX(0.5)	-3.152e-02	0.000			9.169e+03	1.000			3.457e-01	0.000
	SBX(2)	-1.588e-02	0.003			-5.446e+03	1.000			1.939e-01	0.000
	SBX(5)	-2.520e-02	0.001			-6.146e+03	1.000			1.866e-01	0.000
	Fuzzy	4.763e-03	0.025			1.027e+04	1.000			1.064e-01	0.000
	UNDX	-7.229e-02	0.000			-7.507e+03	1.000			2.130e-01	0.000
UNDX	CIXL2	6.312e-02	0.000			1.947e+04	0.009			-6.557e-03	1.000
	BLX(0.3)	3.088e-02	0.252			1.899e+04	0.012			8.728e-02	0.151
	BLX(0.5)	4.077e-02	0.003			1.668e+04	0.054			1.327e-01	0.012
	SBX(2)	5.641e-02	0.000			2.061e+03	1.000			-1.909e-02	1.000
	SBX(5)	4.709e-02	0.000			1.361e+03	1.000			-2.637e-02	1.000
	Fuzzy	7.706e-02	0.000			1.778e+04	0.027			-1.066e-01	0.000
	Logical	7.229e-02	0.000			7.507e+03	1.000			-2.130e-01	0.000
Function	Ranking
$f_{Gri}$	$\mu_{UNDX} \ge \mu_{BLX(0.3)} \ge \mu_{BLX(0.5)} \ge \mu_{SBX(5)} \ge \mu_{SBX(2)} \ge \mu_{CIXL2} \ge \mu_{Logical} > \mu_{Ext.F.}$
$f_{Fle}$	$\mu_{UNDX} \ge \mu_{SBX(5)} \ge \mu_{SBX(2)} \ge \mu_{Logical} \ge \mu_{BLX(0.5)} \ge \mu_{Ext.F.} \ge \mu_{BLX(0.3)} \ge \mu_{CIXL2}$
$f_{Lan}$	$\mu_{Logical} > \mu_{Ext.F.} > \mu_{SBX(5)} \ge \mu_{SBX(2)} \ge \mu_{CIXL2} \ge \mu_{UNDX} \ge \mu_{BLX(0.3)} \ge \mu_{BLX(0.5)}$

Table 17: Results for all the functions of the multiple comparison test and the ranking obtained depending on the evolutionary algorithm.

$\mathbf{I}$

$\mathbf{J}$

$\mathbf{\mu_I - \mu_J}$

$\mathbf{\alpha^*}$

$\mathbf{\mu_I - \mu_J}$

$\mathbf{\alpha^*}$

$\mathbf{\mu_I - \mu_J}$

$\mathbf{\alpha^*}$

$\mathbf{\mu_I - \mu_J}$

$\mathbf{\alpha^*}$

$\mathbf{f_{SchDS}}$

$\mathbf{f_{Ros}}$

$\mathbf{f_{Ras}}$

$\mathbf{f_{Sch}}$

CIXL2

$UMDA_c$

-2.221e+01

0.000

-2.928e+00

0.000

-1.547e+02

0.000

-1.089e+04

0.000

$EGNA_{BGe}$

-2.076e-01

0.000

-2.906e+00

0.000

-1.533e+02

0.000

-1.091e+04

0.000

$UMDA_c$

CIXL2

2.221e+01

0.000

2.928e+00

0.000

1.547e+02

0.000

1.089e+04

0.000

$EGNA_{BGe}$

2.200e+01

0.000

2.207e-02

0.856

1.360e+00

0.888

-2.390e+01

0.677

$EGNA_{BGe}$

CIXL2

2.076e-01

0.000

2.906e+00

0.000

1.533e+02

0.000

1.091e+04

0.000

$UMDA_c$

-2.200e+01

0.000

-2.207e-02

0.856

-1.360e+00

0.888

2.390e+01

0.677

Function

Ranking

$f_{SchDS}$

$\mu_{UMDA_c} > \mu_{EGNA_{BGe}} > \mu_{CIXL2}$

$f_{Ros}$

$\mu_{UMDA_c}\ge\mu_{EGNA_{BGe}}>\mu_{CIXL2}$

$f_{Ras}$

$\mu_{UMDA_c}\ge\mu_{EGNA_{BGe}}>\mu_{CIXL2}$

$f_{Sch}$

$\mu_{EGNA_{BGe}}\ge\mu_{UMDA_c}>\mu_{CIXL2}$

$\mathbf{f_{Ack}}$

$\mathbf{f_{Gri}}$

$\mathbf{f_{Fle}}$

$\mathbf{f_{Lan}}$

CIXL2

$UMDA_c$

-1.101e-08

0.000

1.525e-02

0.000

9.803e+03

0.004

-3.306e-02

0.176

$EGNA_{BGe}$

-9.194e-09

0.000

1.525e-02

0.000

6.157e+03

0.150

-3.306e-02

0.176

$UMDA_c$

CIXL2

1.101e-08

0.000

-1.525e-02

0.000

-9.803e+03

0.004

3.306e-02

0.176

$EGNA_{BGe}$

1.817e-09

0.175

1.266e-16

0.000

-3.646e+03

0.049

1.33781e-11

0.325

$EGNA_{BGe}$

CIXL2

9.194e-09

0.000

-1.525e-02

0.000

-6.157e+03

0.150

3.306e-02

0.176

$UMDA_c$

-1.817e-09

0.175

-1.266e-16

0.000

3.646e+03

0.049

-1.33781e-11

0.325

Function

Ranking

$f_{Ack}$

$\mu_{UMDA_c}\ge\mu_{EGNA_{BGe}}>\mu_{CIXL2}$

$f_{Gri}$

$\mu_{CIXL2}>\mu_{UMDA_c}>\mu_{EGNA_{BGe}}$

$f_{Fle}$

$\mu_{CIXL2}\ge\mu_{EGNA_{BGe}}>\mu_{UMDA_c}$

$f_{Lan}$

$\mu_{UMDA_c}\ge\mu_{EGNA_{BGe}}\ge\mu_{CIXL2}$