Same-World Labelled Mutexes

There are several types of mutexes that can be added to the $LUG$ . To start with, we only concentrate on those that can evolve in a single possible world because same-world mutexes are more effective as well as relatively easy to understand. We extend the mutex propagation that was used in the multiple graphs so that the mutexes are on one planning graph. The savings of computing mutexes on the $LUG$ instead of multiple graphs is that we can reduce computation when a mutex exits in several worlds. In Appendix B we describe how to handle cross-world mutexes, despite their lack of effectiveness in the experiments we conducted. Cross-world mutexes extend the $LUG$ to compute the same set of mutexes found by CGP [30].

Same-world mutexes can be represented with a single label, $\hat{\ell}_k(x_1, x_2)$ , between two elements (actions, effect, or literals). The mutex holds between elements $x_1$ and $x_2$ in all worlds $S$ where $S \models \hat{\ell}_k(x_1, x_2)$ . If the elements are not mutex in any world, we can assume the label of a mutex between them is false $\perp$ . We discuss how the labelled mutexes are discovered and propagated for actions, effect relations, and literals.

By using mutexes, we can refine what it means for a formula $f$ to be reachable from a set of worlds $BS_P$ . We must ensure that for every state in $BS_P$ , there exists a state of $f$ that is reachable. A state $S'$ of $f$ is reachable from a state $S$ of $BS_P$ when there are no two literals in $S'$ that are mutex in world $S$ and $BS_P \models \ell_k^*(S)$ .

In each of the action, effect, and literal layers there are multiple ways for the same pair of elements to become mutex (e.g. interference or competing needs). Thus, the mutex label for a pair is the disjunction of all labelled mutexes found for the pair by some means.

Action Mutexes: The same-world action mutexes at a level $k$ are a set of labelled pairs of actions. Each pair is labelled with a formula that indicates the set of possible worlds where the actions are mutex. The possible reasons for mutex actions are interference and competing needs.

• Interference Two actions $a, a'$ interfere if (1) the unconditional effect consequent $\varepsilon^0(a)$ of one is inconsistent with the execution precondition $\rho^e(a')$ of the other, or (2) vice versa. They additionally interfere if (3) both unconditional effect consequents $\varepsilon^0(a)$ and $\varepsilon^0(a')$ are inconsistent, or (4) both execution preconditions $\rho^e(a)$ and $\rho^e(a')$ are inconsistent. The mutex will exist in all possible world projections $\hat{\ell}_k(a, a') = BS_P$ . Formally, $a$ and $a'$ interfere if one of the following holds:

  $$\begin{array}{l} {\tt (1)}\; \varepsilon^0(a) \wedge \rho^e(... ... {\tt (4)}\; \rho^e(a) \wedge \rho^e(a') = \perp \end{array}$$

  
  

• Competing Needs Two actions $a, a'$ have competing needs in a world when a pair of literals from their execution preconditions are mutex in the world. The worlds where $a$ and $a'$ are mutex because of competing needs are described by:

  $$\ell_k(a) \wedge \ell_k(a') \wedge \bigvee_{\substack{l \in \rho^j(a), l'\in \rho^j(a') }} \hat{\ell}_k(l, l')$$

  
  

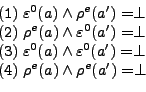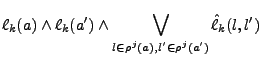  In the above formula we find all worlds where a pair of execution preconditions $l \in \rho^e(a), l'\in \rho^e(a')$ are mutex and both actions are reachable.

Effect Mutexes: The effect mutexes are a set of labelled pairs of effects. Each pair is labelled with a formula that indicates the set of possible worlds where the effects are mutex. The possible reasons for mutex effects are associated action mutexes, interference, competing needs, or induced effects.

• Mutex Actions Two effects $\varphi^i(a) \in \Phi(a), \varphi^{j}(a') \in \Phi({a'})$ are mutex in all worlds where their associated actions are mutex, $\hat{\ell}_k(a, a')$ .

• Interference Like actions, two effects $\varphi^i(a), \varphi^{j}(a')$ interfere if (1) the consequent $\varepsilon^i(a)$ of one is inconsistent with the antecedent $\rho^j(a')$ of the other, or (2) vice versa. They additionally interfere if (3) both effect consequents $\varepsilon^i(a)$ and $\varepsilon^j(a')$ are inconsistent, or (4) both antecedents $\rho^i(a)$ and $\rho^j(a')$ are inconsistent. The mutex will exist in all possible world projections, so the label of the mutex is $\hat{\ell}_k(\varphi^i(a), \varphi^{j}(a')) = BS_P$ . Formally, $\varphi^i(a)$ and $\varphi^{j}(a')$ interfere if one of the following holds:

  $$\begin{array}{l} {\tt (1)}\; \varepsilon^i(a) \wedge \rho^j(... ... {\tt (4)}\; \rho^i(a) \wedge \rho^j(a') = \perp \end{array}$$

  
  

• Competing Needs Like actions, two effects have competing needs in a world when a pair of literals from their antecedents are mutex in a world. The worlds where $\varphi^i(a)$ and $\varphi^{j}(a')$ have a competing needs mutex are:

  $$\ell_k(\varphi^i(a)) \wedge \ell_k(\varphi^{j}(a')) \wedge \bigvee_{\substack{l \in \rho^i(a), l'\in \rho^j(a') }} \hat{\ell}_k(l, l')$$

  
  

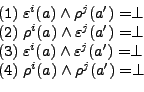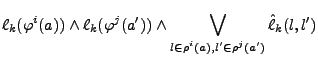  In the above formula we find all worlds where a pair of execution preconditions $l \in \rho^i(a), l'\in \rho^j(a')$ are mutex and both actions are reachable.

• Induced An induced effect $\varphi^j(a)$ of an effect $\varphi^i(a)$ is an effect of the same action $a$ that may execute at the same time. An effect is induced by another in the possible worlds where they are both reachable. For example, the conditional effect of an action always induces the unconditional effect of the action.

  Induced mutexes, involving the inducing effect $\varphi^i(a)$ , come about when an induced effect $\varphi^j(a)$ is mutex with another effect $\varphi^{h}(a')$ (see Figure 8). The induced mutex is between (a) the effect $\varphi^{h}(a')$ that is mutex with the induced effect $\varphi^j(a)$ and (b) the inducing effect $\varphi^i(a)$ . The label of the mutex is the conjunction of the label of the mutex $\hat{\ell_k}(\varphi^j(a), \varphi^{h}(a'))$ and the label of the induced effect $\varphi^j(a)$ . For additional discussion of the methodology behind induced mutexes we refer to [30].

  Figure 8: Effect $\varphi^i(a)$ induces effect $\varphi^j(a)$ . $\varphi^j(a)$ is mutex with $\varphi^{h}(a')$ , so $\varphi^i(a)$ is induced mutex with $\varphi^{h}(a')$ .

  

Literal Mutexes: The literal mutexes are a set of labelled pairs of literals. Each pair is labelled with a formula that indicates the set of possible worlds where the literals are mutex. The only reason for mutex literals is inconsistent support.

• Inconsistent Support Two literals have inconsistent support in a possible world at level $k$ when there are no two non-mutex effects that support both literals in the world. The label of the literal mutex at level $k$ is a disjunction of all worlds where they have inconsistent support. The worlds for an inconsistent support mutex between $l$ and $l'$ are:

  $$\bigvee_{\substack{S: \forall \varphi^i(a), \varphi^{j}(a') \in ... ...silon^{j}(a'),\ S \models \hat{\ell}_{k-1}(\varphi^i(a), \varphi^{j}(a'))}} S$$

  
  

  The meaning of the above formula is that the two literals are mutex in all worlds $S$ where all pairs of effects that support the literals in $S$ are mutex in $S$ .