|
|
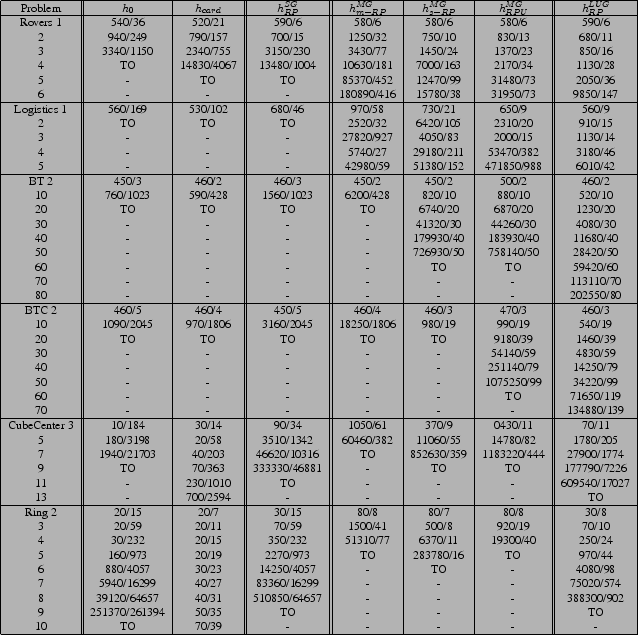
In the conformant domains, ![]() generally does better than
CAltAlt. This may be attributed in part to implementation-level
details.
generally does better than
CAltAlt. This may be attributed in part to implementation-level
details. ![]() makes use of an existing (highly optimized) BDD
package for belief state generation in progression, but as
previously mentioned, CAltAlt relies on a less optimized implementation
for belief state generation in regression. As we will see in the
next section, regression planners that employ a more sophisticated
implementation perform much better, but could still benefit from our
heuristics. Aside from a few differences that we will mention, we
see similar trends in the performance of the various heuristics in
both CAltAlt and
makes use of an existing (highly optimized) BDD
package for belief state generation in progression, but as
previously mentioned, CAltAlt relies on a less optimized implementation
for belief state generation in regression. As we will see in the
next section, regression planners that employ a more sophisticated
implementation perform much better, but could still benefit from our
heuristics. Aside from a few differences that we will mention, we
see similar trends in the performance of the various heuristics in
both CAltAlt and ![]() . Namely, the
. Namely, the ![]() and
and ![]() heuristics have
limited ability to help the planner scale, the
heuristics have
limited ability to help the planner scale, the ![]() heuristics help
the planner scale better but are costly, and the
heuristics help
the planner scale better but are costly, and the ![]() provides the
best scalability. The difference between the
provides the
best scalability. The difference between the ![]() and the
and the ![]() are
especially pronounced in Cube Center and Ring, where the size of the
initial belief state is quite large as the instances scale.
Interestingly in Ring, breadth first search and the single graph
relaxed plan are able to scale due to reduced heuristic computation
time and the low branching factor in search. The
are
especially pronounced in Cube Center and Ring, where the size of the
initial belief state is quite large as the instances scale.
Interestingly in Ring, breadth first search and the single graph
relaxed plan are able to scale due to reduced heuristic computation
time and the low branching factor in search. The ![]() is able to provide good
search guidance, but tends to take a long time computing heuristics in Ring.
is able to provide good
search guidance, but tends to take a long time computing heuristics in Ring.
We are also now able to compare the choices for aggregating the
distance measures from relaxed plans for multiple graphs. We see
that taking the maximum of the relaxed plans,
![]() , in
assuming positive interaction among worlds is useful in Logistics
and Rovers, but loses the independence of worlds in the BT and BTC
domains. However, taking the summation of the relaxed plan values
for different worlds,
, in
assuming positive interaction among worlds is useful in Logistics
and Rovers, but loses the independence of worlds in the BT and BTC
domains. However, taking the summation of the relaxed plan values
for different worlds,
![]() is able to capture the
independence in the BT domain. We notice that the summation does
not help
is able to capture the
independence in the BT domain. We notice that the summation does
not help ![]() in the BTC domain; this is because we overestimate
the heuristic value for some nodes by counting the Flush action once
for each world when it in fact only needs to be done once (i.e. we
miss positive interaction). Finally, using the
in the BTC domain; this is because we overestimate
the heuristic value for some nodes by counting the Flush action once
for each world when it in fact only needs to be done once (i.e. we
miss positive interaction). Finally, using the
![]() heuristic we do well in every domain, aside from the cost of
computing multiple graph heuristics, because we account for both
positive interaction and independence by taking the overlap of
relaxed plans. Again, with the
heuristic we do well in every domain, aside from the cost of
computing multiple graph heuristics, because we account for both
positive interaction and independence by taking the overlap of
relaxed plans. Again, with the ![]() relaxed plan, analogous to the
multiple graph unioned relaxed plan,
relaxed plan, analogous to the
multiple graph unioned relaxed plan, ![]() scales well because we
measure overlap and lower the cost of computing the heuristic
significantly.
scales well because we
measure overlap and lower the cost of computing the heuristic
significantly.
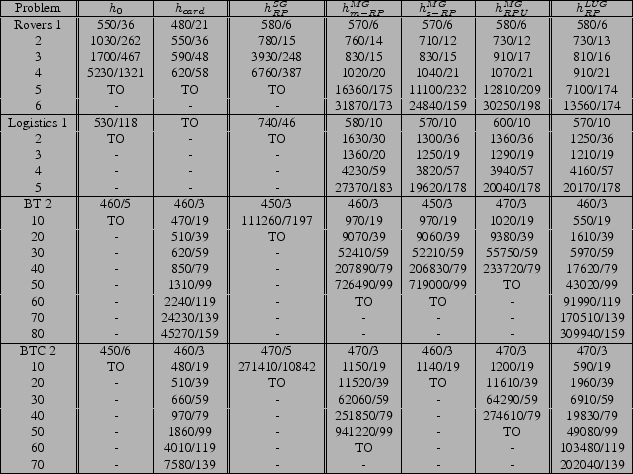
The main change we see in using ![]() versus CAltAlt is that the
direction of search is different, so the
versus CAltAlt is that the
direction of search is different, so the ![]() heuristic
performs unlike before. In the BT and BTC domains cardinality does
not work well in progression because the size of belief states does
not change as we get closer to the goal (it is impossible to ever
know which package contains the bomb). However, in regression we
start with a belief state containing all states consistent with the
goal and regressing actions limits our belief state to only those
states that can reach the goal through those actions. Thus in
regression the size of belief states decreases, but in progression
remains constant.
heuristic
performs unlike before. In the BT and BTC domains cardinality does
not work well in progression because the size of belief states does
not change as we get closer to the goal (it is impossible to ever
know which package contains the bomb). However, in regression we
start with a belief state containing all states consistent with the
goal and regressing actions limits our belief state to only those
states that can reach the goal through those actions. Thus in
regression the size of belief states decreases, but in progression
remains constant.
The performance of ![]() in the conditional domains exhibits
similar trends to the conformant domains, with a few exceptions.
Like the conformant domains, the
in the conditional domains exhibits
similar trends to the conformant domains, with a few exceptions.
Like the conformant domains, the ![]() relaxed plans tend to
outperform the
relaxed plans tend to
outperform the ![]() relaxed plan, but the
relaxed plan, but the ![]() relaxed plan does
best overall. Unlike the conformant domains, The
relaxed plan does
best overall. Unlike the conformant domains, The
![]() performs much better in BTS and BTCS over BT and BTC partly because
the conditional plans have a lower average cost. The
performs much better in BTS and BTCS over BT and BTC partly because
the conditional plans have a lower average cost. The ![]() heuristic does better in BTS and BTCS over BT and BTC because the
belief states actually decrease in size when they are partitioned by
sensory actions.
heuristic does better in BTS and BTCS over BT and BTC because the
belief states actually decrease in size when they are partitioned by
sensory actions.