Next: PDDL+ and Hybrid Automata Up: Formalism Previous: Planetary Lander Example
We now consider whether PDDL+ represents a real extension to the expressive power of PDDL2.1. Of course, the fragment of PDDL2.1 that was used in the competition and has been widely used since (the fragment restricted to discrete durative actions) does not include the parts that express continuous change, and without those elements PDDL2.1 is certainly less expressive than PDDL+. In this section we discuss the differences between modelling continuous change using the continuous durative action constructs of PDDL2.1, and modelling it using the start-process-stop model.
PDDL2.1, complete with continuous durative actions, comprises a powerful modelling language. Allowing continuous effects within flexible duration actions offers an expressive combination that appears close to the processes and events of PDDL+. The essential difference between the languages arises from the separation, in PDDL+, between the changes to the world that are directly enacted by the executive and those indirect changes that are due to physical processes and their consequences.
To model physical processes and their consequences in PDDL2.1 requires the addition to the domain model of artificial actions to simulate the way in which processes and events interact with eachother and with the direct actions of the executive. For example, to force intervals to abut, so that the triggering of an event is correctly modelled, requires artificial actions that force the corresponding end points of the intervals to synchronise. These actions must be applied by the planner, since there is no other dynamic to force indirect events to coincide in the way that they would coincide in nature. In earlier work [Fox LongFox Long2004] we show how clips can be constructed in PDDL2.1 and used to achieve this effect. Clips prevent time passing between the end points of actions modelling the background behaviour of the world. The example shown in Figure 7 illustrates how clips can be used to model interacting continuous effects in a PDDL2.1 representation of the Planetary Lander Domain.
![\includegraphics[height=3in]{chargedischarge}](img23.png) |
The example shows two activities executing against a backdrop of continuous charging and discharging of a battery. The bell-shaped curve represents the solar power production, which starts at daybreak, reaches its peak at midday and then drops off to zero at nightfall. Two concurrent power-consuming activities, A and B, are executing during the daylight hours. The stepped curve shows their (cumulative) power requirements. A PDDL+ representation of this plan would contain just the two actions A and B -- the processes and events governing power consumption and production would be triggered autonomously and would not be explicit in the plan. By contrast, a PDDL2.1 representation of the same plan would contain durative actions for each of the episodes of charge, C, and discharge, D, which need to be precisely positioned (using clips) with respect to the two activities A and B. Clips are required because actions C and D do not have fixed durations so they have to be joined together to force them to respect the underlying timeline. The two dotted rectangles of the figure depict a PDDL2.1 plan containing 28 action instances in addition to A and B. Of these, there are four points simulating the intersections between the supply and the demand curves that do not correspond to the end points of actions A and B. A planner using a PDDL2.1 model is forced to construct these points in its simulation of the background behaviours. All of the necessary clip actions would be explicit in the plan.
As can be seen, the construction of an accurate simulation in PDDL2.1 is far from trivial. Indeed, although this is not an issue that we highlight in the example, there are cases where no simulation can be constructed to be consistent with the use of ![]() -separation for interfering action effects. This occurs when events or process interactions occur with arbitrarily small temporal separations. Even where simulations can be constructed, the lack of distinction between direct and indirect causes of change means that a planner is forced to construct the simulated process and event sequences as though they are part of the plan it is constructing. This means that the planner is required to consider the simulation components as though they are choice points in the plan construction, leading to a combinatorial blow up in the cost of constructing plans.
-separation for interfering action effects. This occurs when events or process interactions occur with arbitrarily small temporal separations. Even where simulations can be constructed, the lack of distinction between direct and indirect causes of change means that a planner is forced to construct the simulated process and event sequences as though they are part of the plan it is constructing. This means that the planner is required to consider the simulation components as though they are choice points in the plan construction, leading to a combinatorial blow up in the cost of constructing plans.
The explicit distinction between actions and events yields a compact plan representation in PDDL+. A PDDL2.1 plan, using a simulation of the events and processes, would contain explicit representations of every happening in the execution trace of the PDDL+ plan. The fact that the PDDL2.1 plan represents a form of constructive proof of the existence of an execution trace of the PDDL+ plan is one way to understand Theorem 1 below: the work in validating a PDDL+ plan is that required to construct the proof that a PDDL2.1 plan would have to supply explicitly.
By distinguishing between the direct action of the executive and the continuous behaviours of the physical world we facilitate a decomposition of the planning problem into its discrete and continuous components. This decomposition admits the use of hybrid reasoning techniques, including Mixed Integer Non-Linear Programming (MINLP) [GrossmannGrossmann2002], Benders Decomposition [BendersBenders1962], Branch-and-Bound approaches that relax the discrete components of the domain into continuous representations [AndroulakisAndroulakis2001], and other such techniques that have proved promising in mixed discrete-continuous problem-solving [Wu ChowWu Chow1995]. By contrast, trying to treat a hybrid problem using purely discrete reasoning techniques seems likely to result in an unmanageable combinatorial explosion. Of course, the trade-offs cannot be fully understood until planners exist for tackling mixed discrete-continuous domains featuring complex non-linear change.
We now prove that PDDL+ has a formally greater expressive power than PDDL2.1.
To simulate an arbitrary RM program, we need an action that will initiate execution of the program:
(:action start
:parameters ()
:precondition ()
:effect (started))
Now we construct a family of events that simulate execution of the program. We use an encoding of a register machine with three instructions: inc(j,k) which increments register ![]() and then jumps to instruction
and then jumps to instruction ![]() , dec(j,k,z), which tests register
, dec(j,k,z), which tests register ![]() and jumps to instruction
and jumps to instruction ![]() if it is zero and otherwise decrements it and jumps to instruction
if it is zero and otherwise decrements it and jumps to instruction ![]() , and HALT which terminates the program. We assume that the instructions are labelled
, and HALT which terminates the program. We assume that the instructions are labelled
![]() and the registers used are labelled
and the registers used are labelled
![]() . We also assume that instruction 0 is the start of the program.
. We also assume that instruction 0 is the start of the program.
(:event beginExection
:parameters ()
:precondition (started)
:effect (and (not (started))
(in_0)))
For an instruction of the form: ![]() : inc(j,k) where
: inc(j,k) where ![]() is the label, we construct:
is the label, we construct:
(:event doFor an instruction of the form: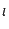
:parameters ()
:precondition (in_)
:effect (and (not (in_))
(in_)
(increase (reg_) 1)))
(:event doFinally, for an instruction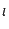
:parameters ()
:precondition (in_)
:effect (and (not (in_))
(when (= (reg_) 0) (in_
))
(when (> (reg_) 0) (and (decrease (reg_
) 1)
(in_)))))
(:event doWe now create an initial state in which registers reg_0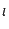
:parameters ()
:precondition (in_)
:effect (and (not (in_))
(halted)))
1: (beginExecution)
is valid if and only if the computation of the embedded RM halts. Therefore, a general plan validation system for PDDL+ would have to be able to solve the halting problem.
Theorem 1 is a formal demonstration of the increase in expressive power offered by PDDL+. It depends on the fact that a PDDL+ plan is defined to exclude explicit indication of events and processes that are triggered during the execution of the plan. It might be argued that this is an artificial problem, but there are two points to consider. Firstly, by avoiding the requirement that events and processes be captured explicitly in the plan we remain agnostic about the nature of the reasoning that a planner might perform about these phenomena. It might be that a planner can synthesise an approximation of a continuous process that simplifies the reasoning and is sufficiently accurate to allow it to place its actions around the process behaviour, but that would be insufficient to determine the precise moments at which the process triggers events. Secondly, a planner might be able to determine that some collection of processes and events is irrelevant to the valid execution of a plan it has constructed to solve a problem, even though it is apparent that some pattern of processes and events will be triggered during the execution of the plan. In this case, the requirement that the plan correctly and explicitly captures all of this background activity is an unreasonable additional demand.
The undecidability of the PDDL+ validation problem need not be confronted in practice. If certain restrictions are imposed (no cascading events, functions restricted to polynomials and some exponentials), which do not undermine the ability to capture realistic domains, the processes and events underlying a PDDL+ plan can be efficiently simulated using well-known numerical methods. In [Fox, Howey, LongFox et al.2006] we show how numerical simulation is achieved in the PDDL+ plan validator, VAL. A validation procedure must simulate these processes and events to ensure that critical values remain in acceptable ranges throughout the plan (and satisfy the conditions of planned actions). The restrictions that it is sensible to apply, in particular to sequences of events that may be triggered at the same time point, but also to the forms of continuous functions that arise in a domain, do not prevent us from achieving close approximations of realistic behaviours. Boddy and Johnson boddy and Hofmann and Williams brian use linear and quadratic approximations to model complex non-linear functions. We use a quartic approximation and an inverse exponential function to represent the power dynamics in our own model of the planetary lander (see Appendix C).
In practice, although there is a formal separation between the expressive power of PDDL+ and PDDL2.1, the conceptual separation between the activities of the executive and those of the world is the most important feature of PDDL+.
We now present a simple family of domains to illustrate that PDDL2.2 encodings grow larger than PDDL+ domains encoding equivalent behaviours. The difference arises from the fact that durative actions encapsulate not only the way in which a process starts, but also the way it concludes. This means that in domains where there is a significant choice of different ways to start and end a process, the PDDL2.1 encoding expands faster than the corresponding PDDL+ encoding. Consider the PDDL+ domain containing the following action and process schemas:
(:action A
:parameters ()
:precondition (and (not (started)) (a))
:effect (and (started) (not (a)) (assign (dur)
))
)
(:action B
:parameters ()
:precondition (and (b) (= (C) (* (dur)
))
:effect (and (not (started)) (done))
)
(:process P
:parameters ()
:precondition (started)
:effect (increase (C) (* #t 1))
)
The action schemas are families A![]() and B
and B![]() , indexed by
, indexed by ![]() and
and ![]() which take values
which take values
![]() and
and
![]() respectively. The values
respectively. The values ![]() and
and ![]() are (different) action-instance-dependent constants. Any plan starting in an initial state
are (different) action-instance-dependent constants. Any plan starting in an initial state
![]() , with
, with ![]() , that achieves done, must contain the actions
, that achieves done, must contain the actions ![]() , separated by exactly
, separated by exactly ![]() . To encode an equivalent durative action model requires an action schema:
. To encode an equivalent durative action model requires an action schema:
(:durative-action AB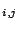
:parameters ()
:duration (= ?duration (*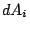
))
:condition (and (at start (a)) (at end (b
)))
:effect (and (at start (not (a))) (at end (done)))
)
As can be seen, the size of the encoding of the family of PDDL+ domains grows as ![]() , while the corresponding size of the PDDL2.2 encodings grows as
, while the corresponding size of the PDDL2.2 encodings grows as ![]() . The need to couple each possible initiation of the process with each possible conclusion to the process leads to this multiplicative growth. Reification of the propositions in the durative action encoding can be used to reduce the encoding to an
. The need to couple each possible initiation of the process with each possible conclusion to the process leads to this multiplicative growth. Reification of the propositions in the durative action encoding can be used to reduce the encoding to an ![]() encoding, but the ground action set continues to grow as
encoding, but the ground action set continues to grow as ![]() compared with the
compared with the ![]() growth of the ground actions and processes for the PDDL+ model.
growth of the ground actions and processes for the PDDL+ model.
It is clear that it is easier to build the plan given the ![]() encoding, because this provides ready-made solutions to the problem. However, the trade-off to be explored lies in how large a representation can be tolerated to obtain this advantage in general. It is always possible to compile parts of the solution to a problem into the problem representation, but the price that is paid is in the size of the encoding and the effort required to construct it. On this basis we argue that a compact representation is preferable. The example we have presented is an artificial example demonstrating a theoretical difference in the expressive powers of PDDL2.2 and PDDL+. It remains to be seen whether this phenomenon arises in practice in realistic domains.
encoding, because this provides ready-made solutions to the problem. However, the trade-off to be explored lies in how large a representation can be tolerated to obtain this advantage in general. It is always possible to compile parts of the solution to a problem into the problem representation, but the price that is paid is in the size of the encoding and the effort required to construct it. On this basis we argue that a compact representation is preferable. The example we have presented is an artificial example demonstrating a theoretical difference in the expressive powers of PDDL2.2 and PDDL+. It remains to be seen whether this phenomenon arises in practice in realistic domains.