Durative Actions in PDDL+

The syntax for durative actions can be seen as a purely syntactic convenience. In order to support this view, durative actions must be mapped directly into an equivalent start-process-stop representation using the basic syntax of PDDL+. The reason for performing the mapping is in order to give durative actions a semantics in terms of the underlying structures of PDDL+, which are themselves given meaning in terms of hybrid automata as discussed in Section 6. The mapping is as follows.

Consider the following generic structure for a PDDL2.1 durative action, excluding the use of duration inequalities and continuous effects. Conditional effects are ignored, since they can be handled by flattening the actions as described in Core Definition 5. The complication of conditional effects that combine initial and final conditions is discussed in [Fox LongFox Long2003] and does not affect the basic principles we demonstrate in the translation we give here. Similarly, for convenience, we do not consider duration constraints referring to the end state -- extension of the treatment below to manage these constraints is straightforward.

(:durative-action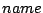 $name$

:parameters ($\vec{p}$)

:duration (= ?duration 
$Dur[\vec{p}]$)

:condition (and (at start $Pre_{S}$) (at end $Pre_{E}$) (over all $Inv$))

:effect (and (at start $Post_{S}$)(at end $Post_{E}[$?duration$]$))

)

We now construct the following structures in PDDL+:

(:action $name$-start

:parameters ($\vec{p}$)

:precondition (and $Pre_{S}$ (not ($name$_clock_started $\vec{p}$)))

:effect (and $Post_{S}$

($name$_clock_started $\vec{p}$)

(assign ($name$_clock $\vec{p}$) 0)

(assign ($name$_duration $\vec{p}$) 
$Dur[\vec{p}]$)

(increase (clock_count) 1))



(:process $name$-process

:parameters ($\vec{p}$)

:precondition ($name$_clock_started $\vec{p}$)

:effect (increase ($name$_clock $\vec{p}$) (* #t 1))



(:event $name$-failure

:parameters ($\vec{p}$)

:precondition (and ($name$_clock_started $\vec{p}$)

(not (= ($name$_clock $\vec{p}$) ($name$_duration $\vec{p}$)))

(not $Inv$))

:effect (assign ($name$_clock $\vec{p}$) (+ ($name$_duration $\vec{p}$) 1)))



(:action $name$-end

:parameters ($\vec{p}$)

:precondition (and $Pre_{E}$ ($name$_clock_started $\vec{p}$)

(= ($name$_clock $\vec{p}$) ($name$_duration $\vec{p}$)))

:effect (and $Post_{E}[$($name$_duration $\vec{p}$)$]$

(not ($name$_clock_started $\vec{p}$))

(decrease (clock_count) 1)))

To complete the transformation, the initial state has the (= (clock_count) 0) added to it and the goal has the condition (= (clock_count) 0) added to it.

Note that the clock is uniquely determined by the name and arguments of the durative action, so the clock is not shared between different durative actions. Also note that there is only one action that can start each such clock and only one that can terminate it. If a plan makes use of the durative action then in the transformed domain the durative action can be simulated by the actions that start and stop the clock. In order for these actions to execute successfully the conditions must be identical to those stipulated in the durative action and their effects are equivalent to the original durative action. Furthermore, the end action can only be executed once the clock has reached the correct duration value (which is recorded at the start). The clock is driven by a process that is active only once the start action has been executed and only until the end action is executed. An event is used to monitor the invariant conditions. If ever the invariant becomes false while the clock is running then the event sets the clock to be after the duration of the durative action. This makes it impossible to complete the action and terminate the clock, so that no valid execution trace can be constructed to achieve the goal in which the event is triggered. Every time a clock starts a count is incremented and it is decremented when a clock stops. The count must be zero at the end, meaning that every clock must have stopped and therefore every durative action must have been ended before the plan is complete.

The duration of the action is managed by using a metric fluent to store the duration at the outset in order to use the value at the conclusion of the action. If the value is a fixed constant then this can be simplified by replacing the metric fluent with the appropriate constant.

Packaging actions, events and processes into a durative action abstracts the details of how the interval ends -- whether by an action or by an event. For example, if a durative action is used to represent the activity of filling a bath, its end point will represent the action of turning off the taps, whilst in a durative action representing a ball being dropped, the end of the action is the event of the ball landing. However, there is no syntactic difference between the structures encoding these examples that allows a distinction to be drawn between an end point that is an action and one that is an event. The mapping of durative actions into actions, processes and events requires an arbitrary decision to be made about how to handle the end points of durative actions. While we have chosen to use actions, an alternative formulation is possible using events.

The mapping converts every durative action into the family of PDDL+ constructs shown above -- two actions to start and end the interval, a process to execute during the interval,and a monitoring event for the invariant. Because an action is always used to end the interval a planner must always choose to apply it in order to obtain a goal state. In the final plan the terminating action will appear, chosen by the planner, even though its application is in fact forced, and its point of application must be consistent with the duration constraint of the original durative action. Thus, although the planner is free to choose whether and when to apply the action, in order to construct a valid plan it is forced to apply the action at a point that exactly meets the appropriate temporal constraints. Of course, the end points of the simulated durative actions can be trivially post-processed to make a plan containing durative actions instead of to their underlying components.