7.3 Communication Overhead

Here we show that, depending on bandwidth, latency, and how summary information is communicated among the agents, delays due to communication overhead vary. If only communication costs are a concern, then at one extreme where message delay dominates cost, sending the plan hierarchy without summary information makes the most sense. At the other extreme where bandwidth costs dominate, it makes sense to send the summary information for each task in a separate message as each is requested. Still, there are cases when sending the summary information for tasks in groups makes the most sense. This section will explain how a system designer can choose how much summary information to send at a time in order to reduce communication overhead exponentially.

Consider a simple protocol where agents request coordination from a central coordinating agent. During the search for a feasible solution, whenever it decomposes a task, the coordinator requests summary information for the subtasks that it has not yet received. For the manufacturing domain, the coordinator may already have summary information for a task to move a part, but if it encounters a different instantiation of the same task schema, it still must request the parameters for the new task. If a coordinator needs the subplans of an $or$ plan, the client agent sends the required information for all subplans, specifying its preferences for each. The coordinator then chooses the most preferred subplan, and in the case it must backtrack, it chooses the next most preferred subplan. Once the coordinator finds a feasible solution, it sends modifications to each agent specifying which $or$ subplans are blocked and where the agent must send and wait for synchronization messages. An agent can choose to send summary information for some number of levels of expansion of the requested task's hierarchy.

For the manufacturing problem described in Section 1.1, communication data in terms of numbers of messages and the size of each was collected up to the point that the coordinator found the solution in Figure 13c. This data was collected for cases where agents sent summary information for tasks in their hierarchies, one at a time, two levels at a time, and all at once. The two levels include the requested task and its immediate subplans. The following table below summarizes the numbers and total sizes of messages sent for each granularity level of information:

Figure 32: Delay of communicating different granularities of summary information with varying a) latency and b) bandwidth

Assuming that the coordinator must wait for requested information before continuing its search and can request only one task of one agent at a time, the coordination will be delayed for an amount of time depending on the bandwidth and latency of message passing. The total delay can be calculated as $(n-2)\ell + s/b$, where $n$ is the number of messages sent; $\ell$ is the latency in seconds; $s$ is the total size of all messages; and $b$ is the bandwidth in bytes per second. We use $n-2$ instead of $n$ because we assume that the agents all transmit their first top-level summary information message at the same time, so three messages actually only incur a delay of $\ell$ instead of $3\ell$.

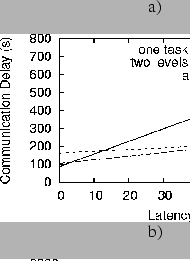
Figure 32a shows how the communication delay varies for the three granularities of information for a fixed bandwidth of 100 bytes/second. (We will address the lack of realism in this example shortly.) When the latency is less than 3 seconds, sending summary information for each task in separate messages results in the smallest communication overhead. For latencies greater than 58 seconds, sending the entire hierarchy is best; and in between sending summary information two levels at a time is best. If the latency is fixed at 100 seconds, then the communication delay varies with bandwidth as shown in Figure 32b. When the bandwidth is less than 3 bytes/second, sending one at a time is best; sending it all at once is best for bandwidths greater than 60 bytes/second; and sending two levels at a time is best for bandwidths in between.

Admittedly, these values are unrealistic for the manufacturing domain. The manufacturing problem itself is very simple and provided mainly as an interesting domain for coordination. More realistic problems involving the manufacturing domain could have much larger hierarchies and require much larger scales of data to be sent. In that case more realistic bandwidth and latency values would exhibit similar tradeoffs.

To see this, suppose that the manufacturing managers' hierarchies had a common branching factor $b$ and depth $d$. If tasks generally had reservations on similar resources throughout the hierarchies, the amount of total summary information at a particular level would grow exponentially down the hierarchy just as would the number of tasks. If the agents agreed on a feasible solution at depth level $i$ in the hierarchy, then the table for messages and size would appear as follows:

Now suppose that the branching factor $b$ is 3; the depth $d$ is 10; the solution is found at level $i=5$; and the summary information for any task is 1 Kbyte. Then the table would look like this:

Figure 33: Delay with varying a) latency and b) bandwidth for hypothetical example

Now, if we fixed the bandwidth at 100 Kbyte/second and varied the latency, more realistic tradeoffs are seen in Figure 33a. Here, we see that unless the latency is very small, sending summary information two levels at a time is best. As shown in Figure 33b, if we fix latency to be one second and vary the bandwidth, for all realistic bandwidths sending summary information two levels at a time is again best.

This simple protocol illustrates how communication can be minimized by sending summary information at a particular granularity. If the agents chose not to send summary information but the unsummarized hierarchies instead, they would need to send their entire hierarchies. As the experiment shows, as hierarchies grow large, sending the entire hierarchy (``all at once'') would take a long time, even with a high bandwidth. Thus, using summary information (as opposed to not using it) can reduce communication exponentially when solutions can be found at abstract levels.

At the other extreme, if the agents sent summary information one task at a time, the latency for sending so many messages can grow large for larger task hierarchies. If solutions could only be found at primitive levels, then sending summary information one task at a time would cause an exponential latency overhead compared to sending the entire hierarchy at once. But, if solutions can be found at intermediate levels, being able to send summary information at some intermediate granularity can minimize total delay.

However, this argument assumes that summary information collapses at higher levels in the hierarchy. Otherwise, sending summary information at some intermediate level could be almost as expensive as sending the entire hierarchy and cause unnecessary overhead. For the actual manufacturing domain, tasks in the agents' hierarchies mostly have constraints on different resources, and summarization is not able to reduce summary information significantly because constraints do not collapse. The result is that it is better, in this case, to send the entire hierarchy at once to minimize delay (unless there are unusual bandwidth and latency constraints, as shown in the experiment). Even so, the coordination agent can still summarize the hierarchies itself to take advantage of the computational advantages of abstract reasoning.

This section showed how a domain modeler can minimize communication overhead by communicating summary information at the proper level of granularity. If bandwidth, latency, and a common depth for coordination solutions is known, the domain modeler can perform a hypothetical experiment like the one above for varying granularities of summary information to determine which granularity is optimal. If summary information collapses up the hierarchy, and solutions can be found at intermediate levels, then communication can be exponentially reduced in this manner.