Results

Table 1 lists 30 theorems that cause SPIKE to diverge and the lemmas speculated by the divergence critic after analysing the diverging proof attempts. These problems provide a representative sample of the type of theorems for which the cause of divergence can be identified and an appropriate lemma or generalization speculated. Many of these problems come from the CLAM library corpus. Part of this table has appeared before [19]. Times are for the divergence critic to speculate the lemmas and are for the average of 10 runs on a Sun 4 running QUINTUS 3.1.1.

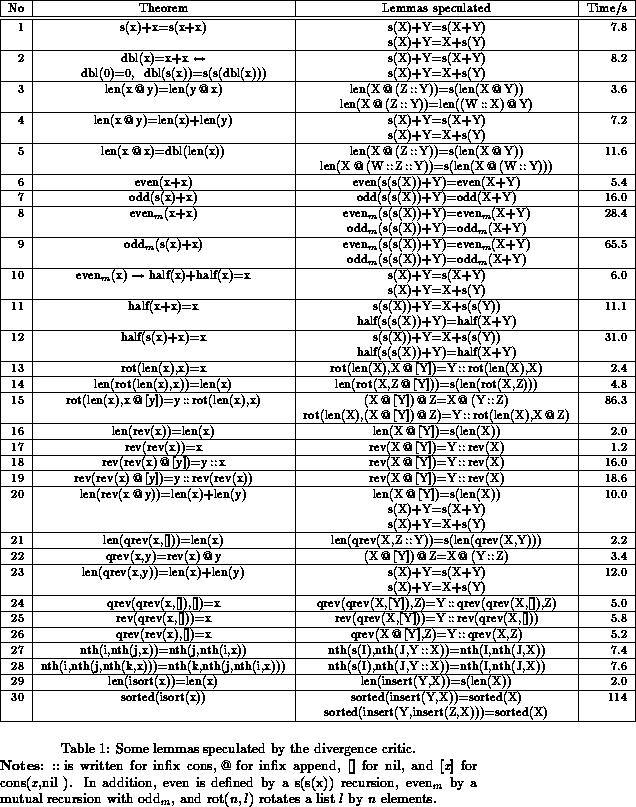
SPIKE's proof attempt diverges on each example when given the definitions alone. In each of the 30 cases, the critic is quickly able to suggest a lemma which overcomes divergence. When multiple lemmas are proposed (with the exception of 20) any one on its own is sufficient to fix divergence. In every case (except 13 and 24) the lemmas proposed are sufficiently simple to be proved automatically without introducing fresh divergence. In the majority of cases, the lemmas proposed are optimal; that is, they are the simplest possible lemmas which fix divergence. In the cases when the lemma is not optimal, they are usually only slightly more complex than the simplest lemma which fixes divergence. In many of the examples, other lemmas are conjectured by the divergence analysis but these are quickly rejected by the conjecture disprover. For example, in example 16, divergence analysis and the petering out heuristic suggest the rule,

However, this is refuted by exhaustive normalization using any ground terms for and . In this case, the cancellation heuristic identifies the required lemma,

Some of the examples deserve additional comment. In example 1, the divergence critic identifies that successor functions are accumulating on the first argument position of +. The critic speculates a lemma for moving these successor functions either to the top of the term (so that immediate cancellation can occur) or onto to the second argument position (so that simplification with the recursive definition of + can occur). The first lemma speculated is in fact a generalization of the theorem being proved. Example 2 is a simple program verification problem taken from Dershowitz and Pinchover (1990). The forward direction of this theorem was discussed in the introduction. Similar divergence occurs as in example 1 and, after generalization, the same lemmas are speculated.

Example 3 caused divergence in the beta-version of SPIKE available in the summer of 1994. The proof rules in SPIKE have since been strengthened and this example no longer causes divergence in the current release. The speculated lemmas do, however, simplify the proof. Example 4 was used in the text to illustrate the generalization heuristics. The second lemma in example 5 is perhaps a little surprising, Although it is more complex than the first lemma, it is nearly as good at fixing divergence.

In example 6, the lemma proposed, is not optimal. That is, it is not the simplest possible lemma that fixes divergence. To fix divergence, we merely need one of the rules, or . Either of these will ripple the successor functions accumulating on the first argument position of +. The divergence critic attempts to construct a lemma to ripple two successor functions across from the first to the second argument positions of +. Unfortunately, the critic fails to find an appropriate instantiation for the right hand side of such a lemma. The critic instead proposes a rule to move the two successor functions up to the top of the term where the wave-front can peter out. Example 7 is very similar to example 6.

Examples 8 to 10 demonstrate that the critic can cope with divergence in theories involving mutual recursion. In example 8, SPIKE attempts to prove by induction the equations,

The critic identifies two inter-linking divergence patterns,

The critic therefore proposes rules which ripple this accumulating term structure up to the top of the term where it peters out,

Just as in examples 6 and 7, these are not the optimal rules for fixing divergence. Nevertheless, either of the proposed rules fix divergence and both can be proved without difficulty by SPIKE. Example 9 is very similar to example 8.

Examples 10 to 12 require little comment. In example 13, the proposed lemma is too difficult to be proved automatically. However, the divergence critic is able to identify the cause of this difficulty and propose a lemma which allows the proof to go through (example 15). In example 14, the speculated lemma is not optimal. The simpler lemma speculated in example 13 would be adequate to prove this theorem without divergence. The speculated lemma is not optimal because the divergence critic attempts to ripple the accumulating term structure over two functors, and to the top of the term tree. However, it is sufficient on this problem to ripple it up over just one functor, .

Examples 16 to 19 are straightforward and do not require discussion. In example 20, the critic identifies two separate divergence patterns. To overcome divergence, the first lemma plus one or other of the second and third are therefore needed. The first divergence pattern occurs in the sequence of subgoals,

Term structure is accumulating on the second argument of append. Such term structure is removed by the first rule,

The second divergence pattern occurs in the sequence of subgoals,

Term structure is accumulating on the first argument of +. This is removed by one or other of the second and third rules,

Examples 21 and 23 are reasonably straightforward. The lemma speculated in example 22 is a special case of the associativity of append. More powerful generalization heuristics could have speculated the associativity of append. However, such heuristics would also speculate more non-theorems. Further research into the optimal strength of generalization heuristics would be valuable.

Example 24 is the only disappointment; the lemma proposed fixes divergence but is too difficult to be proved automatically, even with the assistance of the divergence critic. See example 34 at the end of this section for more details. Example 25 is discussed in more detail in the related work in Section 9 as it demonstrates the superiority of difference matching over generalization techniques for divergence analysis. Examples 26 to 28 require little discussion. Finally, examples 29 and 30 demonstrate that the critic can cope with divergence in moderately complex theories containing conditional equations.

The results are very pleasing. Using the divergence critic, the 30 theorems listed (with the exception of 24) can all be proved from the definitions alone. To provide an indication of the difficulty of these theorems, the NQTHM system [8], which is perhaps the best known explicit induction theorem prover, was unable to prove more than half these theorems from the definitions alone. To be precise, NQTHM failed on 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 18, 19, 21, 22, 24, 25, 26, 27 and 28. Of course, with the addition of some simple lemmas, NQTHM is able to prove all these theorems. Indeed, in many cases, NQTHM needs the same lemmas as those proposed by the divergence critic and required by SPIKE. This suggests that the divergence critic is not especially tied to the particular prover used nor even to the implicit induction setting.

To test this hypothesis, I presented the output of a diverging proof attempt from NQTHM to the critic. I chose the commutativity of multiplication as this is perhaps the simplest theorem which causes NQTHM to diverge. The critic proposed the lemma,

         (EQUAL (TIMES Y (ADD1 X)) (PLUS Y (TIMES Y X))))

The divergence critic has several limitations. Recognizing divergence is, in general, undecidable since it reduces to the halting problem. The divergence critic will therefore sometimes fail to identify a diverging proof attempt. In addition, the critic will sometimes identify a ``divergence'' pattern when the proof attempt is not diverging. Even when divergence is correctly identified, the critic will sometimes fail to speculate an appropriate lemma. Finally, the critic only speculates wave-rules. Whilst many theories contain a large number of wave-rules, and these are often very useful for fixing divergence, other types of lemma can be needed.

Table 2 lists four theorems on which the divergence critic fails. These problems are representative of the different ways in which the critic can fail. The two main cause of failure are overlapping divergence patterns, and the inability of the heuristics to speculate an appropriate right hand side for a lemma. Again times are those to speculate lemmas and not to find a proof of the theorem.

Example 31 is a commuted version of the recursive definition of multiplication ( is defined recursively on its second argument position). SPIKE's attempt to prove this theorem diverges, generating the following sequence of equations,

Divergence analysis of the left hand sides of these equations suggests the need for a rule of the form,

Unfortunately the heuristics for lemma speculation are not sufficiently strong to suggest a suitable instantiation for (for example, ). This lemma is rather complex and is the result of two overlapping divergence patterns. If the annotations are considered separately, they suggest the rules,

With these two rules, SPIKE finds a proof without difficulty.

Example 32 is the commutativity of multiplication. The divergence critic identifies a divergence pattern and proposes the transverse wave rule,

However, SPIKE is unable to prove the commutativity of multiplication with the addition of this rule. The proof attempt is now somewhat simpler and contains the diverging sequence of equations,

Unfortunately the heuristics for instantiating the right hand side of speculated lemmas are not strong enough to suggest the rule,

With this rule, SPIKE finds a proof of the commutativity of multiplication without difficulty. The difficulties in speculating this rule arise because the wave-front is stuck in a similar position on both sides of the equality. There are few clues therefore to suggest how to ripple it up to the top of the term tree.

In example 33, the divergence critic proposes a lemma where one is not needed. SPIKE is able to find a proof of this theorem from the definitions alone using 16 inductions. Three of these inductions are on the equations,

This sequence of equations satisfies the divergence critic's preconditions. The critic therefore proposes wave rules for moving accumulating successor functions off the first argument position of +. Although the proposed lemmas are not necessary, either give a much shorter and simpler proof needing just 7 inductions.

Example 34 is the lemma speculated in example 24. Divergence analysis of SPIKE's attempt to prove this theorem identifies term structure accumulating on the second (alias accumulator) argument of . The first two lemmas proposed for removing this term structure are of no use as they are subsumed by the recursive definition of . The third lemma also fails to prevent divergence. This lemma simplifies two element lists in the second argument position of . However, divergence will still occur as the prover cannot simplify lists that occur in the second argument position of which contain 3 or more elements. Divergence can be overcome if we introduce a derived function for appending onto the end of a list. This can be used to simplify terms in which a list of arbitrary size occurs on the second argument position of . For example, we can simplify with the rule, Unfortunately, append does not occur in the specification of the theorem so it is difficult to find a heuristic that would speculate such a rule.