[Next] [Up] [Previous]

The Clustering Algorithm

We provide a sketch of the clustering algorithm in this section. Readers interested in more details are referred to [Shachter, Andersen, SzolovitsShachter et al.1994, Jensen, Lauritzen, OlesenJensen et al.1990, Shenoy ShaferShenoy \ Shafer1986].

According to the clustering method, we start by:

1. constructing a join tree of the given belief network;[+]
2. assigning the matrix of each variable in the belief network to some cluster that contains the variable's family.

The join tree is a secondary structure on which the inference algorithm operates. We need the following notation to state this algorithm:

-

are the clusters, where each cluster corresponds to a set of variables in the original belief network.

-

is the potential function over cluster , which is a mapping from instantiations of variables in into real numbers.

-

is the posterior probability distribution over cluster , which is a mapping from instantiations of variables in into real numbers.

-

is the message sent from cluster to cluster , which is a mapping from instantiations of variables in into real numbers.

-

is the given evidence, that is, an instantiation of evidence variables .

We also assume the standard multiplication and marginalization operations on potentials.

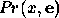Our goal now is to compute the potential which maps each instantiation of variable in the belief network into the probability . Given this notation, we can state the algorithm as follows:

• Potential functions are initialized using
  
  where
  • is a variable whose matrix is assigned to cluster ;
  • is the matrix for variable : a mapping from instantiations of the family of into conditional probabilities; and
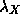  • is the likelihood vector for variable : is 1 if is consistent with given evidence and 0 otherwise.
• Posterior distributions are computed using
  
  where are the clusters adjacent to cluster .
• Messages are computed using
  
  where are the clusters adjacent to cluster .
• The potential is computed using
  
  where is a cluster to which belongs.

These equations are used as follows. To compute the probability of a variable, we must compute the posterior distribution of a cluster containing the variable. To compute the posterior distribution of a cluster, we collect messages from neighboring clusters. A message from cluster to is computed by collecting messages from all clusters adjacent to except for .

This statement of the join tree algorithm is appropriate for situations where the evidence is not changing frequently since it involves computing initial potentials each time the evidence changes. This is not necessary in general and one can provide more optimized versions of the algorithm. This issue, however, is irrelevant in the context of generating Q-DAGs because updating probabilities in face of evidence changes will take place at the Q-DAG level, which includes its own optimization technique that we discuss later.

[Next] [Up] [Previous]