Apply-to-each

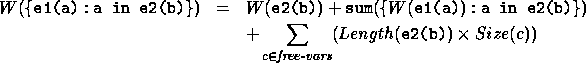
Equations 1 and 2 specified how the work and depth complexities could be combined in an apply-to-each. In the current implementation there are a couple caveats. The first concerns work complexity. In the following discussion we will consider a variable constant with regards to an apply-to-each if the variable is free (not bound) in the body of the apply-to-each and is not defined in bindings of the apply-to-each. For example, in

 {foo(a,b*c): b in s}  

the variables a and c are free with regards to the apply-to-each, while b is not. We will refer to these variables as free-vars. In the current implementation all free-vars need to be copied across the instances of an apply-to-each. This copying requires time, and the equation for combining work complexity that includes this cost is:

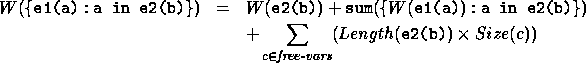
where the last term has been added to Equation 1 ( refers to the length of the sequence returned by e2(b), and refers to the size of each free-var). If a free-var is large, this copy could be the dominant cost of an apply-to-each. Here are some examples of such cases:

In both cases the work is a factor of #a greater than we might expect since the sequence a needs to be copied over the instances. As well as requiring extra work these copies require significant extra memory and can be a memory bottleneck in a program. Both the above examples can easily be rewritten to reduce the work and memory:

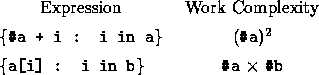
The user should be conscious of these costs and rewrite such expressions.

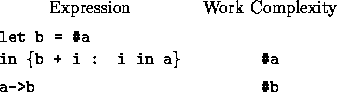
A second problem with the current implementation is that Equation 2

(the combining rule for the depth) only holds if the body of the apply-to-each is contained. The definition of contained code is code where only one branch of a conditional has a non-constant depth. For example, the following function is not contained because both branches of the inner if have :

This can be fixed by calculating power(a, n/2) outside the conditional:

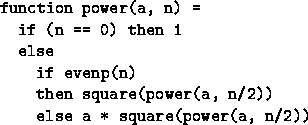
function power(a, n) =
  if (n == 0) then 1
  else
    let pow = power(a, n/2) 
    in if evenp(n)
       then square(pow)
       else a * square(pow)

In future implementations of NESL it is likely that this restriction will be removed.

{