
INTERNAL fMRI experiments page
Principal component analysis

This file is /afs/cs/project/theo-35/fmri/www/pca.html.
This page is for internal use by members of this project.
It can also be accessed from "http://www.cs.cmu.edu/afs/cs/project/theo-35/fmri/www/" inside the ".cmu.edu" domain.

Inspired from:
McKeown MJ, T-P. Jung, Makeig S, Brown GG, Kindermann SS, Sejnowski TJ, Spatially Independent Activity Patterns in Functional Magnetic Resonance Imaging Data During the Stroop Color-naming Task. Proceedings of the National Academy of Sciences USA, 95, pp.803-810, February 1998. (PostScript file)
Assumptions:
- The activity of the voxels of interest can be modeled as the
superposition of a small number of independent signals.
- Each of these signals originates from a particular region of the
brain.
- Some of the signals are correlated to the taks performed by the
subject.
Approach:
- Perform principal component analysis for the set of voxels.
- Project the activity of all voxels to the first few principal
directions, producing principal waveforms.
- Associate the principal directions with the source of the principal
waves.
- Correlate the principal waves with the task being performed.
- If successful, suggest that the location of processing for the
task coincides with the principal location of the correlated signal.
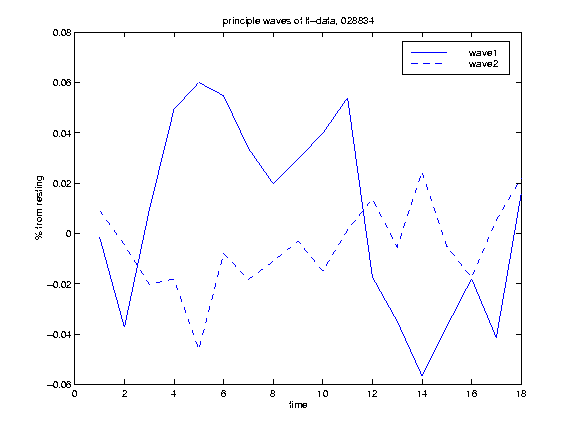
Results for 028834:
Left Broca:
First and second principal components (waves):

First principal direction ("eigenlocation"):
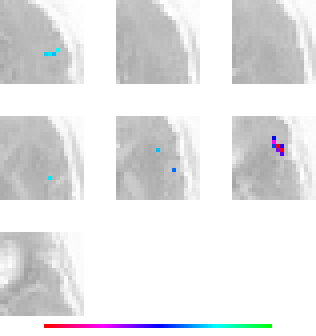
Second principal direction ("eigenlocation"):
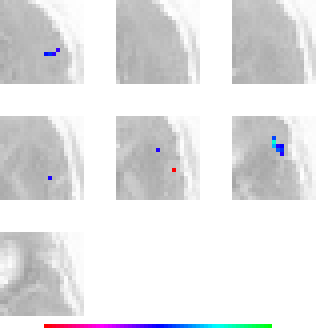
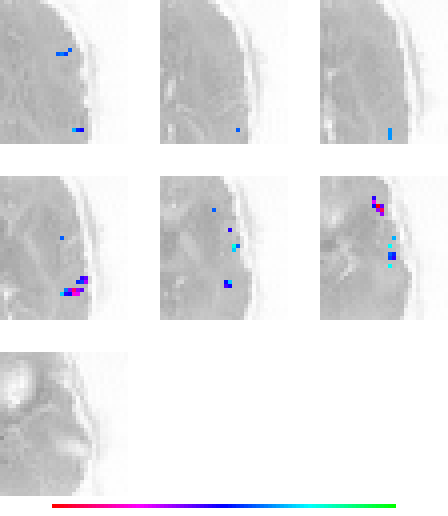
Left Wernicke:
First and second principal components (waves):
First principal direction ("eigenlocation"):
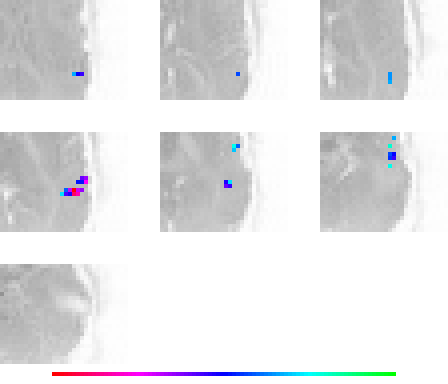
Second principal direction ("eigenlocation"):
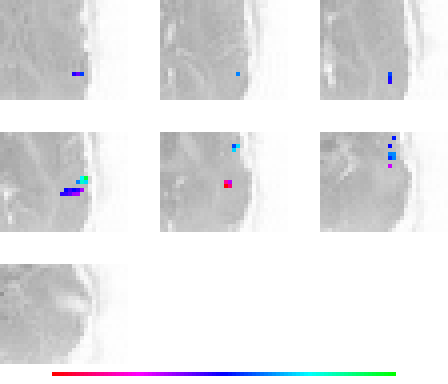
Left Broca and Wernicke:
First and second principal components (waves):

First principal direction ("eigenlocation"):
Second principal direction ("eigenlocation"):

Last updated Tue Mar 16 10:13:10 EST 1999 by Daniel












