
Thanks to Bill Spight for pointing out where I had a backup copy of this file!
In trying to understand the SST ko rule, I collected the strange positions shown below.
Other bestiaries are from
There arise two related issues:

Game termination gets confused with the issue of how many passes terminate the game and what the players can do after passing. Various situations that promise irremovable ko threats or infinite places to play need to be considered.
Where various rule sets differ on the interpretation of kos, I distinguish
between NK (Nihon Kiin, Japanese-style), AGA (Chinese-style), and SST
(Ing-style) rules. The possibilities are
ko fight - a ko threat is required by each player on each iteration
standoff - both groups remain on the board ("seki")
void game - the game must be replayed
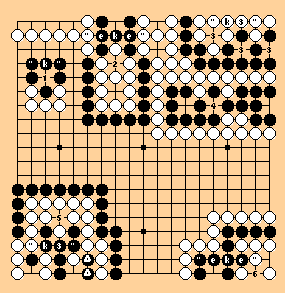
1. "k"- Simple ko. [All: ko fight]
2. "eke" - Two one-eyed groups sharing a ko. [All: ko fight]
3. "k3" - Triple ko. [NK: void game; SST, AGA: ko fight]
4. "k" - Simple ko, but potential loss is much bigger for black. [All:
ko fight]
5. "k3" - Triple ko with ko strings of length two. [NK: void game; SST,
AGA: ko fight]
6. "eke" - Two one-eyed groups sharing a ko. [All: ko fight]
Eternal Life


5@1, 6@2, 7@3, 8@4, and so on, but ko threats may be required.
A pseudo triple ko. If it is White's move, the black stones will die.


1. "k4" - Quadruple ko. [NK: void game; SST, AGA: standoff]
2. "ekke" - Each group has an eye and a ko space. [All: standoff]
3. "ek3" - Triple ko, but one group has an eye. [NK: void game; SST:
standoff; AGA: ko fight]
4. "ek4e" - The black group has two ko spaces and it divides two white
groups which each have one eye and one ko space. [NK: void game; SST,
AGA: standoff]
5. "ksk" - Each group has a ko and a shared liberty. [All: standoff]
6. "rar" - ("Ring-around-a-rosie.") Each of four groups has an eye and
a ko space. [NK: void game; SST: standoff; AGA: ko fight]
k5 - Quintuple ko. [NK: void game; SST, AGA: standoff]
Some commentators on the SST rules have claimed that the two sides
of a standoff both have the same number of liberties. K5 shows that
they do not.

k4(2) - Quadruple ko with double hot stones. [NK: void game; SST,
AGA: standoff]

"k3d" - Triple ko with a dame.
Both groups have two liberties in two places, and a capture by black and another by white converts this to another balanced configuration, so maybe this is a standoff. The answer depends on whether "external" liberties count towards balance. It would be nice if they did, because it is not easy to define the difference between the two types of liberties.
Neither player will fill the outside liberty: if black did so, the black group would die and if white filled, black would capture a ko and force white to make the first ko threat. The situation could be allowed to remain on the board as a seki.
Jasiek@berlin.snafu.edu (28-Jun-96) "k3d" *is* FK under SST: According to GoWorld 71, "A Comparison of the New Ko Rules" life and death are determined by identifying breaths types. First analyse breaths types: 3 internal ko breaths, 1 external dame. Only internal breaths are relevant for determining life and death. The relevant breaths are not balanced. Thus it is a FK. Due to the external liberty it is a 1-step approach-move ko for W.
Three related situations exploring the notion of "balance." Kim,Simon,Straus define balance as
[KSS 6.B]Balanced kos are distinguished in that each side must have the same number (at least two each) of separate internal liberties.
This definition is inadequate.
"Balanced? 1"
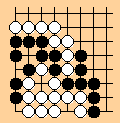
My original comment:
balanced, will be a standoff
equal liberties (3) in two or more disjoint regions (per KSS)
Jasiek@berlin.snafu.edu (28-Jun-96):
For balance by virtue of ko breaths at least two ko breaths, which can be paired, are necessary. Here B has a 2-step approach-move ko. W may create a seki, if he likes to; it will then be balanced.
Jasiek is correct. The definition in Kim,Simon,Straus is flawed because it omits the need for paired ko breaths.
"Balanced? 2"

The liberties are not KSS-balanced, B has three and W 2. If it is
Black's turn, a black stone at point a will produce a standoff. If
it is White's turn, the players can fight a ko at b for the life of
the black stones. Thus Black, starting with more liberties, could
lose. (Of course one of those liberties is a useless false eye.)
"Balanced? 3"
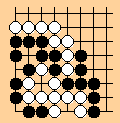
Black has 3 liberties to white's 2
Not yet balanced, but will be (unless Black chooses to defend the ko
fight as in the previous diagram).
Back-to-back sending-two-returning-one.
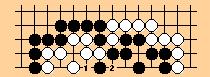
Both inner groups are alive, but if black plays at 1, white must respond
at 2. And then white would have a ko threat to the right of 2. Use
of these threats as part of a ko fight will be prohibited in my version
of the SST rules because they will become part of the cycle set. Even
without a form of super-ko, this situation is unlikely to be infinite
since the player who is ahead in score will refuse to continue the
iteration.
External liberties
Some attempts at describing the SST ko rules invoke the notion of external
liberties, which is hard to define. For instance, in what cases
is the liberty at a an external liberty for the black string in this
diagram?
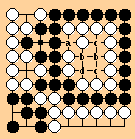
Jasiek attacks the notion of external liberties by showing a pair which
together constitute an internal liberty. In this diagram,

under SST rules, the inner black group is alive in a double ko standoff, using the two kos at c and d. The white group on the right has an eye and the two kos. The inner black group looks like it has two kos and two external liberties at a and b. However, those two external liberties each constitute half an eye; when White saves one of the two jeopardized stones, Black will capture the other to make an internal liberty.

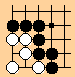

White may try to claim that the upper left group cannot be captured because when black plays at 1, white makes a ko threat in the lower right. Black also uses the lower right for a ko threat, a cycle is established, and the four ko positions in the lower right are entered into the restricted set for the ko at 1. Thereafter white must make ko threats elsewhere, but black need never make threats. If pushed to demonstrate capture, black plays on until white has no ko threats; black captures at 1 and white has no ko threats so white passes and black captures the group.

"ekkee"- pseudo-standoff. The three inner groups all have two internal
liberties in two disjoint segments. And yet this is not a standoff
because there is no other balanced configuration. In fact, the white
group in the corner is dead because white will have to make ko threats,
but black can always retreat to capturing the other ko in the local
situation.
TKO = Two-Kos-One-liberty
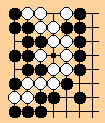
pre-TKO
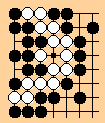
TKO

TKO

Non-stand-off double ko - Dead but a fount of ko threats
From Kim, Simon, and Straus
Not a standoff. White's upper right group and black's upper group
both have two liberties in two places, but there is no other balanced
configuration of these groups.
Sending two and returning one

Black plays at 1, white captures, and black recaptures at x. The board position has recurred with the opposite player to play. This is not a problem for the rules; no cycle or double hemicycle will occur because white will play elsewhere. (Note that black has blundered and must make a gote move to re-establish the seki.)

ridgway@inls1.ucsd.edu (Doug Ridgway)
28 Nov 1995 03:38:36 GMT
rec.games.go
Equivalent to sending two and returning one.
Triple ko stones (SST)



The initial ko is at 1-8. When black recaptures the ko with 11, a cycle is established and all the points played are in the restricted set for the ko at 1-8. White cannot play 12 at 2. Probably white's best move would be to play 2 at 3, but then white loses the game anyway.
Mega-cycle (John Bate)

If either player fills the upper ko, all the opponent's stones will be captured. Clearly this is a ko worth fighting. If a cycle starts with the upper ko and goes twice through all three kos, the stones in the lower kos will be part of the restricted set for the upper ko and cannot thereafter be used for ko threats. Black and white will have to find large threats elsewhere. They could each use the lower situation as a ko threat, but only once.
Black and white can both initiate hemicyles in the bottom two kos and both groups have two liberties, so this part of the board is itself a stand-off until white's external liberty is filled, at which time the lower white group would become a TKO.
Two TKOs
In their explanation of the SST ko rule, Kim/Simon/Straus describe a situation which is one of the primary reasons for development of the SST rule.

Under the Ing ko rule, each side is allowed to initiate a cyclic sequence, even one that involves the whole board, once but only once. Since the whole board position may repeat, White is allowed to capture at C but Black will then be prohibited from capturing at A, starting a second cycle.
To avoid capture, the false-eyed player will need to begin the ko cycle, but will then be prohibited from initiating the cycle a second time, and so will die.
The rules given in section 2 above, recognize black as a TKO in each corner and forbid capture in either except as a ko threat. So black could not initiate the cycle more than once.
Non-stand-off double ko - Dead but a fount of ko threats
From Kim, Simon, and Straus:

The analysis by the rules above is a little different: Just as in example 7, the upper edge is not a stand-off because black would be foolish to use it as a ko threat or initiate a hemicycle since the white stones are already dead.
Suppose, however, that there is an identical situation in another corner of the board, but with the colors reversed. Now each player has an infinite source of ko threats, so a cycle could arise as part of a fight over another ko elsewhere. By the definitions, the stones at 4, a, 1, and b in the two identical situations will all be in the restricted set for the local situation of that other ko. Thus they cannot be further played as ko threats.
Six kos, no repeated cycle. (Dave Ring)
At one time there was a belief that Ing's ko rule prevented two successive occurrences of the same cycle and that this prevented an infinite game record. Dave Ring posted the following counter: an artficial game in which no cycle of moves is ever repeated back-to-back.
Here is the position with B to move:

Assume we have an infinite sequence of {1, 2, 3} as described in the rec.puzzles archive, Scientific American and elsewhere. Call that sequence S. [The sequence never repeats any substring back to back.]
Replace the second, fourth, sixth etc occurrences of 1 by 1'. Similarly replace the even occurrences of 2 by 2' and 3 by 3'.
For example: 1 2 3 2 1 3 1 2 2 1... becomes 1 2 3 2' 1' 3' 1 2 2' 1' ...
Now replace:
1 -> Bd1 Wq1 [change bottom kos]
1' -> Br1 Wc1 [restore bottom kos]
2 -> Ba10 Wt10 [change middle kos]
2' -> Bt11 Wa11 [restore middle kos]
3 -> Bd19 Wq19 [change top kos]
3' -> Br19 Wc19 [restore top kos]
The result is a game record which never repeats a sequence of moves of any length.
The proof is by contradiction.
Assume there is a sequence XY where X and Y are identical sub-sequences
of length n. n is even because both sub-sequences must start with
the same color to move.
Case 2: If they start with W to move, then consider X' and Y' . X'
starts with the B move just before the first move of X . And Y' starts
with the B move just before the first move of Y . (X' Y' X and Y all
have length n.) The first move of X' is the same as the first move
of Y' because the moves are uniquely paired. The rest of the moves
of X' are the same as the rest of the moves of Y'. Thus X' = Y' and
we have Case 1 .
The objection raised by this example does not apply to the rules stated above because restricted sets are established as soon as a cycle restarts. Since there are but a finite number of kos in the example, eventually the board position will return to a position encountered earlier and the player to move will capture in the same ko as the last time the position occurred. Then all the kos that were touched during that cycle become part of the restricted set and cannot be captured in response to the player's latest move. Since black moves first in each pair of captures, black will make that final ko capture and white will be unable to save the white portion of the situation. White plays elsewhere, black captures a white group, and now white could initiate the same sort of shenanigans until capturing a black group. Each player wins two of the ko battles.
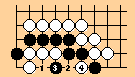
Molasses ko
The intrigue of the Molasses Ko is evidenced by the fact that both the British and American Go Journals published articles on it. The British came first. I am grateful to Harry Fearnley for sending me a copy of the article.
The position shown in the diagram came up in a game at CLGC [Central London Go Club ?]. The position is rather interesting in itself, and it might be amusing to ask if anyone can define the status.
White has just taken the ko, and it is assumed that the ko threats are not big enough to affect what is going on.
In the actual game, Black got fed up with it and let white capture
the whole group.
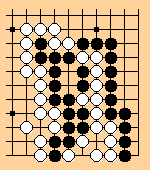
o In BGJ 94 (page 29) T. Mark Hall invited definitions of the status of a group....
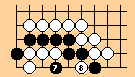
Status: if neither player is prepared to allow these stones to be captured, the game is a draw [using Japanese rules]. The play goes as follows:
1. Black: tenuki or pass. Black cannot retake the ko, and if he plays to secure the false eye he puts himself into atari.
2. White: atari. Either of the points in Black's eye will do. White cannot defend the ko as this would put him in atari.
3. Black: Capture the stone on the edge to retake the ko and place white in atari. Black cannot capture White 2 as White would then capture all the stones in a snapback.
4. White: capture. He must capture two stones as he is in atari and cannot retake the ko to gain an extra liberty.
5. Black: must capture the white stone on line 2 as he is now in atari. The positions are now reversed. Black has two liberties on lines 1 and 2, and White has two liberties on lines 6 and 7. The same sequence can now be played out in reverse...
6. White: tenuki or pass. As in the case of Black 1, he can neither retake the ko nor secure a single eye.
7. Black: atari on line 6 or 7.
8. White: capture the stone on line 2.
9. Black: capture the stones on lines 6 and 7.
10. White: capture the stone on line 1. The position is now exactly as before with up to two extra stones on the rest of the board.
If neither player will allow his stones to be captured, the game will have to be a draw. If either player is winning by more than about 30 points, they can allow these stones to be captured and still win, so the strategy is to win the game by allowing the stones to be captured. If neither player is winning by more than 30 points, neither can afford to be captured and hence the result must be a draw.
This assumes that neither player can force their opponent to reply to the tenuki. If that happens after a certain number of cycles, the play is then:
1. Black: tenuki. Forces a repy.
2. White: tenuki in reply to Black 1.
3. Black captures stone on line 1.
4. White: tenuki. The atari on line 6 or 7 is pointless because...
5. Black: captures all the White stones.
A position similar to the above was sent to me (wjh) by Andre Engels <csg419@wing.rug.nl> in mail dated Fri, 28 Oct 1994. Unaware of its earlier publication in the British Go Journal, I published Engels's analysis in the American Go Journal under the title "Molasses Ko" where I concluded:
I don't believe any ko rules apply because there are no cycles and the groups never both have the same number of liberties. The game simply proceeds sloooowly, like strolling through molasses.
But the real fun begins if this position arises in a game played under a superko rule (no repetition of the whole board after any number of plays). Because in this case it is fatal to use your free move as a pass, and you suddenly find that the game has reverted to the primitive form of go in which passing constitutes a loss. The concept of territory is still there, but it can be worth quite a few points to play loose stones inside your opponent's territory. This is sometimes referred to as 'Conway Go' after J. H. Conway's work on games in which the loser is the first player unable to find a legal move.
It looks to me like this position distinguishes superko from SST ko.
Consider the original position as it must have been prior to White's
first capture specified in the problem statement. And suppose there
are NO plays elsewhere on the board.
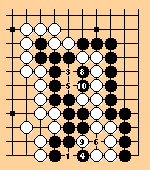
W1, B2 pass, W3, B4, W5, B6, W7 pass, B8, W9, B10 repeats the original position. Under the superko rule, Black cannot play B10 and loses the Black group. Under wjh-SST rules, B10 is allowed since it does not repeat an earlier capture and W11 at 1 is allowed since it is the capture which initiated the cycle. But now the rule simply says that Black cannot play B12 at any of the points 1...10; but there are none of them that Black wants to play at anyway! The next capture that repeats a cycle B4 and then W5 is prohibited. Thus White loses the white group!
With the official SST rules, I am not sure which move would be forbidden to break the cycle. Perhaps 3 would be considered a game disturbing move and would be disallowed. This is unfair because White has to make all the ko threats.
If passing is prohibited, one player will be the first to run out of outside places to play; that player will be unable to tenuki at the appropriate point in the cycle and will lose. That same player is fated to lose anyway since the other player has more places to play and therefore more points (except that there is a penalty of two points for the eyes of each group, so a player with fewer groups has the advantage.)
Suppose the position is this

If it is Black's move, he could get a standoff with a play at A, or
start the molasses ko with B. (C would let White choose between standoff
and ko.) Under superko, Black will start the ko only if he has sufficiently
large threats elsewhere. Under wjh-SST rules Black will start the
ko both is he has sufficiently large threats and if there are no places
left to play on the board.
If it is White's move, A and B are both losing strategies, so white
plays at C.

Black at A is a simple loss, so Black starts the molasses ko at B or
captures at D. Black needs a big ko threat to start the molasses
ko. If Black captures at D, White gets to choose between a standoff
and starting a molasses ko that may be hard for White to win.
An ambiguity in the SST rules may give difficulty with the molasses ko at the end of a game. Let us suppose there are NO places to play on the remainder of the board, so playing on the board ouside the molasses ko is not possible; each player must pass once during a cycle of the molasses ko. The rule on passing states:
Note that there is no specified procedure for resolving disputes about whether a group is dead or alive. One player may make a second consecutive pass believing his opponent's stones are dead in the molasses ko. Which player plays the first stone when play resumes? Since there is NO place to play, there are no dead stones to take away. In what order are the final two passes made? After the first final pass, can the opponent resume play in the molasses ko?
Finally, how is a game with a molasses ko forced to terminate? Neither
fighting ko nor disturbing ko seems a sufficient rule to force the
players to stop playing.
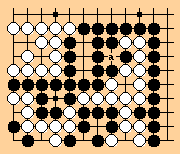
In the SST rules, as in AGA and New Zealand, black can fill at a without
penalty. So scoring is not an issue. The bottom is not a standoff,
because after a hemicycle the groups differ in number of liberties.
The situation is, however, interesting to analyze if we imagine that
white insists that black demonstrate that the lower left white group
is dead. Play might proceed thusly


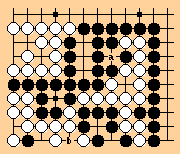
If white starts by taking at a, black may be in even more trouble.

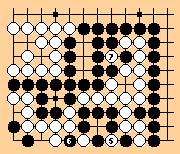
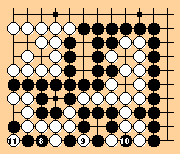

From: jasiek@berlin.snafu.de (Robert Jasiek)
To: wjh@cmu.edu
Subject: Tossed salad under Nihon Kiin rules
Date: Sat, 29 Jun 1996 12:53:14 GMT
So the game shall end with all 3 kos being taken once each and the ko at a still not connected. Black can treat all 4 kos - including the bent-4 ko - one after another seperately, since neither white is interested in filling a ko nor can white retake any ko without a particular pass play for each.
Thus in the theoretical line of play black finally takes all white stones off the board. All white stones are dead and removed for counting. So even if black does not connect at a before the end of the game, black wins by 0.5.

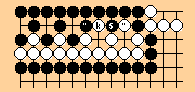
Two black strings and a white string each have two liberties and are
thus all peers. If white captures at point a, the white string gets
three liberties and the black strings both get one. The capture at
a is a linking capture and the three strings are all part of a linked
set. When black captures at b, all three strings become peers again,
so the capture by white at point a is thereafter disallowed.
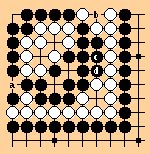
The top left black string and the bottom right white string are peers with two liberties each. Disallowed moves are moot, however, since black can connect a ko and live, killing white. Whichever ko white captures, black can capture the other and again have the option of connecting a ko to live.
The disallowance of captures does affect whether the game terminates.
As the corner stands, white can capture once at a and once at b, but
thereafter cannot play here. However, if c and d are empty, there
are no peer groups and no disallowed captures will occur. Black can
cause the game to terminate by filling c and d when white kmakes gote
moves elsewhere (at the end of the game when there are no points of
value left to play). In fact, when black has filled at c but not d,
the white string will be a peer of the two-eyed black group; a capture
at point a or b can then only be done once each by white and they then
become disallowed moves.
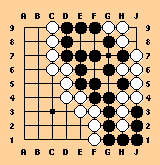
The official Japanese rules (1989) appear to have a problem in
relation to the following type of position, shown here on a 9 x 9
board with no prisoners and no compensation.
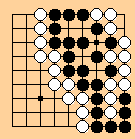
The question is whether Black can take the white group off the board without further play and win by one point (29-28). Most rulesets would say he can.
The 1989 Japanese rules, however, have a special rule for determining whether groups are alive at the end of the game. Under this special rule (not used during regular play), the only recognized ko threat is a pass. So if Black claims that White is dead, White will claim that Black is equally dead, offering the following proof.
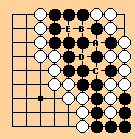
1. White A
2. Black B
3. White C
4. Black pass (can't recapture A because of the special rule)
5. White D
6. Black pass (no other move)
7. White E (removing all black stones)
By the 1989 Japanese rules, when both sides are dead, neither side can be taken off and the position is a seki.
The conclusion is that Black has to play another stone in
the original position, and the game ends in a 28-28 tie.
-- James Davies
From: rem@BTR.Com (Robert E. Maas)
Newsgroups: rec.games.go
Subject: Re: Problem in Japanese rules
Date: 16 Jun 1996 07:53:40 GMT
Organization: BTR Communications Company
Under Lasker/Maas rules, if both pass with white passing first, it's now white to play next during post-game dead-group-killing stage. White must play G7, else black responds by filling G7 then playing snapback at I8. (Or if white avoided snapback by playing G5 then I8, black can now retake at H5 then capture immediately at I9. That sequence is wG5 bG7 wI8 bH5 wPass bI9.) That gives:

Black must play F8 or else white will get two eyes by playing F8 then
G8. (F8-G8 isn't a ko yet, so bI8 can be answered by wI9, while bE8
can be answered by wG8, only if black got two moves in a row could
he both turn F8-G8 into a ko and make a ko threat at I8, which he wouldn't
need
of course.)

White must play G5, or else black gets two eyes by playing G5 himself.
But black can now play H7. It's a simple double-ko which black can't
lose. White can't stop black from filling at G7, giving black two eyes.
(If I overlooked any better line of play above, please let me know!)
If black passed first during regular play, so gets to play first during kill-dead-groups after-play, it's no problem, black just fills G7 and has two eyes immediately. Either way (regardless of who passed first), it's the same as if the players agreed to pick up all of white's dead stones and put them in black's prisoner pot, score: white=28-11=17 black=18, so black wins by 1 point.
Japanese rules of allowing white to claim he can kill black, because he can take both the ko at G7 and then the ko at G5 without black ever being able to take back, so white basically gets all the moves in a row and doesn't even have to fill a ko to prevent recapture ever, seem absurd to me.
DejaNews: ~a (rem@BTR.Com) & ~g (rec.games.go) & ~s (Lasker*)
2 Hits:
Date Scr Subject Newsgroup Author
1. 95/08/09 046 Lasker-Maas rules #1/3 rec.games.go rem@BTR.Com
2. 95/08/09 046 Lasker-Maas rules #1/2 rec.games.go rem@BTR.Com
From: Andre Engels <csg419@wing.rug.nl>
Newsgroups: rec.games.go
Subject: Re: Problem in Japanese rules
Date: Fri, 21 Jun 1996 13:19:03 +0200
Organization: Rijksuniversiteit Groningen
davies@tanuki.twics.com wrote:[elided]
What about the following change in the rules for ko in the second phase:
Does anyone see any problems with this change? I think there are,
although I can't see them yet. At least I see no problems that are
not
in the Japanese rules already (triple-ko etcetera).
Date: Fri, 05 Jul 1996 08:32:00 +0900
From: "GGA02126@niftyse" <GGA02126@niftyserve.or.jp>
Subject: Ko bestiary
To: wjh+@andrew.cmu.edu
[The] suggestion from Andre Engels in the Netherlands for a modification of the Japanese rules ... does not appear to give the right answer in the following position (9 x 9 board). The right answer, according to the Japanese rules, is that White is unconditionally dead in the top right, and the bottom left is a seki. The suggested modification, which allows a player to prohibit only one ko recapture per move in the life-and-death adjudication process, lets White trade the top right for the bottom left.

Black A2
White Pass (for A1)
Black H9
White J6
Black J8
White J9
Black H9 *
White A1 (for J9)
Black Pass (for A2)
White B4 (for J9)

Black A2
White A1 or J9, whichever Black permits,
prohibits Black's recapture on the next move
* The suggested rule has to be stated so that White can't prohibit
this
ko capture.
Regards,
James Davies GGA02126@niftyserve.or.jp