With M discrete memory storage slots, the problem then arises as to how
a specific training example should be generalized. Training examples are
represented here as ![]() , consisting of an angle
, consisting of an angle ![]() ,
an action a, and a result r where
,
an action a, and a result r where ![]() is the initial position
of the defender, a is ``s'' or ``p'' for ``shoot'' or ``pass,'' and
r is ``1'' or ``-1'' for ``goal'' or `` miss'' respectively. For
instance,
is the initial position
of the defender, a is ``s'' or ``p'' for ``shoot'' or ``pass,'' and
r is ``1'' or ``-1'' for ``goal'' or `` miss'' respectively. For
instance, ![]() represents a pass resulting in a goal for
which the defender started at position
represents a pass resulting in a goal for
which the defender started at position ![]() on its circle.
on its circle.
The most straightforward technique would be to store the result at the
single memory slot whose index is closest to ![]() , i.e., round
, i.e., round
![]() to the nearest
to the nearest ![]() for which Mem[
for which Mem[ ![]() ] is
defined, and then set
] is
defined, and then set ![]() . However, this technique does
not provide for the case in which we have two training examples
. However, this technique does
not provide for the case in which we have two training examples
![]() and
and ![]() , where
, where ![]() and
and ![]() both round to the same
both round to the same ![]() . In particular, there is no way of
scaling how indicative
. In particular, there is no way of
scaling how indicative ![]() is of
is of ![]() .
.
In order to combat this problem, we scale the value stored to
![]() by the inverse of the distance between
by the inverse of the distance between ![]() and
and
![]() relative to the distance between memory indices. A result
r at a given
relative to the distance between memory indices. A result
r at a given ![]() is multiplied by
is multiplied by ![]() before being stored to Mem[
before being stored to Mem[ ![]() ]. In this
way, training examples with
]. In this
way, training examples with ![]() 's that are closer to
's that are closer to ![]() can
affect Mem[
can
affect Mem[ ![]() ] more strongly. For example, with M = 18 (so
Mem[
] more strongly. For example, with M = 18 (so
Mem[ ![]() ] is defined for
] is defined for ![]() ),
), ![]() causes
causes
![]() to be updated by a value of
to be updated by a value of ![]() . Call this our basic memory storage
technique:
. Call this our basic memory storage
technique:
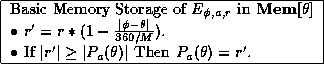
Using this generalization function, the ``update'' of ![]() would
only have an effect at all if
would
only have an effect at all if ![]() prior to this
training example. Consequently, only the past training example for
action a with
prior to this
training example. Consequently, only the past training example for
action a with ![]() closest to
closest to ![]() is reflected in
is reflected in
![]() : presumably, this training example is most likely to
accurately predict
: presumably, this training example is most likely to
accurately predict ![]() . Notice that this basic memory
storage technique is appropriate when the defender's motion is
deterministic. In order to handle variations in the defender's speed,
we introduce later a more complex memory storage technique. The
method of scaling a result based on the difference between
. Notice that this basic memory
storage technique is appropriate when the defender's motion is
deterministic. In order to handle variations in the defender's speed,
we introduce later a more complex memory storage technique. The
method of scaling a result based on the difference between ![]() and
and
![]() will remain unchanged.
will remain unchanged.
In our example above, ![]() would not only
affect Mem[120]: as long as
would not only
affect Mem[120]: as long as ![]() was not already larger,
its value would be set to
was not already larger,
its value would be set to ![]() .
Notice that any training example
.
Notice that any training example ![]() with
with ![]() could override this value. Since 116.5 is so much closer
to 120 than it is to 100, it makes sense that
could override this value. Since 116.5 is so much closer
to 120 than it is to 100, it makes sense that ![]() affects
Mem[120] more strongly than it affects Mem[100]. However,
affects
Mem[120] more strongly than it affects Mem[100]. However,
![]() would affect both memory values equally. This memory
storage technique is similar to the kNN and kernel regression function
approximation techniques which estimate
would affect both memory values equally. This memory
storage technique is similar to the kNN and kernel regression function
approximation techniques which estimate ![]() based on
based on ![]() possibly scaled by the distance from
possibly scaled by the distance from ![]() to
to ![]() for the k
nearest values of
for the k
nearest values of ![]() . In our linear continuum of defender
position, our memory generalizes training examples to the 2 nearest
memory locations.
. In our linear continuum of defender
position, our memory generalizes training examples to the 2 nearest
memory locations.![]()