Homework 4 (Due Sat 24-Sep at 8pm)

Important Notes:

Read the "Important Notes" at the top of hw1. The same general rules apply to all homework unless otherwise specified.
This homework is solo. You must not collaborate with anyone (besides current course TA's and faculty) in any way. See the syllabus for more details.
You will need these starter files:
1. hw4.py
2. cs112_f22_week4_linter.py
For this hw, you may submit up to 6 times, but only your last submission counts.
Do not use recursion this week, or any imports/data structures we have not yet covered.
Do not hardcode the test cases in your solutions.
As always, all your functions must be non-destructive unless the problem specifically indicates otherwise.
Also, if Python happens to provide a function that basically outright solves a problem, such as statistics.median() for the median problem below, do not use that function. Naturally, we are looking for you to write the core logic of the problem.

alternatingSum(a) [5 pts]
Write the function alternatingSum(a) that takes a list of numbers and returns the alternating sum (where the sign alternates from positive to negative or vice versa). For example, alternatingSum([5,3,8,4]) returns 6 (that is, 5-3+8-4). If the list is empty, return 0.

median(L) [5 pts]
Write the non-destructive function median(L) that takes a list of ints or floats and returns the median value, which is the value of the middle element of a sorted list, or the average of the two middle elements if there is no single middle element. If the list is empty, return None. Remember, do not use statistics.median() here, or any other functions/methods that basically solve the problem for you.

smallestDifference(L) [10 pts]
Write the function smallestDifference(L) that takes a list of integers and returns the smallest absolute difference between any two integers in the list. If the list has fewer than 2 elements, return -1. For example:
```
assert(smallestDifference([19,2,83,6,27]) == 4)
```
The two closest numbers in that list are 2 and 6, and their difference is 4.

nondestructiveRemoveRepeats(L) [5 pts]
Write the function nondestructiveRemoveRepeats(L), which takes a list L and nondestructively returns a new list in which any repeating elements in L are removed. For example:
```
assert(nondestructiveRemoveRepeats([1, 3, 5, 3, 3, 2, 1, 7, 5]) ==
                                   [1, 3, 5, 2, 7])
```
Also:
```
L = [1, 3, 5, 3, 3, 2, 1, 7, 5]
assert(nondestructiveRemoveRepeats(L) == [1, 3, 5, 2, 7])
assert(L == [1, 3, 5, 3, 3, 2, 1, 7, 5]) # nondestructive!
```
Note that the values in the resulting list occur in the order they appear in the original list, but each occurs only once in the result. Also, since this is a nondestructive function, it returns the resulting list.

destructiveRemoveRepeats(L) [5 pts]
Write the function destructiveRemoveRepeats(L), which implements the same function destructively. Thus, this function should directly modify the provided list to not have any repeating elements. Since this is a destructive function, it should not return any value at all (so, implicitly, it should return None). For example:
```
L = [1, 3, 5, 3, 3, 2, 1, 7, 5]
destructiveRemoveRepeats(L)
assert(L == [1, 3, 5, 2, 7]) # destructive!
```

isSorted(L) [15 pts]
Write the function isSorted(L) that takes a list of numbers and returns True if the list is sorted (either smallest-first or largest-first) and False otherwise. Your function must only consider each value in the list once (so, in terms of big-oh, which we will learn soon, it runs in O(n) time, where n=len(L)), and so in particular you may not sort the list.

runLengthEncode(dataList) [15 pts]
First, you can read about run-length encoding and compression here. Then, write the function runLengthEncode(dataList) that takes a list of numbers and returns a list of numbers that results from "reading off" the initial list, using tuples for each (count, value) pair. This is similar to the look-and-say method. For example:
```
runLengthEncode([]) == []
runLengthEncode([1,1,1]) == [(3,1)]
runLengthEncode([-1,2,7]) == [(1,-1),(1,2),(1,7)]
runLengthEncode([3,3,8,-10,-10,-10]) == [(2,3),(1,8),(3,-10)]
runLengthEncode([3,3,8,3,3,3,3]) == [(2,3),(1,8),(4,3)]
```
Understanding the following is not necessary for completing this problem. However, if you are curious, run-length encoding on files does not always result in smaller file sizes, and works best for data with long runs of repeated values (like simple black-and-white images, for example).
Since each tuple in a run-length-encoded list contains two values, we can approximate the compression ratio for a paritcular list like so:
```
def compressionRatio(uncompressedList):
    rle = runLengthEncode(uncompressedList)
    return len(uncompressedList)/(len(rle)*2)

print(compressionRatio([3,3,8,3,3,3,3]))
```
A higher compression ratio is preferable. If the compression rate is less than 1, however, the run-length-encoded list contains more values than the original list. For example:
```
print(compressionRatio([3,1,4,1,5,9,2])) # Prints 0.5!
```
Lastly, on the subject of compression, you may find this paper interesting! The segmentation mask (right) is stored as 640,000 integers with values 0 to 6, representing the label for each pixel. Using our runLengthEncode function, we can compress this down to only 26,098 integers, a compression ratio of 24.5:1, 0.04078 times the original size.

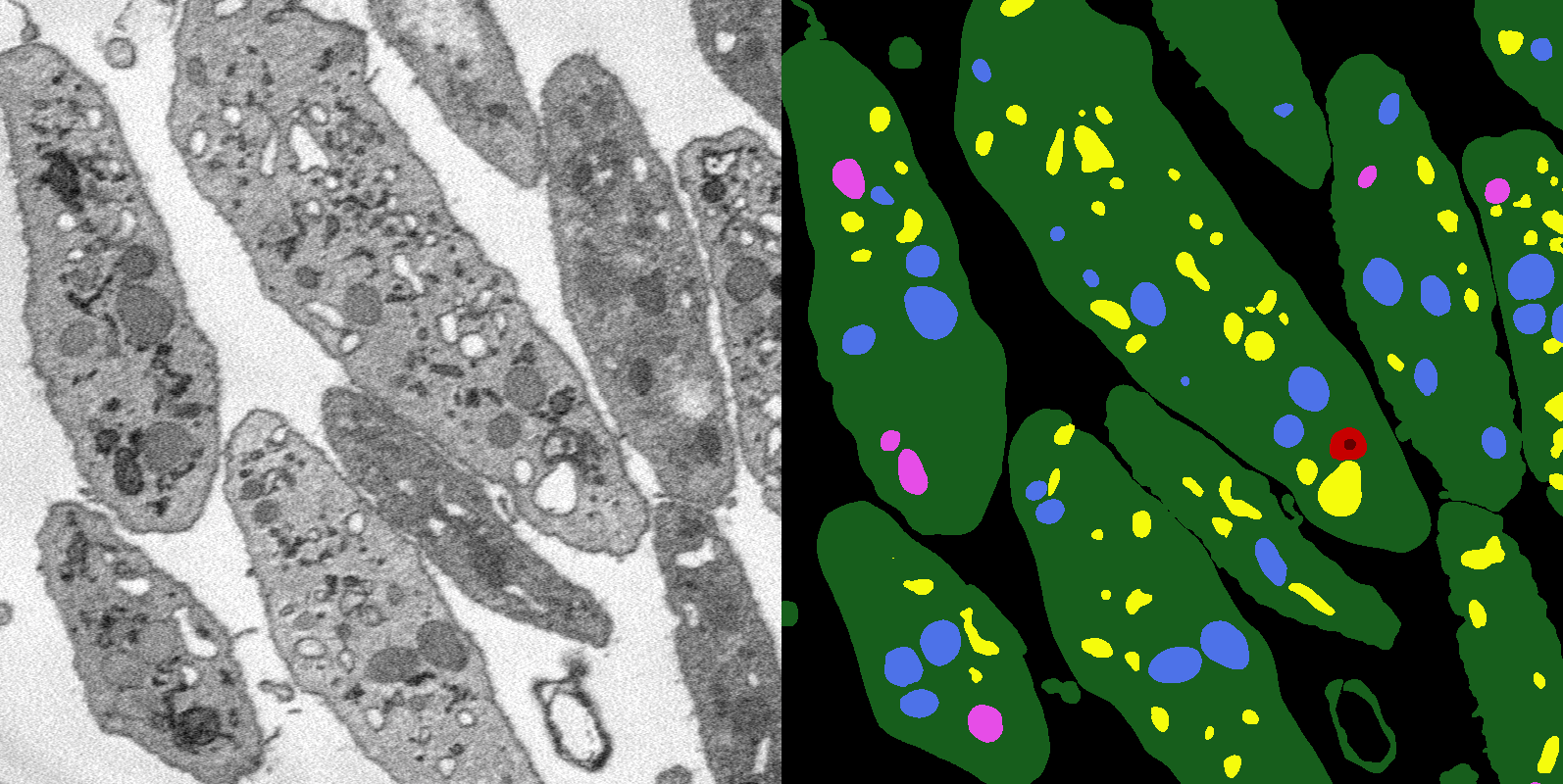
runLengthDecode(rleList) [10 pts]
Write the function runLengthDecode(rleList) that does the inverse of the previous problem, so that, in general:
```
runLengthDecode(runLengthEncode(dataList)) == dataList
```
Or, in particular:
```
runLengthDecode([(2,3),(1,8),(3,-10)]) == [3,3,8,-10,-10,-10]
```

multiplyPolynomials(p1, p2) [15 pts]
Background: we can represent a polynomial as a list of its coefficients. For example, [2, 3, 0, 4] could represent the polynomial 2x³ + 3x² + 4. With this in mind, write the function multiplyPolynomials(p1, p2) which takes two lists representing polynomials as just described, and returns a third list representing the polynomial which is the product of the two.

For example:
multiplyPolynomials([2,0,3], [4,5]) represents the problem (2x**2 + 3)(4x + 5), and:
(2x**2 + 3)(4x + 5) = 8x**3 + 10x**2 + 12x + 15
And so this returns the list [8, 10, 12, 15].

bestScrabbleScore(dictionary, letterScores, hand) [15 pts]
Background: in a Scrabble-like game, players each have a hand, which is a list of lowercase letters. There is also a dictionary, which is a list of legal words (all in lowercase letters). And there is a list of letterScores, which is length 26, where letterScores[i] contains the point value for the ith character in the alphabet (so letterScores[0] contains the point value for 'a'). Players can use some or all of the tiles in their hand and arrange them in any order to form words. The point value for a word is 0 if it is not in the dictionary; otherwise it is the sum of the point values of each letter in the word, according to the letterScores list (pretty much as it works in actual Scrabble).

In case you are interested, here is a list of the actual letterScores for Scrabble:
```
letterScores = [
#  a, b, c, d, e, f, g, h, i, j, k, l, m,
   1, 3, 3, 2, 1, 4, 2, 4, 1, 8, 5, 1, 3,
#  n, o, p, q, r, s, t, u, v, w, x, y, z
   1, 1, 3,10, 1, 1, 1, 1, 4, 4, 8, 4,10
]
```
Note that your function must work for any list of letterScores that is provided by the caller.

With this in mind, write the function bestScrabbleScore(dictionary, letterScores, hand) that takes 3 lists -- dictionary (a list of lowercase words), letterScores (a list of 26 integers), and hand (a list of lowercase characters) -- and finds the highest-scoring word in the dictionary that can be formed by some arrangement of some set of letters in the hand.
- If there is only one highest-scoring word, return it and its score in a tuple.
- If there are multiple highest-scoring words, return a tuple with two elements: a list of all the highest-scoring words in the order they appear in the dictionary, then the score.
- If no highest-scoring word exists (ie, if no legal words can be formed from the hand), return None instead of a tuple.
The dictionary in this problem is a list of words, and thus not a true Python dictionary (which we haven't taught you and you may not use in this assignment)! It is ok to loop through the dictionary, even if the dictionary we provide is large.

Hint: You should definitely write helper functions for this problem! In fact, try to think of at least two helper functions you could use before writing any code at all.

Another Hint: You may not use itertools for this problem! In fact, do not create permutations of the letters at all -- that is, do not try to generate all the possible ways to arrange the hand! If you do, your solution will take too long and Autolab will time out (hence, fail). There's a much simpler way to find all the legal words you can create...

Yet one more hint: Consider: if you had a single word, and you have a single hand, could you write a function f(word,hand) (perhaps with a better name) that tells you whether or not that word could be constructed using that hand? And how might you use that function to help solve this problem?

Bonus/Optional: linearRegression(pointsList) [2 pts]
Write the function linearRegression(poinstList) that takes a list of (x,y) points and finds the line of best fit through those points. Specifically, your function should return a triple of floats (a,b,r) such that y = ax+b is the line of best fit through the given points and r is the correlation coefficient as explained here (and yes, you must follow this exact approach). For example (taken from the text), linearRegression([(1,3), (2,5), (4,8)]) should return a triple of 3 values approximately equal to (1.6429, 1.5, 0.9972), indicating that the line of best fit is y = 1.6429x + 1.5, with a correlation coefficient of 0.9972 (so it's a really good fit, too). Note that the result is approximately equal to these values. Also note: the notes we refer you to do not discuss the meaning of the sign of r, so just return the absolute value |r|. And: you may ignore the case of a vertical line in your linearRegression code.

Bonus/Optional: runSimpleProgram(program, args) [2 pts]
First, carefully watch this video that describes this problem:

Then, write the function runSimpleProgram(program, args) that works as described in the video, taking a legal program (do not worry about syntax or runtime errors, as we will not test for those cases) and runs it with the given args, and returns the result.

Here are the legal expressions in this language:
- [Non-negative Integer]
  Any non-negative integer, such as 0 or 123, is a legal expression.
- A[N]
  The letter A followed by a non-negative integer, such as A0 or A123, is a legal expression, and refers to the given argument. A0 is the value at index 0 of the supplied args list. It is an error to set arg values, and it is an error to get arg values that are not supplied. And you may ignore these errors, as we will not test for them!
- L[N]
  The letter L followed by a non-negative integer, such as L0 or L123, is a legal expression, and refers to the given local variable. It is ok to get an unassigned local variable, in which case its value should be 0.
- [operator] [operand1] [operand2]
  This language allows so-called prefix expressions, where the operator precedes the operands. The operator can be either + or -, and the operands must each be one of the legal expression types listed above (non-negative integer, A[N] or L[N]).
And here are the legal statements in this language (noting that statements occur one per line, and leading and trailing whitespace is ignored):
- ! comment
  Lines that start with an exclamation (!), after the ignored whitespace, are comments and are ignored.
- L[N] [expr]
  Lines that start with L[N] are assignment statements, and are followed by the expression (as described above) to be stored into the given local variable. For example: L5 - L2 42 This line assigns (L2 - 42) into L5.
- [label]:
  Lines that contain only a lowercase word followed by a colon are labels, which are ignored except for when they are targets of jump statements.
- JMP [label]
  This is a jump statement, and control is transferred to the line number where the given label is located. It is an error for such a label to not exist, and you may ignore that error.
- JMP+ [expr] [label]
  This is a conditional jump, and control is transferred to the line number where the given label is located only if the given expression is positive. Otherwise, the statement is ignored.
- JMP0 [expr] [label]
  This is another kind of conditional jump, and control is transferred only if the given expression is 0.
- RTN [expr]
  This is a return statement, and the given expression is returned.
Hints:
1. Do not try to translate the program into Python! Even if you could do so, it is not allowed here. Instead, you are going to write a so-called interpreter. Just keep track of the local variables, and move line-by-line through the program, simulating the execution of the line as appropriate.
2. You will find it useful to keep track of the current line number.
3. How long do you run the program? Until you hit a RTN statement! You may assume that will always eventually happen.
4. We used strip, split, and splitlines in our sample solution, though you of course may solve this how you wish.
Finally, here is a sample test function for you. You surely will want to add some addition test cases. In fact, a hint would be to build your function incrementally, starting with the simplest test cases you can think up, which use the fewest expression and statement syntax rules. Then add more test cases as you implement more of the language.
def testRunSimpleProgram(): print("Testing runSimpleProgram()...", end="") largest = """! largest: Returns max(A0, A1) L0 - A0 A1 JMP+ L0 a0 RTN A1 a0: RTN A0""" assert(runSimpleProgram(largest, [5, 6]) == 6) assert(runSimpleProgram(largest, [6, 5]) == 6) sumToN = """! SumToN: Returns 1 + ... + A0 ! L0 is a counter, L1 is the result L0 0 L1 0 loop: L2 - L0 A0 JMP0 L2 done L0 + L0 1 L1 + L1 L0 JMP loop done: RTN L1""" assert(runSimpleProgram(sumToN, [5]) == 1+2+3+4+5) assert(runSimpleProgram(sumToN, [10]) == 10*11//2) print("Passed!")