Lab Week 05 - Fall 2024

Tuesday, September 24, 2024

Introduction

Remember: As you work on these steps with guidance from your teaching assistant, you should look toward your neighbor to see if they need help (or ask if you need help). You can collaborate in lab during these activities!

In this lab, you will

• Practice programming with polar coordinates.
• Use a separate user-defined function to draw multiple rotating patterns on the canvas.

Create a folder named lab-05 for this lab in your 15-104 folder/directory.

Here is a link to the p5.js template we are using to create the program.

template2023-p5only.zip

NOTE: Unlike previous labs, you will create just one program in this lab, modifying it as you go along through the exercises. After each exercise, you will make a copy of the lab-05 folder, with a different name, just in case you mess things up terribly. If so, you can go back to your prior working program.

Problem A: Rotating Circle using Polar Coordinates

Write a p5.js program that displays a yellow circle of diameter 25, rotating clockwise around the center of a 400 X 400 canvas at a distance of 50 from the center of the canvas.

• Create a global variable that stores the angle of where the circle will be drawn with respect to the center of the canvas.
• In the sketch.js file, update the setup function to use a 400 X 400 canvas.
• In the draw function, complete the code so that one yellow circle of diamter 25 is drawn at a distance of 50 at the current angle with respect to the center of the canvas.
  • It will pay off to translate the origin to the center before you draw.
  • Do NOT use the rotate function. Instead, think in polar coordinates, using cos and sin to find the correct place to draw the circle.
  • At the end of the draw function, update your variable that stores the angle by increasing it by a small amount (e.g. 2). (The higher this number is, the faster the circle will rotate around the center.)
  • Do not set the background color back to gray each time, so you can see all of the circles.

Once you are done, you should see the circle rotating around the center, as shown by this snapshot:

Problem B: Using a User-defined function

BEFORE YOU START THIS STEP, SAVE A COPY OF YOUR CURRENT WORKING lab-05 FOLDER UNDER ANOTHER NAME (e.g. lab-05-partA) IN CASE YOU NEED TO START THIS PROBLEM AGAIN

Modify your sketch.js in the lab-05 folder so that the same picture is drawn but you draw the circle in a separate function called spinningCircle.

• Write this new function after the draw function (i.e. after the curly right bracket).
• This function should have two parameters x and y that indicate the center location of where the circle will be drawn.
• Move the instructions that draw the circle into the new function. If any part of the moved code depends on x and y, change those values to these variables.
• Back in the draw function, put a call to the new function where you removed the code, including two arguments for the values x and y in the new function.

If you do this correctly, you should see the same drawing when you run the program as you had in part A.

Problem C: Multiple spinning circles

BEFORE YOU START THIS STEP, SAVE A COPY OF YOUR CURRENT WORKING lab-05 FOLDER UNDER ANOTHER NAME (e.g. lab-05-partB) IN CASE YOU NEED TO START THIS PROBLEM AGAIN

Modify your draw function so that it draws three of these rotating patterns, centered around (100, 100), (300, 100) and (200, 300).

• You should be able to just replace the single call to the spinningCircle function with three calls with appropriate arguments.
• Note: since your spinningCircle function uses translate to move to a new "origin", if you call this function multiple times, these translations will accumulate unless you use push and pop.

If you get this working correctly, you should see something like this snapshot:

Problem D: Grid of rotating circles

BEFORE YOU START THIS STEP, SAVE A COPY OF YOUR CURRENT WORKING lab-05 FOLDER UNDER ANOTHER NAME (e.g. lab-05-partC) IN CASE YOU NEED TO START THIS PROBLEM AGAIN

Modify your program so that it draws a grid of 16 of these rotating circles. Use nested loops to solve this problem, rather than writing 16 separate function calls. Your solution should have just one function call used 16 times.

Here are the coordinates of the "origins" for each of the rotations:

  (50,  50), (150,  50), (250,  50), (350,  50)
  (50, 150), (150, 150), (250, 150), (350, 150)
  (50, 250), (150, 250), (250, 250), (350, 250)
  (50, 350), (150, 350), (250, 350), (350, 350)
  

If you get this working correctly, you should see something like this snapshot:

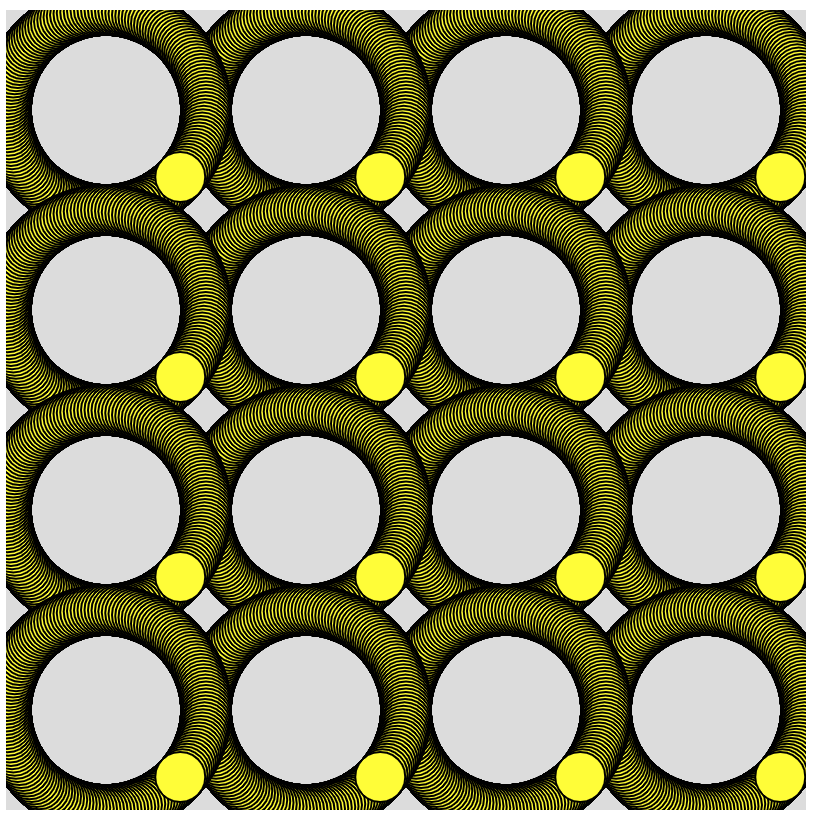
Problem E: Grid of rotating circles of a random color

BEFORE YOU START THIS STEP, SAVE A COPY OF YOUR CURRENT WORKING lab-05 FOLDER UNDER ANOTHER NAME (e.g. lab-05-partD) IN CASE YOU NEED TO START THIS PROBLEM AGAIN

Finaly modify your program so that it draws a grid of 16 of these rotating circles in a random color of these 8 colors:

  black    (0, 0, 0)
  red      (255, 0, 0)
  green    (0, 255, 0)
  blue     (0, 0, 255)
  cyan     (0, 255, 255)
  magenta  (255, 0, 255)
  yellow   (255, 255, 0)
  white    (255, 255, 255)

All sixteen rotating patterns will be drawn with the same color. If you reload the page, some random color of these 8 is chosen to draw the patterns. Can you solve this without using if/else statements? Here are two sample runs of the program:

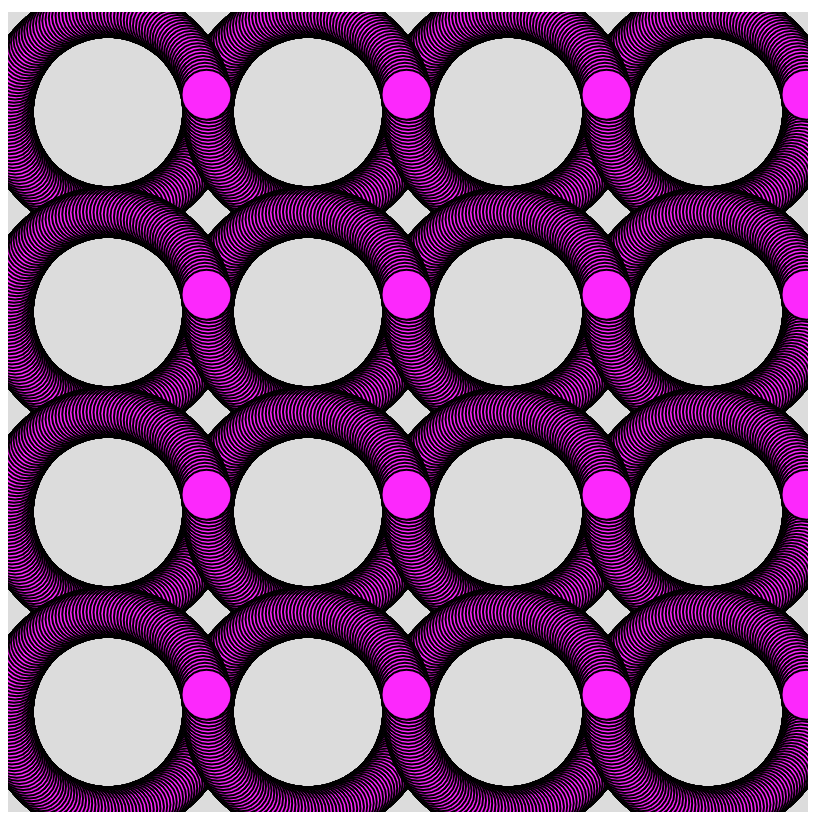
FUN CHALLENGE: Get squares instead of circles to rotate around these 16 points, so that the squares themselves also rotate to align with the circular path, rather than having the squares move around always aligned with the canvas.

(Now you might need to use the rotate function.)

Once you run out of time, you should submit your final completed work for credit.

• Compress your final working lab-05 folder into a zip file.
• Hand in the compressed file to Autolab in the Lab 05 assessment location.
• REMEMBER to check what you submitted in Autolab by looking at the submission file. (Do this for the deliverables too!)