[4 points] Recall that, one way to represent the nodes of a complete binary tree is with an array, where the first element contains the root, the next two elements contain the next level of the tree (the children of the root), the next four elements contain the next level of the tree (two containing the children of the root's left child and two containing the children of the root's right child), the next eight elements contain the next level (the two children of each of the nodes at the previous level), and so on, depending on how many levels the tree has.

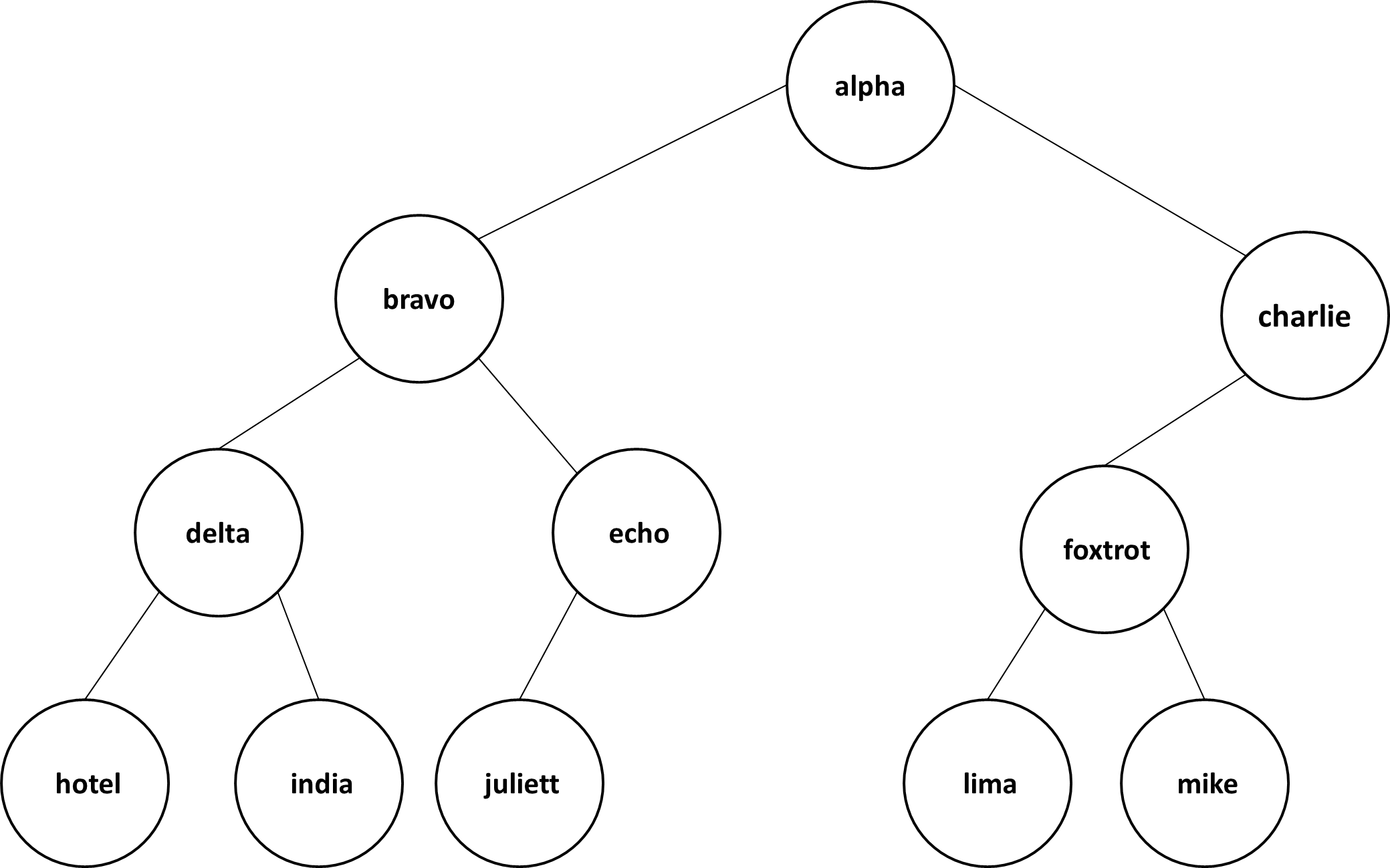
The binary tree above with nodes labeled with strings "alpha", "bravo", ... would be represented by the Ruby array:
["alpha", "bravo", "charlie", "delta", "echo", "foxtrot", "golf", "hotel", "india", "juliet", "kilo", "lima", "mike", "nova", "oscar"]
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Let us look at the indices of left children:
-
The node at 0 has its left child at 1 (alpha's left child is bravo)
The node at 1 has its left child at 3 (bravo's left child is delta)
The node at 2 has its left child at 5 (charlie's left child is foxtrot)
The node at 3 has its left child at 7 (delta's left child is hotel)
The node at 4 has its left child at 9 (echo's left child is juliet)
Do you see a pattern? There are simple formulas that can be used to calculate the indices of a node's left child, right child, and parent from that node's index.
Define a function left_index(index) (in left_index.rb) that, when passed the index of a node, will return the index of that node's left child. (You do not need to worry about whether the node has a left child; when the node does not actually have a left child, the function should still return where its left child would be if it had one. You may assume that index is a non-negative integer.)
Define a function right_index(index) (in
right_index.rb) that, when passed the index of a node,
will return the index of that node's right child.
(You do not need to worry about whether the node has a right
child; when the node does not actually have a right child, the
function should still return where its right child would
be if it had one. You may assume that
Define a function parent_index(index) (in parent_index.rb) that, when passed the index of a node, will return the index of that node's parent. (You may assume that the index is a positive integer.)
Define a function leaf?(tree, index) (in leaf.rb ) that, when passed the array representation tree of a complete binary tree and the index of a node index, will return true if the node has no children and false otherwise (a node with no children is called a leaf). You may assume that index is a non-negative index less than the length of tree . You may want to use some of the functions you defined in the previous parts.
Example usage:
>> a = ["alpha", "bravo", "charlie", "delta", "echo", "foxtrot", "golf", "hotel", "india", "juliett", "kilo", "lima", "mike", "nova", "oscar"]
=> ["alpha", "bravo", "charlie", "delta", "echo", "foxtrot", "golf", "hotel", "india", "juliett", "kilo", "lima", "mike", "nova", "oscar"]
>> leaf?(a,0)
=> false
>> leaf?(a,13)
=> true
The array representation for binary trees can be extended to incomplete trees by using nil to represent the "missing" nodes that would need to be added to make a complete tree.
For example, the binary tree above can be represented by the Ruby array
["alpha", "bravo", "charlie", "delta", "echo", "foxtrot", nil , "hotel", "india", "juliett", nil, "lima", "mike", nil , nil ]
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Note that since missing children can always be represented by nil, the
tree ["alpha"] is the same as the tree ["alpha", nil,
nil].
- If the node with index i does not have any children then return 0. Else do the following:
- Return the sum of left_sum and right_sum.
- [2 points] (corrected) In file missing_child.rb write a recursive
function missing_child(tree,i) that searches the subtree
beginning at node i and returns a list of the labels of the
nodes that have only one child. In defining
missing_child(tree,i) you may want to make use of some of the
functions you defined in Question 1.
Example usage:
>> a = ["alpha", "bravo", "charlie", "delta", "echo", "foxtrot", nil, "hotel", "india", "juliet", nil, "lima", "mike", nil, nil] => ["alpha", "bravo", "charlie", "delta", "echo", "foxtrot", nil, "hotel", "india", "juliett", nil, "lima", "mike", nil, nil] >> missing_child(a, 0) => ["echo", "charlie"] >> missing_child(a, 1) => ["echo"] >> missing_child(a, 2) => ["charlie"] >> b = ["apple", "banana", "cherry", nil, "date", nil, nil] => ["apple", "banana", "cherry", nil, "date", nil, nil] >> missing_child(b, 0) # draw the tree b to check the answer => ["banana"] >> c = ["aardvark", "bear", nil, "cat", "dog", nil, nil, "eel", nil] => ["aardvark", "bear", nil, "cat", ""dog", nil, nil "eel", nil] >> missing_child(c, 0) # draw the tree c to check the answer => ["aardvark", "cat"]You should solve this problem in stages:- What is the base case? What value should be returned in that case? Write code that handles this base case.
- Test your program on the tree ["aardvark"] with initial index 0; the result should be [].
- What is the recursive case? How should you combine the results of the recursive calls? Add code to handle this case.
- You should get the same result for the tree ["aardvark", nil, nil] as for the tree ["aardvark"]. Do you see why?
- Test your program on the tree ["aardvark", "bear", nil]. The result shold be ["aardvark"].
- Test your program on the tree ["aardvark", "bear", "cat"]. The result should be []. Draw this tree.
- Test your program on the tree ["aardvark", "bear", nil, "cat"]. The result should be ["aardvark", "bear"].
- Test your program on the tree ["aardvark", "bear", "cat", nil, "dog"]. The result should be ["bear"].
- If your program fails one of these tests, figure out how to change the code to fix the problem, and re-run all the preceding tests to make sure they still work.
- It might help to put the statements print i, " "; p tree at the beginning of your function so you can trace the recursive calls.
- Continue adding tests until you are confident your program is correct.
[1 point] The descendants of a node \(p\) in a tree are defined to include all the nodes that are on a path from the node \(p\), excluding \(p\) itself. For example, in the incomplete tree above, the descendants of the node with label "charlie" consist of the nodes with labels "foxtrot", "lima", and "mike". In this question you will write a recursive function num_descendants(tree,i), which requires an array tree encoding a binary tree as described above and an index i of a node in the binary tree. When called, num_descendants(tree,i) should return the number of descendants of the node at index i.
The following algorithm counts the number of descendants of the node at index i in the array tree, which is an array representation of a non-empty, possibly incomplete binary tree.
-
If the node with index i has a left child, then
set left equal to the index of that
child. Recursively, count the descendants of left
and set left_sum to 1 plus the result of this
recursive call. Otherwise (i.e., when the node doesn't
have a left child), set left_sum to zero.
If the node with index i has a right child,
then set right equal to the index of that
child. Recursively, count the descendants of right,
and set right_sum to 1 plus the result of this
recursive call. Otherwise (i.e., when the node doesn't
have a right child), set right_sum to zero.
In num_descendants.rb, using the algorithm above, define a function num_descendants(tree,i), which requires an array tree encoding a binary tree as described above and an index i of a node in the binary tree. When called, num_descendants(tree,i) should return the number of descendants of the node at index i. You can assume that the function will always be called with a "correct" array representation, so if a node is nil, the array entries where its children would be located will also be nil.
Example usage:>> num_descendants(a,0) # alpha has 10 descendants => 10 >> num_descendants(a,2) # charlie has 3 descendants => 3 >> num_descendants(a,7) # hotel has no descendants => 0
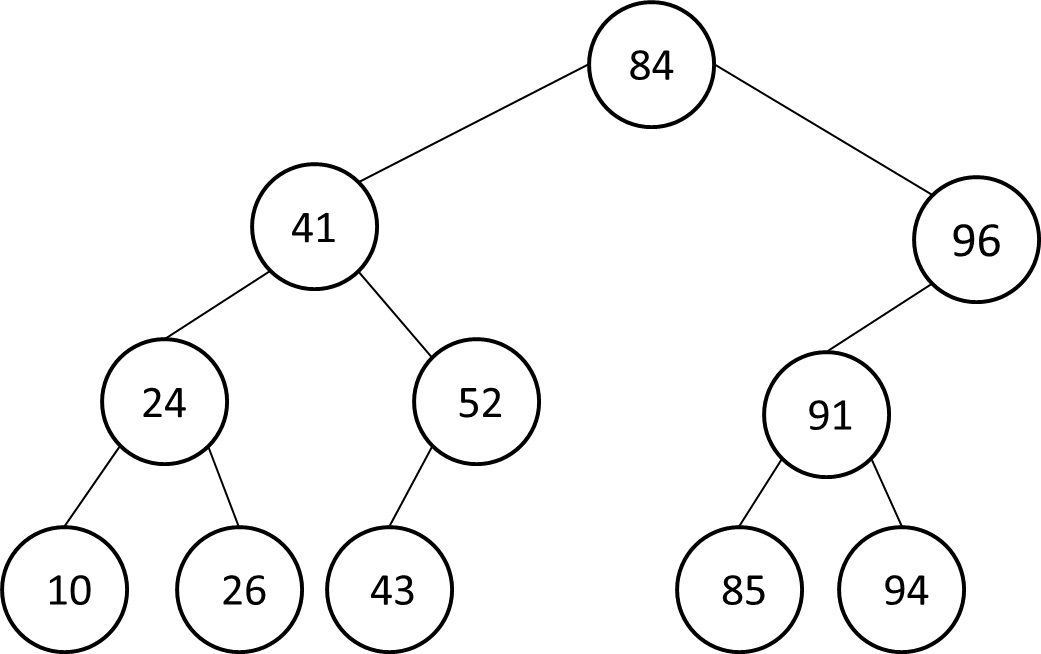
[2 points] In a Binary Search Tree, each node has a value that is greater than that of all of the nodes reachable through its left child and that is less than that of all of the nodes reachable through its right child. The examples below is a binary search tree. (We will assume that the tree does not hold two nodes with the same value.)
A Binary Search Tree can be stored using an array just as we did in the previous problems.
The following is an algorithm for searching an array tree encoding a binary search tree to determine whether it contains a node with the value key.
-
Set curr_index to the index of the root node of the tree.
While curr_index is less than the length of tree
and tree[curr_index] is not nil,
do the following:
-
Set curr_value to the value of the node at
curr_index in tree.
Return true if curr_value is equal to key.
Set curr_index to the index of the left child
of the node at curr_index if key is less than
curr_value.
Set curr_index to the index of the right child
of the node at curr_index if key is greater than
curr_value.
Define a function bst_search?(tree,key) (in bst_search.rb) that uses this algorithm to determine whether the value key occurs in tree, the array representing a binary search tree. Call the functions left_index and right_index that you defined in problem 1 to set curr_index in substeps C and D above.
Example usage:
>> bstree = [84,41,96,24,52,91,98,10,26,43,nil,85,94,nil,nil]
=> [84,41,96,24,52,91,98,10,26,43,nil,85,94,nil,nil]
>> bst_search?(bstree, 52)
=> true
>> bst_search?(bstree, 51)
=> false
>> bst_search?(bstree, 41)
=> true
>> bst_search?(bstree, 97)
=> false
[1 point] (corrected) Recall that a graph of \(n\) nodes can be represented as an \(n \times n\) matrix where the value at row \(i\) column \(j\) gives the "cost" of going directly from node \(i\) to node \(j\) in the graph.
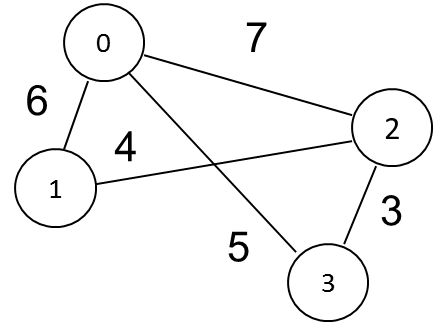
In file min_local.rb write a Ruby function min_local(g,index) that, when passed a graph g and index returns the minimum cost of going from the node with index directly to another node.
Hints:
You can represent infinite edge weights by
using the expression 1.0/0.0 which evaluates to
a special floating point number that is treated as being
larger than any other floating point number (i.e. infinity).
Use this inf value to represent the weight of going from a node to itself.
Example usage:
>> inf = 1.0/0.0 => Infinity >> G = [[inf,6,7,5], [6,inf,4,inf], [7,4,inf,3], [5,inf,3,inf]] => [[Infinity,6,7,5], [6,Infinity,4,Infinity], [7,4,Infinity,3], [5,Infinity,3,Infinity]] >> min_local(G, 0) => 5 >>min_local(G,2) => 3