Propositional Logic and SAT
Learning Objectives
-
Define the following logic terms and apply them to real-world problems:
-
Model
-
Knowledge Base
-
Query
-
Entailment
-
Satisfiability
-
-
Define the following propositional logic terms
-
Symbol
-
Literal
-
Operator
-
Sentence
-
Clause
-
Definite Clause
-
Horn Clause
-
-
Determine whether a knowledge base entails a query
-
Determine whether a given model satisfies a query
-
Compute whether a sentence is satisfiable
-
Describe the simple model checking algorithm and the theorem proving algorithms - forward chaining and resolution, what they compute, and understand runtime and space requirements
-
Define soundness and completeness for model checking and theorem proving algorithms
-
Describe the definition of (Boolean) satisfiability problems (SAT)
-
Describe conjunctive normal form (CNF) and why it is required for certain algorithms
-
Implement successor-state axioms to encode the logic for how fluents change over time
-
Describe and implement SAT Plan (planning as satisfiability) to real-world problems
Logical Agents
If we create a set of variables representing each of the statements that we would like to verify
and a set of variables to our starting conditions, we can search all assignments of values to
variables and check if our goal condition is ever true.
Alternatively, we can use logical statements to help us infer new variable values from starting
conditions (inference).

Main Idea: The agent encodes percepts that it receives as logical statements
that are added to a knowledge base of logical rules and facts. The agent then reasons about what
to do based on the knowledge base.
Vocab
-
Model: A complete assignment of symbols to True or False
-
Sentence: Logical statement composed of logical symbols and operators
-
Knowledge Base: Collection of sentences representing what we know about the world. The sentences are effectively all AND-ed together.
-
Query: Sentence we want to know is definitely true, definitely false, or unknown
Propositional Logic
-
Symbols: Variables that can be true or false (Note: usually represented by capital letters).
-
Operators
-
\(\neg A\): Not \(A\) (Negation)
-
\(A \wedge B\): \(A\) and \(B\) (Conjunction)
-
\(A \vee B\): \(A\) or \(B\) (Disjunction) - inclusive rather than exclusive or
-
\(A \Rightarrow B\): \(A\) implies \(B\) (Implication)
-
\(A \Leftrightarrow B\): \(A\) if and only if \(B\) (Biconditional)
-
-
Sentence: defined constructively as
Base Case:-
A symbol (e.g. \(X\)) is a sentence
Recursive Cases:
-
If \(A\) is a sentence, \(\neg A\) is a sentence
-
If \(A, B\) are sentences, \(A \wedge B\) is a sentence
-
If \(A, B\) are sentences, \(A \vee B\) is a sentence
-
If \(A, B\) are sentences, \(A \Rightarrow B\) is a sentence
-
If \(A, B\) are sentences, \(A \Leftrightarrow B\) is a sentence
-
-
Literal: an atomic sentence. \(True, False, A, \neg A\) (where \(A\) is a symbol) are literals.
-
Clause: a disjunction of literals. Two clauses: \(\alpha_1: A \vee \neg B \vee \neg C\), \(\alpha_2: A \vee B \vee \neg C\).
-
A definite clause is a clause with exactly one positive (i.e. not negated) literal. \(\alpha_1\) is a definite clause while \(\alpha_2\) is not.
-
A Horn clause is a clause with at most one positive literal. \(\alpha_1\) is a horn clause and \(\alpha_2\) is not.
-
-
Conjunctive Normal Form (CNF): a conjunction of one or more clauses. For instance, \(\alpha_1 \wedge \alpha_2\) is a sentence in CNF. One way to think of this is an AND of ORs.
Converting Propositional Logic to CNF
Many algorithms and solvers require the logic to be in CNF. It is useful to know how to convert any propositional logic sentence into CNF. Here are some rules that can be useful to convert the sentence into the correct form. (We are assuming \(\alpha, \beta, \gamma\) are some generic sentences):
-
\(\alpha \Leftrightarrow \beta \equiv (\alpha \Rightarrow \beta) \wedge (\beta \Rightarrow \alpha)\) [Biconditional Elimination]
-
\(\alpha \Rightarrow \beta \equiv \neg \alpha \lor \beta\) [Implication Elimination]
-
\(\neg (\alpha \land \beta) \equiv \neg \alpha \lor \neg \beta\) [DeMorgan's Law]
-
\(\alpha \lor (\beta \land \gamma) \equiv (\alpha \lor \beta) \land (\alpha \lor \gamma)\) [Distribute \(\lor\) over \(\land\)]
As an exercise, try to create the truth tables to see why these rules work. Try writing any proposition logic sentence and see if you can get it into CNF.
Entailment
Entailment (\(\alpha \vDash \beta\)): \(\alpha\) entails \(\beta\) iff for every model that causes \(\alpha\) to be true, \(\beta\) is also true. In other words, the \(\alpha\)-models (models that cause \(\alpha\) to be true) are a subset of the \(\beta\)-models (models(\(\alpha\)) \(\subseteq\) models(\(\beta\))).
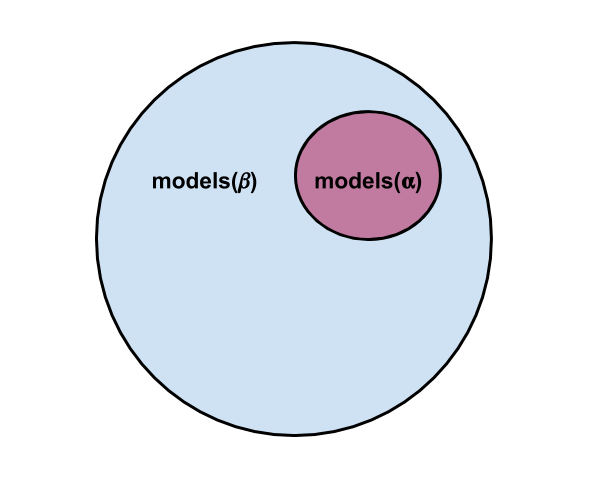
Properties:
-
Sound: Everything it claims to prove is entailed
-
Complete: Every sentence that is entailed can be proved
Usually, we want to know whether the knowledge base entails a specific query. To prove this entailment, two main methods are used, model checking and theorem proving.
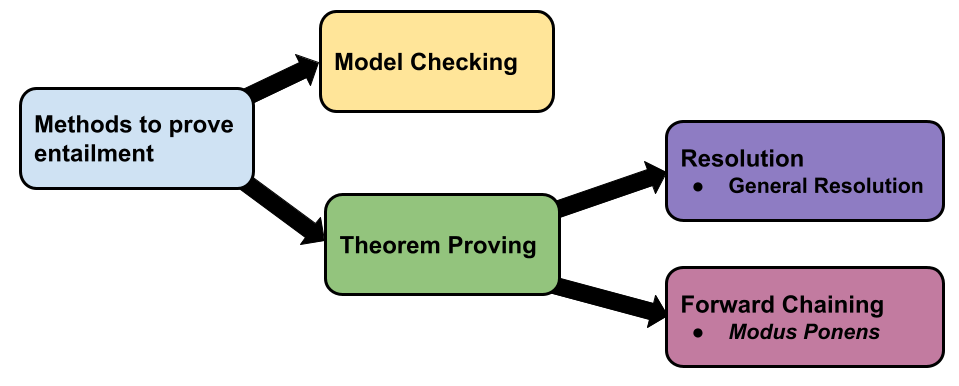
Model Checking
(Simple) Model checking basically enumerates all possible models and checks that for every model
that makes the KB sentence true, the query is also true. You can think of this as using truth
table to prove entailment.
As anyone who's constructed a truth table with \(\ge 3\)
variables knows, this is a reliable (sound and complete) yet wildly inefficient method, running
in exponential time with respect to the number of symbols.
Theorem Proving
Two key inference rules used in theorem proving algorithms are:
-
Modus Ponens: Given \(X_1 \land X_2\land... \land X_n \Rightarrow Y\) and \(X_1 \land X_2... \land X_n\), infer \(Y\).
-
General resolution: Given \(A_1 \lor A_2 \lor \lnot B\) and \(B \lor C_1 \lor C_2\), infer \(A_1 \lor A_2 \lor C_1 \lor C_2\) (law of excluded middle - we know \(B\) must be either \(True\) or \(False\), so if both these sentences are true, either \((A_1 \lor A_2)\) or \((C_1 \lor C_2)\) must be true).
Resolution and forward chaining are two algorithms used for theorem proving. As the name suggests, the resolution algorithm uses resolution inference rule, and forward chaining uses Modus Ponens inference rule.
Resolution Algorithm
\(KB \vDash \alpha\) means for all models that make the \(KB\) true, \(\alpha\) is also
true. This is equivalent to saying there does not exist any model such that \(KB \land \lnot \alpha\) is true. We can prove \(KB \land \lnot \alpha\) is unsatisfiable through proof by
contradiction.
We start with CNF clauses, including clauses in the KB and \(\lnot \alpha\). Then, we repeatedly use general resolution to resolve pairs of clauses until you resolve an empty clause, i.e., \(E \land \lnot E \Rightarrow False\). When that happens it means that \(KB \land \lnot \alpha\) is unsatisfiable. Therefore, we know \(KB \vDash \alpha\). On the other hand, if we run out of possible pairs of clauses to resolve and never resolved an empty clause, then the KB does not entail \(\alpha\).
The resolution algorithm is sound and complete for any propositional logic (PL) KBs, but its runtime complexity is exponential with respect to the number of symbols. Note that the PL KB must be converted to CNF first, but that's no problem since any PL sentence can be converted to CNF.
Example
KB = \(P, \lnot P \lor Q, P \lor \lnot Q \lor R, \lnot Q \lor
R\)
From the given Knowledge Base, prove R to be true.

Forward Chaining
The forward chaining algorithm (not to be confused with forward checking!) is really similar in structure to the graph search algorithm. Instead of taking actions like we did in search, we apply Modus Ponens to generate symbols we know to be true. We "find the goal" if we can conclude that the query symbol is true.
Forward chaining has a huge downside: the knowledge base must consist of only definite clauses, and the query is just a positive literal. The nice thing about definite clauses is that they can all be written in the following form: (conjunction of positive literals) \(\Rightarrow\) a positive literal.
The algorithm is as follows:
-
For all clauses in KB and query, count number of symbols in the premise. i.e, if \(P \land Q \Rightarrow L\), count = 2.
-
Add symbols initially known to be true in KB to agenda. Agenda contains symbols known to be true, but not have been used to infer other symbols. The agenda is a queue, similar to the frontier in graph search.
-
Initialize a dictionary \(inferred\), where \(inferred[s]\) is false for all symbols. This is to avoid adding already inferred symbols to the agenda again (think explored set!).
-
While agenda is not empty, pop the symbol \(P\) off the agenda. If \(P\) is the \(query\) symbol, then we know the KB entails the query. Otherwise, if \(inferred[P]\) is false, for all clauses that have \(P\) in the premise, decrease the corresponding count. If the count is 0, by Modus Ponens, we can infer the conclusion since this means all premises are true. Add this new inferred symbol to the agenda and set \(inferred[P]\) to true.
-
Repeat step 4 until
-
we've inferred the query (return true), or
-
we've exhausted the agenda (return false).
-
This algorithm is sound and complete for definite clause knowledge bases, and runs in linear time. Recall that a definite clause is a clause with exactly one positive literal, e.g., \((\lnot A \lor B \lor \lnot C)\). Such clauses are equivalent to an implication sentence, e.g., \(A \land C \Rightarrow B\).
Example:
-
KB: \([A, B, A \land B \Rightarrow L, B \land L \Rightarrow P, P \Rightarrow Q]\).
-
Query: Q
Initially, count = (0, 0, 2, 2, 1) for each sentence in KB as ordered above, and agenda will have A, B.
-
Pop A. Now inferred[A] is True. Count for clause will change as: (0, 0, 1, 2, 1).
-
Pop B. Inferred[B] is True. Count for clauses will become: (0, 0, 0, 1, 1). Notice, count for clause \(A \land B \Rightarrow L\) became 0. Hence, by Modus Ponens we can infer L. Add L to the agenda.
-
Pop L. Inferred[L] is True. Count for clauses will become: (0, 0, 0, 0, 1). Add P to the agenda.
-
Pop P. Inferred[P] is True. Count for clauses: become: (0, 0, 0, 0, 0). Add Q to the agenda.
-
Q = query, so \(KB \vDash Q\)!
Satisfiability
Satisfiability: We say that a sentence \(\alpha\) is satisfiable if there exists at least one model that causes the sentence to evaluate to true.
-
We say that the model satisfies the sentence.
-
As a trivial example, the model \(A = True, B = False\) satisfies the sentence \(A \wedge \neg B\)
-
The sentence \(A \wedge \neg B\) is satisfiable because it is true with model \(A = True, B = False\). There are other models too, but we just need to find one to show satisfiability.
Check Satisfy
It is natural to need a way of checking if a given sentence is satisfied by a particular model.
The PL-True algorithm does exactly this. It takes in a sentence \(\alpha\) along with the model and evaluates as follows:
-
If \(\alpha\) is a literal, then just return the value of that literal from the model.
-
If \(\alpha\) contains a logical operator
-
If the operator is \(\neg\), then recursively call the function with the argument to the negation, and then negate the return value.
-
If the operator is \(\wedge\), recursively call the function on both arguments to the \(\wedge\) and then \(\wedge\) the two results together.
-
This goes on similarly for all of the other logical operators.
-
This great for determining if a given model satifies a sentence. But what if it returns false? To determine if a sentence is satisfiable, you may have to do quite a bit more work!
Boolean Satisfiability Problem
This problem refers to the issue of trying to see if a given sentence is satisfiable or not. A SAT-solver is an algorithm that can do this.
SAT with Model Checking
One simple SAT-solver would be to go through every model (all the combinations of assigning True and False to every symbol), but this has a cost of \(O(2^{n})\) if there are \(n\) symbols and thus may not be feasible for larger problems. Think about how many symbols there are in some of the P3 problems.
One big difference between using model checking for SAT versus model checking for entailment is that with SAT, we return early (with that model as the result) as soon as we find one model that makes the sentence true, whereas with entailment, we can return early (with result False) if we find one model that makes the KB true but not the query.
SAT with Resolution
If you look carefully, you'll see that the bulk of the resolution algorithm to prove entailment is actually is solving the SAT problem. Specifically, the resolution entails algorithm returns true if \(\lnot \text{SAT}(KB \land \lnot query)\). When the resolution algorithm finds an empty clause, then the input \(KB \land \lnot query\) is not satisfiable. If the resolution algorithm runs out of possible clauses to resolve without ever finding the empty clause, then we know the input \(KB \land \lnot query\) is satisfiable, however, we still would have some work to do if we wanted to find a specific model that satisfies the sentence \(KB \land \lnot query\).
DPLL Algorithm
This algorithm is essentially CSP backtracking search, with some heuristics and checks to ensure the minimum amount of work. Note that this algorithm only works for sentences in conjunctive normal form.
There are three things DPLL initially checks for:
-
Early Termination: All clauses are satisfied (\(True\)) or any are unsatisfied (\(False\))
-
In this case DPLL can stop. If all are satisfied then the sentence is satisfiable, and if one is not, then the sentence is not satisfiable, so we return false (the input is in CNF).
-
-
Pure Literals: If all occurrences of any variable have the same sign (so all occurrences are negated or all are not negated), assign a value to it that will make it true
-
This is a way of trying to smartly assign values to variables so that the least number of possible models will be enumerated
-
-
Unit Clauses: If one of the clauses in the sentence is just a single variable, assign the value that will make the clause true.
The full algorithm runs as follows:
-
Check early termination and return true or false as described above.
-
If the algorithm cannot terminate early, find a pure literal then assign that to the correct value and recurse with your new model where that literal is now assigned a value.
-
If there are no pure literals, find a unit clause and repeat the above step.
-
If DPLL cannot do any of the above steps, choose any variable which has not been assigned and recurse twice, one case assigning the literal to \(True\) and the other to \(False\). Return the logical or of these two cases.
Note that in the worst case this will still expand out every possible model, but in some cases the pure literal and unit clause heuristics will save a lot of computation.
Example
Determine whether the sentence below is satisfiable or unsatisfiable using DPLL. Break ties by assigning variables in alphabetical order, starting with True. If satisfiable, what model does the algorithm find?
\((A \lor B \lor \neg E) \land (B \lor \neg C \lor D) \land (\neg A \lor \neg B) \land (\neg A \lor \neg C \lor \neg D) \land E\)
Assign \(True\) to E (unit clause): \((A \lor B) \land (B \lor \neg C \lor D) \land (\neg A \lor \neg B)
\land (\neg A \lor \neg C \lor \neg D)\) Assign \(False\) to C (pure symbol): \((A \lor
B) \land (\neg A \lor \neg B)\)
Assign \(True\) to A (value assignment): \(\neg B\)
Assign \(False\) to B (unit clause or pure symbol): This
sentence is satisfiable and we assign D to be true arbitrarily since it was not assigned during
the algorithm; the model found is \(A: True, B: False, C: False, D:
True, E: False\).
Logical Agents
Fluents
A key first step to doing planning with propositional logic is to figure out how to deal with things changing over time. For example, in Wumpus World, the agent has an arrow that it can use to slay the Wumpus. In this case, we are tempted to change the value of symbols like \(HaveArrow\) and \(WumpusAlive\) from True to False, but this is not how propositional logic works.
Symbols that may change their value over time are called fluents. We deal the passage of time for a fluent by actually creating a different symbol for each possible time point. We can incorporate the time index as part of the symbol name, for example for time points 0-3 we would have symbols: \[HaveArrow[0], HaveArrow[1], HaveArrow[2], HaveArrow[3]\] For planning problems, our actions will have time indices to indicate whether or not we took that action at that time index, for example: \[Shoot[0], Shoot[1], Shoot[2], Shoot[3]\]
Effect Axioms
To encode the logic of how fluents change over time, we could consider using what are called effect axioms. Effect axioms might be our first approach to intuitively write logic cause and effect statements, however, as we'll see, they can often lead to unexpected flaws in our logic.
For example, we may write the following to show the cause and effect of shooting an arrow at time \(t\): \[HaveArrow[t] \land Shoot[t] \Rightarrow \lnot HaveArrow[t+1]\]
But what if the left-hand side of this implication is false, for example, when \(Shoot[t]\) is false? This would still allow for \(\lnot HaveArrow[t+1]\) to be true (remember \(F \Rightarrow T\) is always true). We can tighten this up with a biconditional to say that we lose are arrow if and only if we have and arrow and shoot: \[HaveArrow[t] \land Shoot[t] \Leftrightarrow \lnot HaveArrow[t+1]\]
This is better but starts to break if there is more than one way for the agent to no longer have an arrow. For example, if there were a \(SellArrow[t]\) action in the game, the above logic would prohibit the act of selling an arrow at time \(t\) to result in \(\lnot HaveArrow[t+1]\).
We're going to fix some of these issues with a more rigorous formula for handling fluents called successor state axioms.
Successor State Axioms
Successor-state axioms are axioms outlining a rigorous way of write the logic of how a fluent changes over time. These axioms state that a fluent can be true at time \(t+1\) if and only if:
-
There was some action at time \(t\) that made it true, or
-
It was already true at time \(t\) and no action occurred that would make it false
The general schema for successor state axioms for fluent \(F\) is: \[F[t+1] \Leftrightarrow ActionCausesF[t] \lor (F[t] \land \lnot ActionCausesNotF[t])\]
For example, consider a game with actions \(Shoot\), \(SellArrow\), and \(BuyArrow\) (and max one arrow per agent). The successor state axiom for the fluent \(HaveArrow\) at time \(t+1\) would be: \[\begin{align*} HaveArrow[t+1] \Leftrightarrow & BuyArrow[t] \lor \\ & (HaveArrow[t] \land \lnot (Shoot[t] \lor SellArrow[t])) \end{align*}\]
Planning as Satisfiability
If we have a very efficient SAT-solver, then you can make a plan, which is something that we ask in P3! Note that the environment must be fully observable and deterministic.
If we want to find a plan that takes as few time steps as possible, we can run an algorithm called SATPlan that increases the max allowable time one step at a time until it can find a satisfiable solution in that number of time steps.
-
Let maxT = 1
-
Build a KB with all of the logic for time points 0 to maxT. This includes:
-
The initial state (at time zero)
-
Successor state axioms for any fluents for times points 1 to maxT
-
Any other logic of the environment, for example, exactly one action per time point
-
-
Formulate the goal at time maxT
-
Use the SAT-solver to see if there is a model that satisfies KB and goals.
-
If yes, extract the sequence of actions from that model
-
If no, increment maxT by 1 and try again, repeating steps 2-4
-
Rather than looping for ever, practically, we can set a limit on how high we let maxT get.