0 ![]()
![]() -
- ![]() (y,n)
(y,n) ![]()
![]()
Dann berechnet folgender NC 1-Algorithmus bei Eingabe von natürlichen Zahlen
x ![]() 0, y > 0 den Quotienten
q =
0, y > 0 den Quotienten
q = ![]()
![]()
![]() :
:
AC 0 n : = |x| NC 1 z : =(y,n) NC 1 r : = x - y

x
z
(,,Rest``) AC 0 if r
y then q : =
x
z
+ 1 else q : =
x
z

0 ![]() x - q
x - q ![]() y < y
y < y
Ist nun
0 ![]() r < 2y in obigem Algorithmus gegeben, so ist der Algorithmus korrekt,
denn:
r < 2y in obigem Algorithmus gegeben, so ist der Algorithmus korrekt,
denn:
1. Fall: 0r < y
R = x - q
y = x - y

x
z
= r 2. Fall: y
r < 2y
R = x - q
y = x - y
(
x
z
+ 1) = = x - y

x
z
- y = r - y
0
R < y ,
also in beiden Fällen
0 ![]() R < y . Wir zeigen sogar:
R < y . Wir zeigen sogar:
0 ![]() r < y + 1
r < y + 1
0 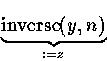 | |||
|
0 |
da n = |x| , d.h.
2n - 1 ![]() x < 2n
x < 2n ![]()
![]() < 1 . Weiter
< 1 . Weiter
|
0 | |||
|
0 | |||
|
y(x |
und wegen
0 ![]() x
x ![]() z -
z - ![]() x
x ![]() z
z![]() < 1 (nach Definition von
< 1 (nach Definition von
![]()
![]()
![]() )
)
0 ![]() x - y
x - y ![]()
![]() x
x ![]() z
z![]() < 1 + y.
< 1 + y.
Also
0 ![]() r < y + 1 .
r < y + 1 .