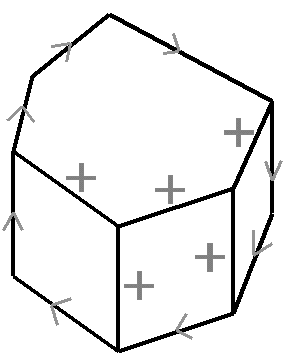
State Space
S0 = <box closed, rope tied, rock smooth>
SGj = <box open, ?, ?>
Also full credit for SG = <box open, rope cut, rock broken>
or reasonable variations.
(we did not talk in this class about most general and most specific representations.)
Operators
BreakRock: <?, ?, rock smooth> ® <?, ?, rock broken>
Also full credit for BreakRock: <?, ?, ?> ® <?, ?, rock broken> because we did not say that you can only break the rock once.
CutRope: <?, rope tied, rock broken> ® <?, rope cut, rock broken>
Also full credit for CutRope: <?, ?, rock broken> ® <?, rope cut, rock broken> because we did not say that you can only cut the rope once.
|
State |
<box closed, rope tied, rock smooth> |
|
Operator |
BreakRock |
|
State |
<box closed, rope tied, rock broken> |
|
Operator |
CutRope |
|
State |
<box closed, rope cut, rock broken> |
Writing out the operators is also OK.
Use broken rock to cut tied rope: rock broken, rope tied -> rope cut.
Open box: rope cut, box closed -> box open.
Search
A*
|
Time |
Priority queue using h heuristic |
|
1 |
(S, f=6) |
|
2 |
(A, f=4), (B, F=7) |
|
3 |
(B, f=7), (C, 10), (D, 8) |
|
4 |
(E, 11), (F, 7), (C, 10), (D, 8) |
|
5 |
(I, 7), (F, 11), (C, 10), (D, 8) |
|
6 |
(H, 7), (F, 11), (C, 10), (D, 8) |
|
7 |
(G, 7), (F, 11), (C, 10), D, 8) |
|
8 |
Term |
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
2. h is admissible because it always underestimates the true cost.
i is not because it overestimates, for example at node H, i=2 but cost=1
Games
Game tree:
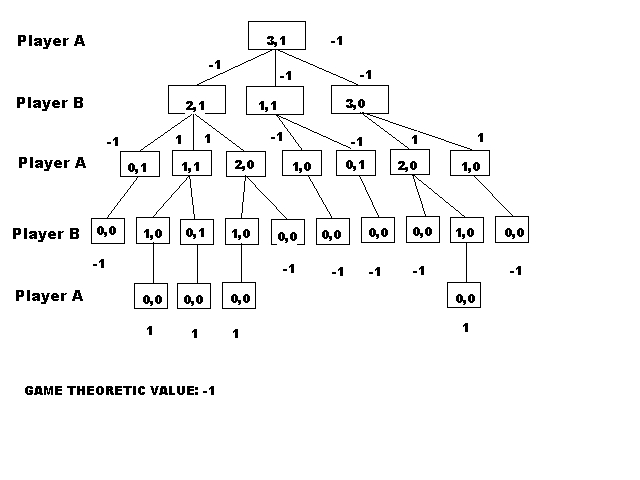
2. Making a suboptimal move against an opponent who may make mistakes might be better because
(One reason is enough for full credit.)
Constraint satisfaction
Waltz algorithm

Job shop scheduling
1. How would you formulate this as a job shop scheduling problem using each document's tasks as variables? ...
Variables are tasks of each job. Let's say D1S is the task of spindling document 1. So variables would be D1F, D1S, D1M, D2F, D2L, D3F, D3S, D3M,D3L. (No need to list them all out, just enough to be clear about the enumeration.)
Values for variables would be assignment to a machine at some time:
cross product of {F,S,M,L} x {1,2,3,4}
Constraints are of two forms, precedence and use constraints:
precedence. {D1F, D1S} = {F1, S2}, {F1, S3}, {F1, S4}, etc.
use. {D1F, D2F, D3F} = {F1, F2, F3}, {F2, F1, F3}, etc.
2. ... using each machine's status as a variable?
Variables are machine assignments at each time:
Let's say F1 is what machine F is doing at time 1.
Variables would be F1, F2, F3, ... , S1, S2, S3, ... , M1, M2, M3, ... , L1, L2, L3, ...
Values for variables are just the component tasks that need to be done:
D1F, D1S, D1M, ..., Idle
Constraints are identical to those in which the tasks are the variables and
jobs are the values.
Logic
Propositional logic
First-order logic

Resolution
Semantic networks
1. Semantic network
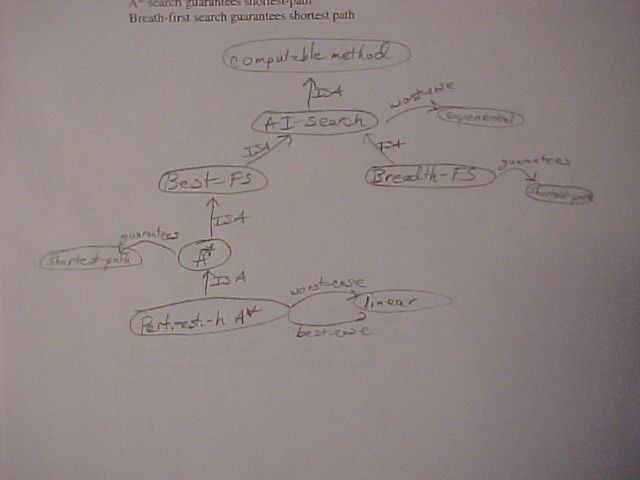
2. Exponential
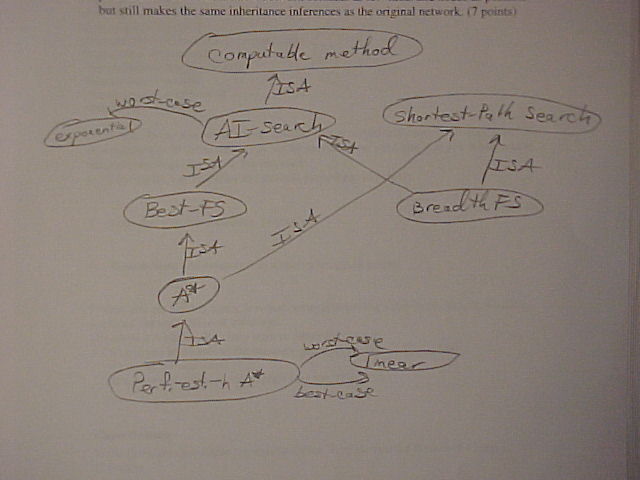
3. Semantic network, redrawn
Natural language processing
Semantic grammars
Case frames
[ head: clean
agent: kim
object: floor
instrument: mop]
2/5 for conceptual dependency structure
Knowledge engineering
Probability
= (30/55 * 55/100) / 35/100 = 30/35 = 6/7
P(Summer|Sad) = (30/100) / (10/100 + 10/100 + 30/100 + 5/100) = 30/55
P(Sad) = 10/100 + 10/100 + 30/100 + 5/100 = 55/100
P(Summer) = 35/100 = 30/100 + 5/100
5.a. Can not compute P(Sad|Cold) because you lack knowledge of conditional independence.
5.b. P(Happy|Warm) = P(Happy ^ Warm) / P(Warm) [by chain rule]
P(Warm) = sum over seasons P(Warm|season) * P(season) [marginalization]
P(Happy ^ Warm) = sum over seasons P(Happy^Warm|season) * P(season) [marginalization]
P(Happy^Warm|season) = P(Happy|season) * P(Warm|Season) [by conditional independence]