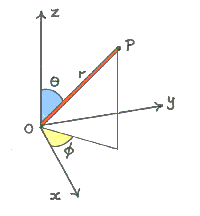
spherical coordinates
The code that we provide allows the user to control the position of the camera by holding the right mouse button and moving the mouse in the horizontal or vertical direction. Use 'z' and 'x' to zoom in/out. Pressing 'e' resets the camera to the original position.
One good way to control the camera is to fix it onto a 3D sphere of some radius R, centered at the origin of the coordinate system. The 3D ball defined by this sphere completely contains the bounding box. Camera always points towards the origin of the coordinate system. The up vector is always (0,0,1).
The camera position on the sphere can be parameterized by two angles Theta and Phi and by the distance from center R. This approach is called the spherical coordinates. The position on a sphere corresponding to Theta, Phi and R is:
x = R * cos(Phi) * sin (Theta); y = R * sin(Phi) * sin (Theta); z = R * cos (Theta);

The angle Phi is the longitude (i.e. traveling around the sphere along a fixed circle, parallel to the equator), and is not constrained. Adding 2*pi to Phi means traveling all around the globe to return to the same position.
Theta is the latitude (declination away from the north pole; for north pole, Theta=0, for equator, Theta=pi/2, for south pole, Theta=pi). Theta must satisfy 0 <= Theta <= pi. Note that in geography, lattitude is usually measured in a different way (declination from the equator). The following relation holds: geographical lattitude = pi / 2 - theta.
Parameter 'R' is the distance from the center of the sphere. Modifying it allows to zoom in/out.
The user controls Phi and Theta by holding the right mouse button and moving the mouse at the same time. Horizontal mouse movement changes Phi, and vertical movement changes Theta. The user can decrease R by pressing 'z' and increase R by pressing 'x'.