Linear Algebra
A common problem in image processing is to try to reconstruct 3-D scenes from photographs taken by multiple cameras. For an fun illustration of how this can be useful, take a look at this mirosoft photosynth video.
As a first step to this we have to solve a simpler problem. Given a picture taken from a camera, we must determine how real-world 3D coordinates get recorded on the picture. In other words, we must determine the pixel locations on the photo where a real-world point $P^w = (X^w, Y^w, Z^w)$ will appear. In this problem we will try to address this issue.
To do this, we must do multiple things. First we must automatically determine where the camera is located (the coordinates of this point). We must determine the camera orientation. Finally we must determine how a real-world point gets modified by perspective when it is recorded in the image. To learn all of this we will use a photograph of a scene where we know the locations $(X,Y,Z)$ coordinates of a couple of points. All of this must be learned from using only astep to this we have to solve a simpler problem. Given a picture taken from a camera, we must determine how real-world 3D coordinates get recorded on the picture. In other words, we must determine the pixel locations on the photo where a real-world point $P^w = (X^w, Y^w, Z^w)$ will appear. In this problem we will try to address this issue.
To do this, we must do multiple things. First we must automatically determine where the camera is located (the coordinates of this point). We must determine the camera orientation. Finally we must determine how a real-world point gets modified by perspective when it is recorded in the image. To learn all of this we will use a photograph of a scene where we know the locations $(X,Y,Z)$ coordinates of a couple of points. All of this must be learned from using only astep to this we have to solve a simpler problem. Given a picture taken from a camera, we must determine how real-world 3D coordinates get recorded on the picture. In other words, we must determine the pixel locations on the photo where a real-world point $P^w = (X^w, Y^w, Z^w)$ will appear. In this problem we will try to address this issue.
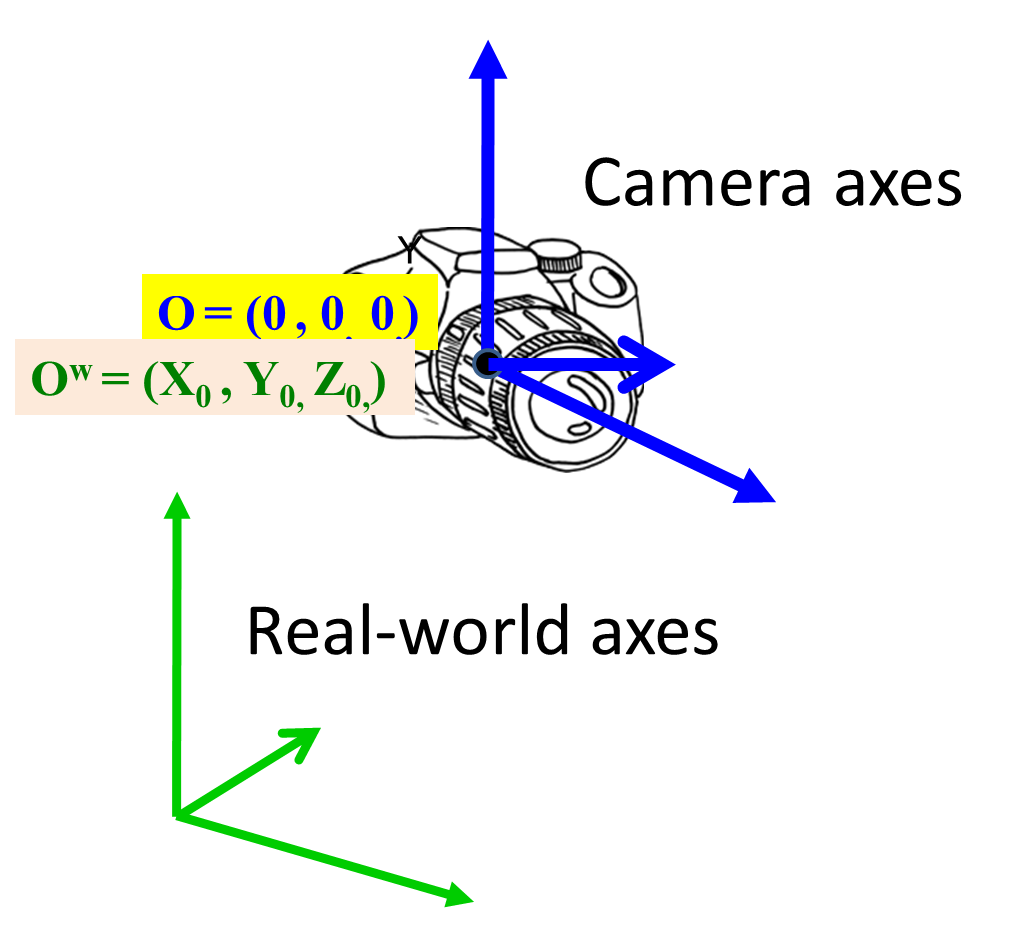
To do this, we must consider an key issue: the camera is a mobile object, and has its own coordinate system. The 3D real world lives by a different, fixed coordinate system. So one part of the problem is to automatically determine the mapping between the real-world coordinates ($(X^w,Y^w,Z^w)$ values measured according to the real-world axes) and the camera-coordinate axes $(X^c, Y^c, Z^c)$ for any point. We also have to consider how a camera records images. Lets consider the latter first.
In all of the notation below we will use the superscript $c$ to represent coordinates obtained in the camera-coordinate system, and the superscript $w$ to represent coordinates in the real-world coordinate system.
Images taken by conventional cameras are in two dimensions, but they are records of a three dimensional world. When a camera takes an picture, the camera is seeing the scene as if it were painted on a 2-dimensional window. The X,Y location of a feature on the image does not give you any indication of the distance of that location from the camera itself. The recorded image is also affected by perspective. To understand this consider what happens when a real-world location $P^c_r = (X^c_r, Y^c_r, Z^c_r)$ is recorded by a camera. Here we're only considering the camera coordinates (as denoted by the superscript $c$).
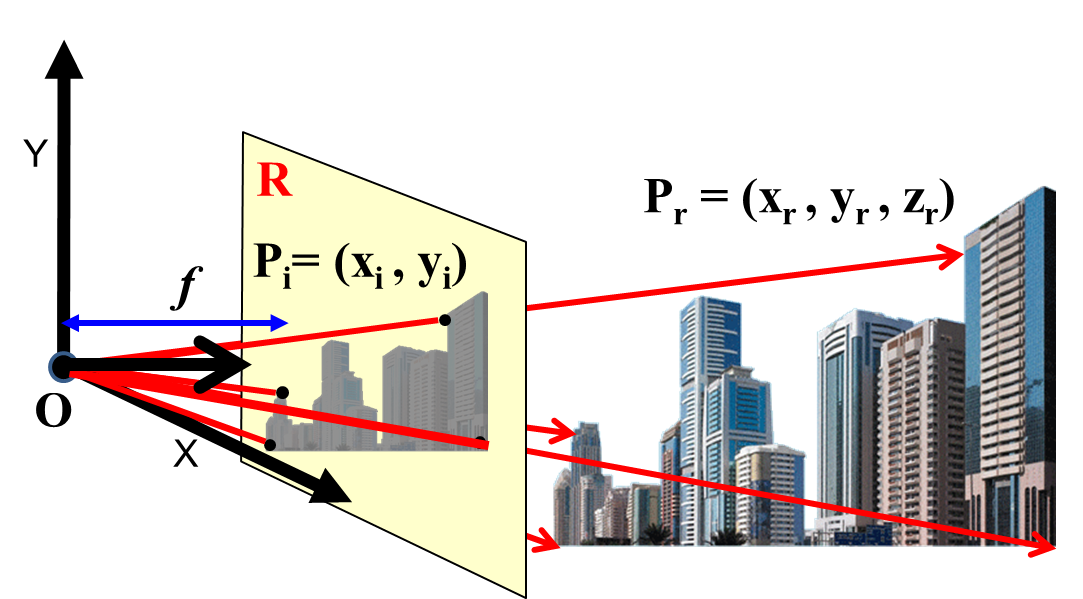
Figure 2 illustrates how an image is recorded by the camera. Rays of light from $P_r$ travel into the “eye” of the camera in a straight line (we are making the simplifying assumption of a pinhole camera here). The point where all the rays converge ($O$ in the picture) is called the “principal point” of the camera. The rectangluar section $R$ through which the ray passes is the “image plane” for the camera. The camera effectively records all pictures as if they were painted on this image plane. The real-world location $P_r$, whose coordinates in the camera-coordinate system are $P^c_r = (X^c_r, Y^c_r, Z^c_r)$ is captured as the image location $P^c_i = (X^c_i, Y^c_i, Z^c_i)$, which is the $X,Y$ location on the image plane where the ray from $P^c_r$ to $O$ intersects it.
N.B: In reality, the actual pixel position recorded is $P_c = (X_c, Y_c)$, where $X_c = s_x X_i + \epsilon_x,~Y_c = s_y, Y_i + \epsilon_y$, where $s_x$ and $s_y$ are scaling factors that scale the image plane down onto to actual pixel locations on the final, captured image. The two scaling factors are not equal, because the image may be differently scaled in the $X$ and $Y$ directions (e.g. the camera may have a different number of pixels per inch in the X and Y directions). $\epsilon_x$ and $\epsilon_y$ are quantization error. For the purpose of this homework we will ignore this aspect and assume that the pixel positions are the $X,Y$ coordinates of the image plane, i.e. $P_c = P_i$.
In practice, the actual pixel positions will depend on how you begin counting pixels (e.g. from the top-left corner, or from the bottom-left corner), and don't represent the real pixel value in the camera coordinate system. We must adjust these so that they are actually given with respect to the principal point of our camera, so that the principal point is the origin of the camera coordinates.
For this homework problem we will make some simplifying assumptions. We will assume that the principal point of the camera is centralized, i.e. it is located exactly behind the center of the image plane. Effectively, we are assuming that the rays converge at a point that on the normal drawn from the centre of the image. We will treat this principal point as the origin, i.e. the $(0,0,0)$ point of the camera coordinate system. This is the point with respect to which all $X,Y,Z$ coordinate values are obtained from the perspective of the camera. All points on the image plane will have the same $Z$ value $Z^c_i$, which is the distance of the image plane from the principal point. We will refer to $Z^c_i$ as $f$, that is, $f = Z^c_i$ is the focal length of the camera.
Having set our notation, let us consider the relation between the camera-system coordinates of $P^c_r$ and its image $P^c_i$. Note that $P^c_r$ and $P^c_i$ are on a straight line. Moreover, since we have set the principal point through which the line passes to be the origin, we get the the following relationships: \[ 1.~~~~~~~~~~~~~~~~~~\frac{X^c_r}{X^c_i} ~~=~~ \frac{Y^c_r}{Y^c_i} ~~=~~ \frac{Z^c_r}{f} \]
or alternately \[\begin{array}{ll} 2.~~~~~~~~~~~~~~~~~~X^c_i = f\frac{X^c_r}{Z^c_r} \\ ~~~~~~~~~~~~~~~~~~~~Y^c_i = f\frac{Y^c_r}{Z^c_r} \end{array}\]
The above equation is entirely in terms of Camera coordinates. Let us now consider the relationship between the camera-coordinate image-plane coodinates, i.e. the pixel locations (after centering the image) of the image of any point in the real world, and its correspoding 3-D real-world coordinates.
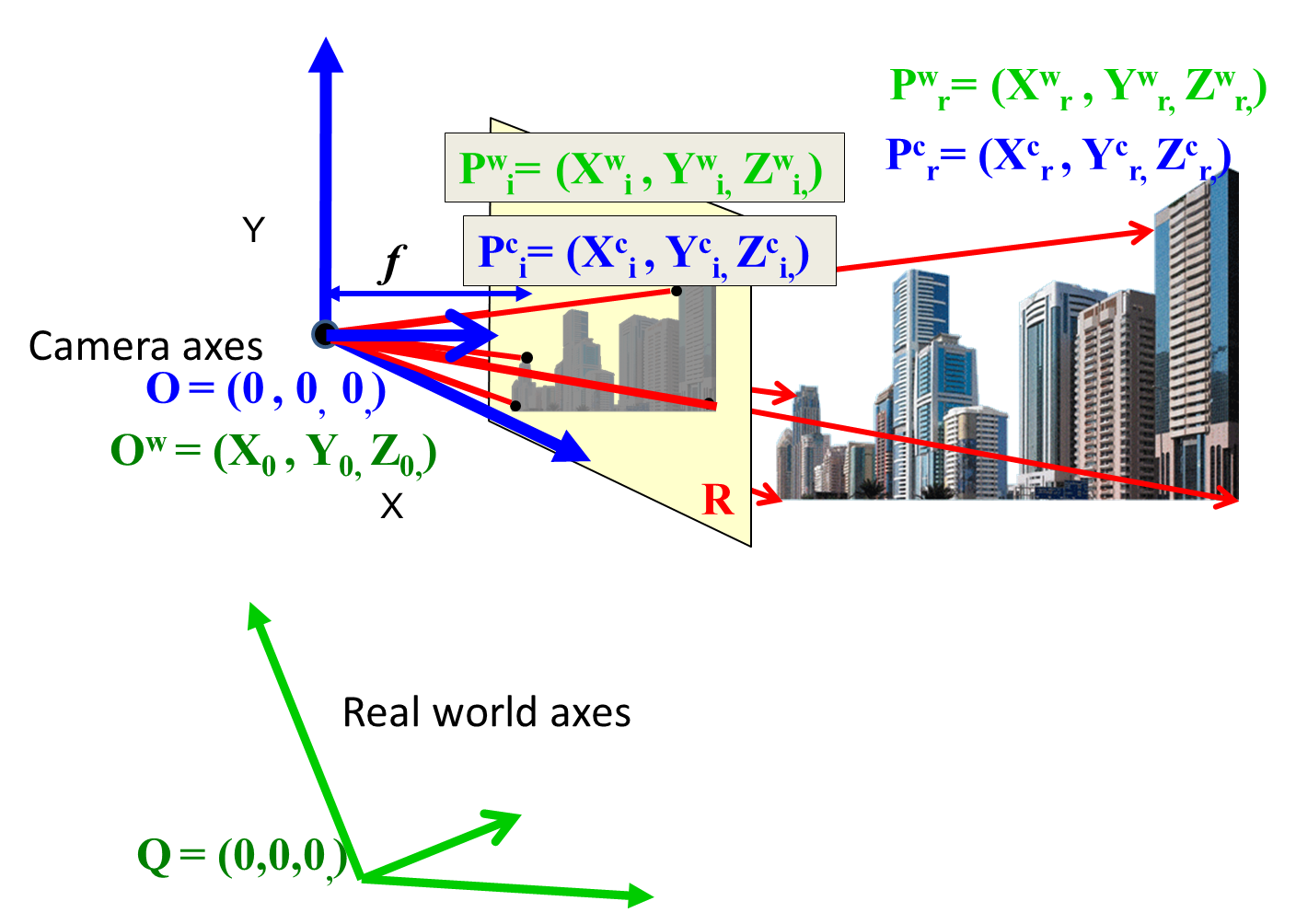
Let $Q$ be the origin of the world coordinates as in the figure below, and let $O = (X^w_0, Y^w_0, Z^w_0)$ be the location of the camera's principal point, i.e. the orgin of the camera coordinates. The relationship between the camera's coordinate system, and the world coordinate system can be defined through a translation and a rotation $R$, accounting for the fact that not only is the camera's origin shifted with respect to the world-coordinate origin, but the cameras axes are also rotated with respect to the axes of the world coordinates. Thus, the relationship between the world-coordinate representation of a point $P^r,~~P^w_r = (X^w_r, Y^w_r, Z^w_r)$, and the camera-coordinate representation of the real-world location $P^c_r = (X^c_r, Y^c_r, Z^c_r)$ of the same point is: \[ 3.~~~~~~~~~~~~~\begin{bmatrix}X^c_r \\ Y^c_r \\ Z^c_r\end{bmatrix} = R\left(\begin{bmatrix}X^w_r \\ Y^w_r \\ Z^w_r\end{bmatrix} - \begin{bmatrix}X^w_0 \\ Y^w_0 \\ Z^w_0\end{bmatrix}\right) \] i.e. it is obtained by shifting the real-world origin to the camera-coordinate origin, and then rotating the axes using $R$ so that the axes of the two coordinate systems are aligned up.
In order to simplify issues, we will write: \[ 4.~~~~~~~~~~~~~\begin{bmatrix}X_0 \\ Y_0 \\ Z_0\end{bmatrix} = R\begin{bmatrix}X^w_0 \\ Y^w_0 \\ Z^w_0\end{bmatrix} \] so that we can rewrite Equation 3. as: \[ 3.~~~~~~~~~~~~~\begin{bmatrix}X^c_r \\ Y^c_r \\ Z^c_r\end{bmatrix} = R\begin{bmatrix}X^w_r \\ Y^w_r \\ Z^w_r\end{bmatrix} - \begin{bmatrix}X_0 \\ Y_0 \\ Z_0\end{bmatrix} \]
From Equation 5 it is clear that in order to establish the complete relationship between the world-coordinates of $P^w_r$ and the camera coordinates $P^r$, we only need to know the world-coordinates of the principal point of the camera, $X_0, Y_0, Z_0$ and the rotation matrix $R$.
N.B: Although the rotation matrix $R$ has 9 components, they are represented by only two variables: the two angles of rotation. We will, however ignore this and assume $R$ has 9 independent components.
In order to establish the complete relationship between the world-coordinates of $P^w_r$ and the camera coordinates $P^r$, we only need to know the world-coordinates of the principal point of the camera, $X_0, Y_0, Z_0$ and the rotation matrix $R$. and the focal length $f$.
However, that by itself is not sufficient. What we record are not real-world camera coordinates $P^c_r$ of any point, but its image plane coordinates $P^c_i$. So we need to find a relationship between the real-world world coordinates $P^w_r$ and the image plane camera coordinates $P^c_i$ for any point. To do so we now also consider the relationship in Equation 1. Combining it with Equation 5, we get the following, where $r_{ij}$ represents the $(i,j)^{rm th}$ entry (at row $i$, column $j$) of matrix $R$: \[ \frac{X^c_i}{Y^c_i} = \frac{r_{11}X^w_r + r_{12}Y^w_r + r_{13}Z^w_r - X_0 } {r_{21}X^w_r + r_{22}Y^w_r + r_{23}Z^w_r -Y_0} \]
or, alternately: \[ 4.~~~~~~~~~~~~~{X^c_i}(r_{21}X^w_r + r_{22}Y^w_r + r_{23}Z^w_r - Y_0) = {Y^c_i}(r_{11}X^w_r + r_{12}Y^w_r + r_{13}Z^w_r - X_0) \]
This implies that knowing $r_{11}, r_{12}, r_{13}, r_{21}, r_{22}, r_{23}, X_0$ and $Y_0$ gives us a relationship that fully specifies how the real-world coordinates of any point $P^w_r$ maps on to its image $P^c_i$ on a photograph taken by the camera.
Problem:
- Given the world-cordinates of a set of $N$ points, $P^w_r(i) = (X^w_r(i), Y^w_r(i), Z^w_r(i)),~~i=1\cdots N$, $N>7$, and their corresponding camera image plane coordinates $P^c_i(i) = (X^c_i(i),Y^c_i(i)),~~i=1\cdots N$, show how $r_{11}\cdots r_{23}$ and $X_0$ can be recovered. Assume $Y_0 = 1$.
- You are given the camera image plane coordinates $P^c_i(i) = (X^c_i(i),Y^c_i(i)),~~i=1\cdots N$ of $N$ points. You are also given the vector difference $P^w_r(i) - P^w_r(j)$ between their corresponding real-world coordinates in the world-coordinate system for $K$ $(i,j)$ pairs, $K>7$. You are not given the absolute coordinates $P^r_i(i)$ for any point, however. Show how $r_{11}\cdots r_{23}$ and $X_0$ can be recovered. Once again assume $Y_0 = 1$. (Hint: Since the world-coordinate origin is not specified, you can choose it to be convenient value, e.g. one of the provided points).
- Download [this] package. It includes four images, a.jpg, abw.jpg, b.jpg and d.jpg. We will work with abw.jpg (which is a black-and-white version of a.jpg). The figure shows a picture that includes a frame with several dots on it. The spacing of the grid is 7cm (i.e along any row or column, the distance between two pixels is 7cm). The included excel file shows the pixel locations of each of nine points from the left, right and bottom panes of the frame. The specific spot on the grid that each of these points refers to is marked on abw.jpg. Using these pixel positions, and the fact that the spacing of the grid is 7cm, find $R$, $X_0, Y_0$ and $Z_0$. To simplify the problem assume the corner of the frame to be the origin of the world coordinates, and the three edges of the frame to be the three axes (so that the three panes are the $X-Y$, $Y-Z$ and $X-Z$ planes, and the grid is parallel to the axes). (Hint: You only need the image to determine which pairs of points are 7cm apart, and along which axis). Important key: Assume that the grids on the three surfaces are each exactly 7cm from the three axes of the box.
Problem 2: A simple face detector
You are given a corpus of facial images [here] from the LFWCrop database. Each image in this corpus is 64 x 64 and grayscale. You must learn a typical (i.e. Eigen) face from them
You are also given four group photographs with multiple faces [here]. You must use the Eigen face you have learnt to detect the faces in these photos
The faces in the group photographs may have different sizes. You must account for these variations
Matlab is strongly recommended but you are free to use other programs if you want.
Some hints on how to read image files into matlab can be found here
You must compute the first Eigen face from this data. To do so, you will have to read all images into a matrix. Here are instructions for building a matrix of images in matlab. You must then compute the first Eigen vector for this matrix. Information on computing Eigen faces from an image matrix can be found here
To detect faces in the image, you must scan the group photo and identify all regions in it that “match” the patterns in Eigen face most. To “Scan” the image to find matches against an $N\times M$ Eigen face, you must match every $N\times M$ region of the photo against the Eigen face.
The “match” between any $N\times M$ region of an image and an Eigen face is given by the normalized dot product between the Eigen face and the region of the image being evaluated. The normalized dot product between an $N\times M$ Eigen face and a corresponding $N\times M$ segment of the image is given by $E\cdot P / |P|$, where $E$ is the vector (unrolled) representation of the Eigen face, and $P$ is the unrolled vector form of the $N\times M$ patch.
A simple matlab loop that scans an image for an Eigen vector is given here
The locations of faces are likely to be where the match score peaks.
Some tricks may be useful to get better results.
- Some of your test images (the group photograph) are in color; your Eigen faces are greyscale. You will have to convert the color photograph to greyscale by taking the mean of the red, green and blue values. The matlab method for doing this is given here.
- You will obtain better Eigen faces if all of the faces in the training data are histogram equalized. The faces in the training data all have somewhat different lighting and contrast. These variations can affect your estimate of the Eigen face. Histogram equalization can be performed in matlab as explained here.
- You will also be able to detect faces better if you histogram-equalize each patch of the group photo before you evaluate its match to the Eigen face.
Scaling and Rotation
The Eigen face is fixed in size and can only be used to detect faces of approximately the same size as the Eigen face itself. On the other hand faces in the group photos are of different sizes -- they get smaller as the subject gets farther away from the camera.
The solution to this is to make many copies of the eigen face and match them all.
In order to make your detection system robust, resize the Eigen faces from 64 pixels to 32x32, 48x48, 96x96, and 128x128 pixels in size. You can use the scaling techniques we discussed in the linear algebra lecture. Matlab also provides some easy tools for scaling images. You can find information on scaling images in matlab here. Once you've scaled your eigen face, you will have a total of five “typical” faces, one at each level of scaling. You must scan the group pictures with all of the five eigen faces. Each of them will give you a “match” score for each position on the image. If you simply locate the peaks in each of them, you may find all the faces. Sometimes multiple peaks will occur at the same position, or within a few pixels of one another. In these cases, you can merge all of these, they probably all represent the same face.
Additional heuristics may also be required (appropriate setting of thresholds, comparison of peak values from different scaling factors, addiitonal scaling etc.). These are for you to investigate.
[More hints]Problem 4: A boosting based face detector
You are given a training corpus of facial images. You must learn the first K Eigen faces from the corpus. Set K = 10 initially but vary it appropriately such that you get the best results. Mean and variance normalize the images before computing Eigenfaces.
You are given a second training set of facial images. Express each image as a linear combination of the Eigen faces. i.e., express each face $F$ as
\[
F \approx w_{F,1}E_1 + w_{F,2}W_2 + w_{F,3}E_3 + \cdots + w_{F,K}E_K
\]
where $E_i$ is the $i$th Eigen face and $w_{F,i}$ is the weight of the $i$th Eigen face, when composing face $F$. $w_{F,i}$ can, of course, be computed as the dot product of $F$ and $E_i$
Represent each face by the set of weights for the Eigen faces, i.e. $F \rightarrow \{w_{F,1}, w_{F,2}, \cdots, w_{F,K}\}$.
You are also given a collection of non-face images in the dataset. Represent each of these images too as linear combinations of the Eigen faces, i.e. express each non-face image $NF$ as
\[
NF \approx w_{NF,1}E_1 + w_{NF,2}E_2 + w_{NF,3}E_3 + \cdots + w_{NF,K}E_K
\]
As before, the weights $w_{NF,i}$ can be computed as dot products. Represent each of the non-face images by the set of weights i.e. $NF \rightarrow \{w_{NF,1}, w_{NF,2}, \cdots, w_{NF,K}\}$.
The set of weights for the Eigen faces are the features representing all the face and non-face images.
From the set of face and non-face images represented by the Eigenface weights, learn an Adaboost classifier to classify faces vs. non-faces.
You are given a fourth set which is a collection of face and non-face images. Use the adaboost classifier to classify these images.
The classifier you have learned will be for the same size of images that were used in the training data (64 x 64). Scale the classifier by scaling the Eigenfaces to other sizes (32 x 32, 48 x 48, 96 x 96, 128x 128).
Train and test data for this problem is here. It is a collection of face and non-face data.Use the data in the "train" subdirectory to train your classifier and classify the data in the "test" subdirectory.
Problem 5
It will generally not be possible to represent a face exactly using a limited number of typical faces; as a result there will be an error between the face $F$ and the approximation in terms of the $K$ Eigenfaces. You can also compute the normalized total error in representation as:
\[
err_F = \frac{1}{N}\parallel F - \sum_i w_{F,i}E_i \parallel^2
\]
where, $\parallel \bullet \parallel^2$ represents the sum of the squares of the error of each pixel, and $N$ represents the number of pixels in the image.
Represent each face by the set of weights for the Eigen faces and the error, i.e. $F \rightarrow \{w_{F,1}, w_{F,2}, \cdots, w_{F,K}, err_F\}$
As in the case of faces, the approximation of the non-face images in terms of Eigenfaces will not be exact and will result in error. You can compute the normalized total error as you did for the face images to obtain $err_{NF}$.
Represent each of the non-face images by the set of weights i.e. $NF \rightarrow \{w_{NF,1}, w_{NF,2}, \cdots, w_{NF,K}, err_{NF}\}$
Learn and build a classifier in the same way you did for problem 3 but including normalized error as a feature. Use this classifier for Problem 4.
Problem 6
Scan the group photographs to detect faces using your adaboost classifier
You can adjust the tradeoff between missing faces and false alarms by comparing the margin $H(x)$ of the Adaboost classifier to a threshold other than 0.
Problem 7
We will add a final problem on the use of independent component analysis for the face recognizer. This will be put up by next week.
Submission Details
The homework is due at the beginning of class on October 31,2013.
What to submit:
- A brief writeup of what you did
- The segments that your detector found to be faces. You may either copy those segments into individual files into a folder, or mark them on the group photograph. Make sure we can understand which part(s) of the image was detected as a face.
- The code for all of this
Put the above in zipfile (tar is fine as well) called "yourandrewid_mlsp_hw2.zip" and email it to the two instructors with MLSP hw2 in the subject line
Solutions may be emailed to James Ding or Varun Gupta, and must be cc-ed to Bhiksha. The message must have the subject line "MLSP assignment 1". It should include a report (1 page or longer) of what you did, and the resulting matrix as well as the synthesized audio.