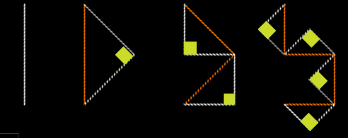Important:

• Due date: Tuesday April 24, 1:30pm, hard copy in class and soft copy e-mailed to the TA in a single e-mail.
• For all questions please BOTH:
  • e-mail the TA a soft-copy of all code, output (including images of plots) and auxiliary scripts tar'ed up in a single file. Please name this file <your_andrew_id>_hw3.tar
  • hand in a hard-copy of all code, output and auxiliary scripts
• Please turn in a typed report -  handwritten material may not be graded, at the grader's discretion.
• All homeworks including this one are to be done INDIVIDUALLY
• For all plots, in addition to a hardcopy printout, please submit an electronic version in postscript, pdf, gif, jpeg, or png format.
• Wherever numerical answers are asked for please provide up to 3 significant digits of accuracy.
• Expected effort for this homework:
  • Q1: 1 hour
  • Q2: 1 hour
  • Q3: 1 hour
  • Q4: 2 hours
  • Q5: 1 hour
  • Q6: 2 hours
  • Q7: 4 hours

Q1: 1-D DFT [10 pts]

Apply DFT to following datasets.

• DS1:  A noisy sine wave.
• DS2:  A different noisy sine wave.
• DS3:  White noise.

For each dataset hand in:

1. [1 pt] The time-plot (value vs time) of the original dataset,
2. [5 pt] The amplitude-frequency ("amplitude spectrum") plot for DFT.
3. [2 pt] What can you say given these plots, e.g. how many strong frequencies are there?
4. [1 pt] Give the sum of squares of the time values.
5. [1 pt] Give the sum of squares of the amplitudes.

Q2: 1-D DWT [10 pts]

Apply DWT using Haar wavelets (code available here) and DFT to this simulated heart beat.

What to hand in:

1. [1 pt] The time-plot of the original dataset,
2. [1 pt] The amplitude-frequency ("amplitude spectrum") plot for DFT.
   1. [1 pt] What can you say given these plots?
3. [2 pt] Plot the scalogram for DWT as a set of histograms (1 per scale). Do the full level decomposition of the signals (you might consider using xwpl (link seems to be broken), so feel free to use anything you wish, like matlab's wavelet toolbox, or see BBoard for alternatives). The histograms should look like the examples starting on slide #100 in in these slides, that is:

     for (scale in 0 to 9){
     	give the 2^scale coefficients as a histogram over time
     }
     also give the smooth coefficient
     

1. [1 pt] What can you say given these plots? Any dominant frequencies? Any spikes?


4. [1 pt] The time plot of the reconstructed version using only  the top 5 DFT coefficients Specifically, pick the 5 best complex numbers of the DFT, that can help you reconstruct the original signal. For the upcoming comparison with DWT, we shall use the concept of  'degrees of freedom' DOF,  counted as follows:
   • every complex number X_f contributes 2 towards the degrees of freedom
   • except for X₀ and X₅₁₂, which by theorem have zero imaginary part
   • Also, when you choose X_f , you can (and should) use X_N-f, for free.
   
   For the top 5 DFT coefficients, the degrees of freedom DOF would be approximately DOF=10 (or a bit less).
1. [1 pt] Give the root mean squared error (RMSE) between this reconstructed version and the original, where RMSE is defined as the square root of the average squared differences between the true values, y, and the reconstructed values, y^:
   
   
5. [1 pt] Give the time plot of the reconstructed version using only  the top DOF  DWT coefficients, where DOF is the degrees of freedom for DFT, defined above. (Notice that for DWT all coefficients are real, and thus each coefficient corresponds to 1 degree of freedom).
1. [1 pt] The root mean squared error (RMSE) between this reconstructed version and the original

Q3: 2D DFT and DWT [10 pts]

1. [2 pt] The 2-d image of the dataset,
2. [2 pt] Draw the 2-d grey-scale image of the reconstructed version using only  the top 3 DFT coefficients as defined in Q2 above. The degrees of freedom (DOF) should be about 6.
1. [2 pt] What is the root mean squared error (RMSE) between this reconstructed version and the original, where RMSE is defined as before, but this time averaging over all pixels (ie, all values of i and j):
   
   
3. [2 pt] Draw the reconstructed version using only  the top DOF DWT coefficients, as defined in Q2 above. The idea, again, is to make it a fair comparison between DFT and DWT. (Use Haar wavelets: DWT each row, then each column).
1. [2 pt] What is the root mean squared error (RMSE) between this reconstructed version and the original?

Q4: Iterated Function Systems [15 pts]

1. Dragon Curve
   
   Write code to generate and plot the following curve for any order n:
   
   The picture below (figure 1) shows four iterations of the dragon curve, from order 0 on the left, to order 3 on the right. The white lines in each image are the current state of the curve. At each iteration, each line segment is split into two line segments by forming a 45-45-90 degree triangle (right angles shown as yellow boxes) with the original line segment (in red) as the hypotenuse. The orientation of this new triangle oscillates, so in the order-2 curve, the lower triangle is formed to the right of the red line, while the upper triangle is formed to the left of the red line.
   
   Order 0       Order 1          Order 2          Order 3
   
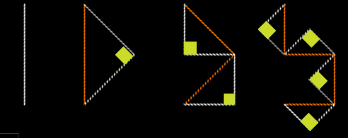
   (Figure 1)
   
   Please submit:
   1. [3 pts] The plot of the curve at order 6 (your code should generate a set of 2-d line segments, which you can plot using your favorite utility, eg, gnuplot, xgraph, etc)
   2. [2 pts] The fractal dimension of the curve in the limit (as n goes to infinity)
   3. [2 pts] Your code
   
    
2. X-shape
   
   Get the IFS code here. Now use it to plot the following X-shape. The picture below (figure 2) shows one iteration of the X-shape. The square is subdivided into nine sub-squares, with the four corners and center square filled, and the rest left empty. For the next iteration, each filled sub-square is further subdivided and filled according to the same pattern.
   
   
   (Figure 2)
   
   Please submit:
   1. [2 pts] The plot of 1,000 points that you generated using Barnsley's IFS algorithm (in the ifs code)
   2. [2 pts] The fractal dimension of the x-shape
   3. [2 pts] The correlation integral (distance vs # pairs) of your 1,000 points (you can use the code here)
   4. [2 pts] Your code (ie, the parts of the IFS code that you modified. Eg, input.parms)
    

Q5: SVD [10 pts]

Consider the following Document by Term matrix: DocTerm

The file is in csv (comma-separated-values) format with windows end of line termination. In this file each row denotes a document, and the columns denote terms. An entry (i,j) denotes the number of occurrences of the j^th term in the i^th document. Based on their occurrence in the documents, the terms can be clustered as belonging to a particular Topic. Run SVD on the dataset to determine the number of topics present. You can use any standard software (e.g., Matlab).

1. [3 pts] The SVD components (the U, lambda, V matrices, specifying which is which).
2. [1 pts] Your estimate of the number of topics for the DocTerm dataset.
3. [6 pts] For every topic, give a sorted list of documents (specified by row-id) that participate in this topic, along with their weight in the topic. For example:

   Topic A:
   --------
   doc 1, weight .9
   doc 2, weight .2
   doc 3, weight .8
   Topic B:
   ------
   doc 1, weight .1
   doc 2, weight .8
   doc 3, weight .2
   

Q6: 3-D SVD [15 pts]

1. Points are sampled from a three dimensional (N=3) spherical (Sigma is now the 3x3 identity matrix) Gaussian centered at the origin (mu is now the vector: <0, 0, 0>).
   1. The first coordinate of the sampled point is multiplied by a scalar a
   2. The second coordinate of the sampled point is multiplied by a scalar b
   3. The third coordinate of the sampled point is multiplied by a scalar c
2. These warped points are all finally rotated and translated by some unknown affine transformation (which is the same for all points).

Q7: Regression and Recursive Least Squares [30 pts]

• Language: You may choose among C/C++, perl, python, Java, R, Matlab. However, your algorithm must be incremental, processing one row of data at a time.
• Input format:  n+1 numbers per line, blank separated; the last column is the dependent variable

  <x1> <x2> ... <y>
  

Output format: n regression coefficients, w₁ ... w_n, so that
<last-column> ~ w₁ * <column-1> + ... w_n * <column-n>
For example, you could use this python code which (a) needs "Numerical Python", and (b) has no forgetting factor.
You can "tar xvf" and then "make" it.
Note: The code is provided to mainly show you the expected formats of the input and output. Make sure you test it thoroughly, or rewrite it from scratch. If you choose to rewrite it make sure that your RLS algorithm is incremental, processing one line at a time.

<calories consumed> <hours of exercise performed> <cholesterol>

y = w1*x1 + w2*x2 + noise

What to hand in:

1. Plot both the time-series of how w1(t) and w2(t) change over time, and the 2-d scatter plot of <w1(t), w2(t)> over time t, as estimated by:
1. [4 pts] RLS with no forgetting (ie, lambda = 1)
2. [4 pts] RLS with the forgetting factor lambda = 0.95
3. [4 pts] OLS with no forgetting (ie, lambda = 1)
4. [4 pts] OLS with the forgetting factor lambda = 0.95
2. [2 pts] Based on these plots, when (which week) did the patient begin taking her medication?
3. [2 pts] Give the running times (wall clock) of each of the four experiments, and the specifications of the machine you ran it on (eg, win xp, 256 mb ram, intel dual core 3 ghz)
4. [10 pts] Submit your code for both RLS and OLS