The visual tracking of a point feature in the neighborhood of the rover allows the rover to use that point as a landmark. The projection of the scene representing the world onto the image plane of the camera on board the rover reduces the information available to 2 dimensions, resulting in a loss of information about the range to the feature. However, under the assumption that the point does not move relative to the world coordinate frame (the surface of some other planet, for instance) we can estimate where the point is located given multiple measurements of the azimuth to the feature from several locations as well as where the observations were actually made. Unfortunately, there is no good source of information for the rover to know where it is taking the measurements--indeed, that is the point of this work. However, given some uncertain means for estimating the positions from which the rover makes observations, such as dead reckoning, and some means of combining multiple noisy measurements, such as a Kalman filter, we can eventually find estimates of landmark positions which will be useful for navigation.

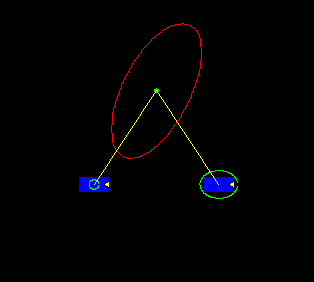
This figure shows two rover positions, each with an uncertainty ellipse represented by the green ellipse around the rover center. The ellipse in this case represents the 99% confidence interval on the robot location. Note that the uncertainty ellipse on the rightmost position is larger, which is reasonable for a rover which is accumulating errors in its position estimate through dead reckoning. The observations (yellow rays) of the landmark azimuth from each position are combined to yield a position for the observed point feature. The uncertainties are combined to give an estimate of the uncertainty in the position measure for the feature point. The 99% confidence interval on the point feature location is shown by the red ellipse.
Given a pair of rover positions and a pair of observations of target azimuth from those positions, we have enough information to compute the position of the point feature explicitly and estimate an uncertainty in the resulting measure. If we can gather multiple pairs, we can combine the measurements resulting from each pair using a Kalman filter to update the estimate as well as the uncertainty. However, we can do better...
Assume that the rover has an estimate of the position of a point feature with uncertainty as above. If a new observation is made from a new location, and we again have the uncertainty on the location and azimuth measurements, we can combine the old estimate and the new measurement using an Extended Kalman Filter (EKF).
The only thing required to get started is an initial estimate of the position of the feature and an initial uncertainty. We can initialize our estimate of the position with an arbitrary (x,y) point, say (0,0), and infinite uncertainty, allowing the point to be anywhere in the plane. After the first measurement, the EKF will disregard the initial estimate and yield a result which is consistent with the new measurement only. Since we have no range information, this will yield an uncertainty region which is unconstrained along one axis (the azimuth to the target) and constrained along another (the axis perpendicular to the observation). After the second measurement, the uncertainty region will be exactly the same as would be given by the measurement pair method above.
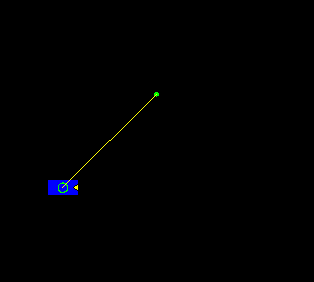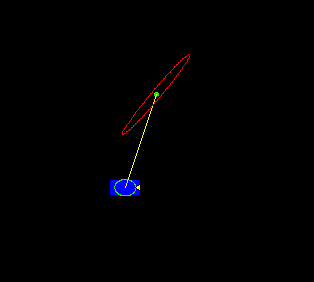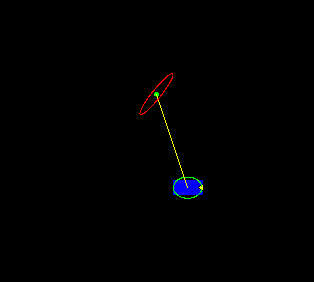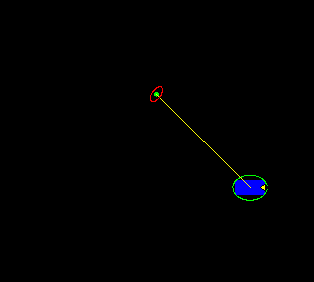
The animation above shows the rover recursively building an estimate of the landmark position one measurement at a time. In the first frame, the uncertainty ellipse around the landmark position (in red) is essentially infinite, which is why the ellipse does not appear in the image window. As the rover traverses from left to right, the uncertainty ellipse representing the rover's estimate of its own position (in green) increases in size due to the accumulation of error in dead reckoning. Even though the rover is accumulating error in its own position, the estimate of the position of the landmark is improving monotonically.
Future work in estimating the position of observed landmarks includes:
|
This page is maintained by Matthew Deans, a
robograd
in the Carnegie Mellon University School of Computer Science.
Comments? Questions? Mail me at deano@ri.cmu.edu Last Modified November 18th, 1997 |