Tracking using the SLOG operator

The Sign of Laplacian of Gaussian operator has proven to be useful in visual tracking of natural terrain features. Essentially, the SLOG is very similar to the approach of convolving an image with a Laplacian of Gaussian kernel and finding zero crossings to extract edges, except that in SLOG computation, the sign is recorded rather than the existence of a sign change. The result is a segmentation of regions, rather than extraction of lines. In practice, the SLOG is actually calculated using a difference of Gaussians, not a Laplacian of Gaussian. Although the two are not numerically identical, they possess similar properties, but the difference of Gaussians allows kernel separation for faster computation.

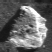
The image above shows a section of an image taken in the sandbox at NASA Ames Research Center in Moffet Field CA using a CCD camera mounted on the Marsokhod rover. This image shows a region of the full image which will be used as an area of interest (AOI) for correlation search. The AOI contains a terrain feature, in this case a lightly colored rock, which is the same rock previously stored as the feature template.

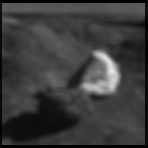
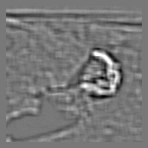
The next two images show low pass filtered versions of the AOI, where the image on the left was filtered using a higher cutoff frequency.

On the left above is the difference image, which is a band-pass filtered version of the original image where the passband is given by the cutoff frequencies of the two low pass filters applied to the original image. In the middle, the difference image is binarized by thresholding the image at zero, so that all pixels with a negative or zero value become zero and all pixels with a positive value become one. The resulting image is packed into 32 bit words, so that an entire row of the search space fits into four words in the computer's memory. On the right, the 32x32 pixel template has been filtered in the same way and stored in 32 bit words.

The correlation can now be done in binary using the XNOR operation and single bit shifts to match the template against the search region. For every pixel where the template matches the area of interest for a given translation of the template, the XNOR yields a one, and where the template and AOI do not match, XNOR yields zero. By finding the weight of the result (the number of pixels of value one) we have a measure of match between the template and the area of interest for every point in the search space. The SLOG takes advantage of binary operations to run at much faster speeds than SSD and normalized correlation.

The above image shows the correlation surface for the area of interest above. The white pixel on the right side of the correlation surface corresponds to the highest weighted result of the XNOR operation, which represents the best match. The figure below shows the point on the original image plane corresponding to that correlation peak.

Conclusion

Sevaral template matching techniques have been studied in the context of tracking natural terrain features for visual servoing and landmark based navigation, including Sum of Squared Difference (SSD), normalized correlation, and Sign of Laplacian of Gaussian (SLOG). Normalized correlation and SSD matching have advantages over SLOG in that the correlation surface reveals some information about the quality of the match in both the magnitude of the peak of the correlation surface, and the curvature of the surface in the neighborhood of the peak. However, these approaches are computationally expensive when compared to the binary operations of SLOG correlation, which has been run at nearly six times the speed of the other approaches. This means that by using SLOG correlation, the tracking can either take advantage of measurements separated by one sixth the time difference as compared to the other methods, which means that feature points don't move as much between frames, or make can measurements at the same frame rate but search six times the area of the image plane for correlations, which covers more candidate match points and allows more exhaustive search between frames. Either way, the tracking is more robust to errors in predictions about where the feature will appear on the image plane in a newly acquired image. The result is more robust visual tracking.

Also, the band-pass filtering inherent in the SLOG computation makes the approach more robust to both high frequency noise and low frequency DC offsets (brightness changes).

Acknowledgements

I would like to thank Dave Wettergreen, Hans Thomas, and Maria Bualat for their help this past summer in working with SLOG correlation and visual tracking and servoing in the Intelligent Mechanisms Group at NASA Ames Reserarch Center. In spite of ongoing excitement over Nomad's Atacama Desert Trek and the Mards Pathfinder landing, they found time to support and advise me in my work there. The field tests of the above tracking method in August using the Marsokhod rover proved invaluable, as did the entire experience.

I'd also like to thank the rest of the IMG for their help during my stay, especially Dan Christian for pointing out obvious solutions to hardware problems which I kept overlooking, Kurt Schwehr and Paul Henning for advice on a few software bugs, Eric Zbinden for his usually insightful comments, and Mike Sims for his continuing support for this effort.

This page is maintained by Matthew Deans, a robograd in the Carnegie Mellon University School of Computer Science.
Comments? Questions? Mail me at deano@ri.cmu.edu
Last Modified September 10th, 1997