Visual Tracking

Current Work:

We are currently working on the problem of robustly tracking a natural feature in a stream of images. See the old page for a quick overview of the approach.

Template Update:

The current task is to determine how to update the template during matching and searching. The problem is that as the camera moves relative to a feature which is being tracked, the appearance of the feature changes. In order to robustly track the feature, then, we will need to update our internal representation of the feature.

Original Instance

This is not a good solution because we know that the appearance of the feature will change. The template ends up being matched against an erroneous part of the image and is lost. Figure 1 shows tracking using the original instance of the feature.

NOTE: In Figure 1, (and the other animated figures in this document) the red box bounds the space over which the search is executed for the best match M(i) to the template T(i). The yellow box bounds M(i). If Figure 1 appears to stop moving, you can either reload this page or open the image file itself.

Newest Match

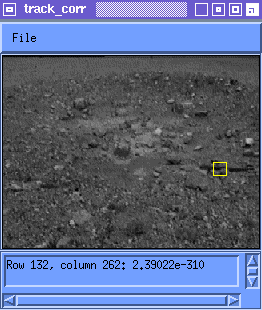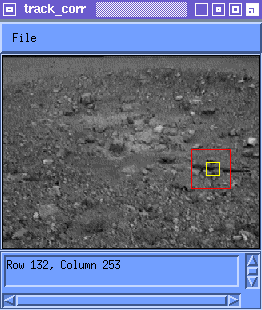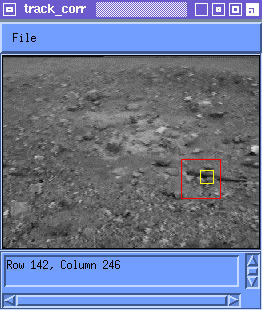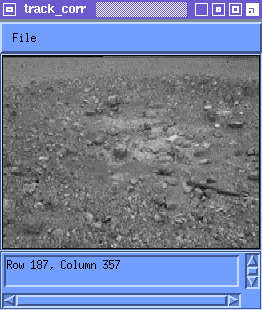
where M(i) is the best match to T(i) in Frame i. Figure 2 shows tracking using the latest instance of the feature.

This approach works better than the first, but problems arise due to the subpixel shifts of the feature on the image plane. If the feature is acquired from location (x,y) in Frame i, then in Frame i+1 the feature may appear at (x+u,y+v) where u and v are not necessarily integers. The subpixel inaccuracies accumulate over the series of several frames and turn into drifts of more than a few pixels. There is no reason for the fractional part of u and v to be correlated over frames and matching takes care of the integer parts of u and v, so in general, the effect is that the feature takes a random walk through template space. It would be advantageous to keep some information about what the feature used to look like, rather than throwing it away.

Affine Transformation

The template used in the i+1 frame should be as similar as possible to the best match in Frame i, M(i). Therefore, we want A(i) such that

The affine transformation is assumed to be small from frame to frame and is built iteratively, updated after the matching step in each frame, that is

where E(i) is the error between the current affine mapping and the estimated correct affine mapping which produces M(i). This works quite well for 2-D objects and orthographic projection (as in tracking the ground from an autonomous helicopter), but for nearby, 3-D, irregularly shaped objects and a perspective camera (as we have here) the approach does not work well. A natural feature does not in general look like an affine transformation of the original appearance of that feature.

Temporal Filtering

This way, the update can take into account any distortions, including affine transformation. For a=1, the update rule is equivalent to

which was the first approach discussed. For a=0, the update rule is equivalent to

which was the second approach discussed. Empirically, for values of a near unity, but less (say a=0.9), tracking can work quite well. The incorporation of new information allows the distortions of the feature to be accounted for. The retention of old information reduces the effects of drift. Figure 3 shows tracking using the weighted average update rule with a=0.9.

Evaluating Performance:

Correlation:
One figure of merit is the value of the normalized correlation between the template and the best match,

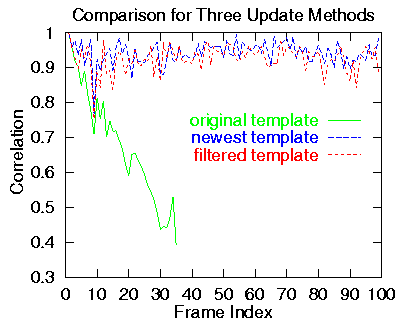
where T(i) and M(i) are T(i) and M(i), respectively, after normalizing. Figure 4 shows the normalized correlation between the template and the best match for 100 frames using the Original Template rule (green), Newest Match rule (blue), and the Filtered Template rule (red). The Original Template curve stops at Frame 35 because the feature was lost around Frame 31 and by Frame 35, the search space was off of the image plane. The Newest Match correlation is slightly higher than the Filtered Template correlation on average, which is to be expected.

This experiment was repeated for several features in this video sequence and other sequences and similar results were obtained.

Feature Retention:
As Figure 1 shows, the feature is only successfully tracked for about 31 frames before the template is matched against some region of the search space other than the actual original feature we wanted. This is not an effect of drift, the feature is tracked reliably for 31 frames and then suddenly jumps far away from the original feature. This number of frames is no magic number, either. Depending on the feature and camera motion, it may be possible to track a feature for a very long time without updating the template: consider tracking a perfect sphere, with no occlusions, where the distance between the camera and sphere does not change. It will always appear the same! Then again, it may be possible to lose the feature much faster, too. Consider tracking a very irregularly shaped 3-D object from a quickly moving train.

For the Newest Match rule amd for the Temporal Filter rule, the feature is retained well throughout the sequence.

Drift:
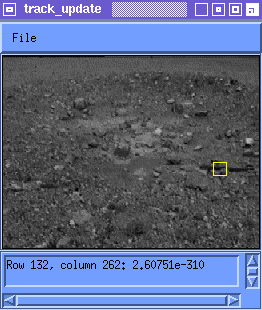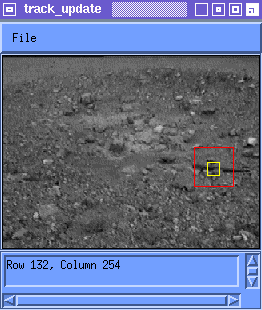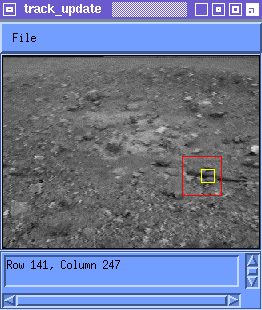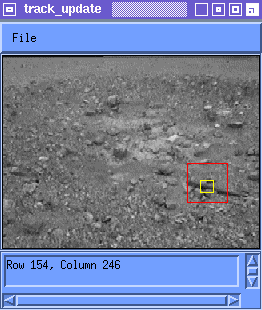
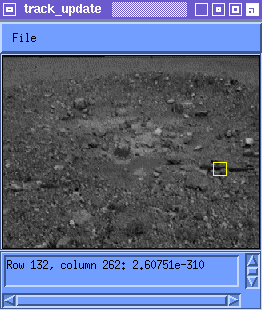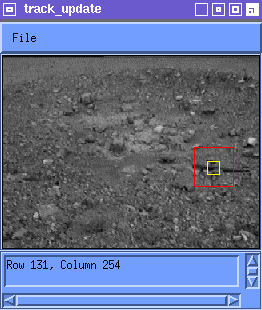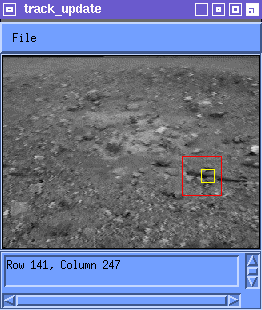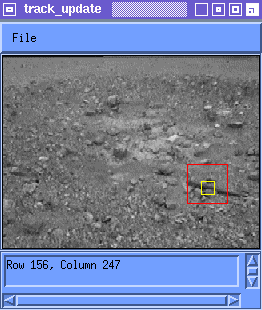
Figure 5 shows the match in Frame 99 which is identified as being the feature originally acquired in Frame 0 for two update rules. The best match for the Temporal Filter update appears much closer to the original feature than for the Newest Match update rule.

Notice in Figure 5 that the original feature selected contains the upper left corner of a rock and a section of a piece of wood adjacent to it. The Temporal Filter rule yields a best match M(99) which contains the same corner of the same rock and the adjacent part of the piece of wood. The Newest Match rule yields an accumulated drift of about 10 pixels away from that original feature. This experiment was repeated for several features in this sequence and others and yielded similar results.

Conclusions

The temporal averaging chosen here, using a fixed coefficient filter, has many advantages to methods proposed other than the peformance as measured by the three figures of merit discussed here.

• The temporal filtering can incorporate arbitrary feature distortions into the tracking step, not just effects seen for a 2-D object under orthographic projection.
• The filter coefficients can be optimized to yield a frequency response which is appropriate for the task. That is, if the feature should not change quickly, we can keep a large value of a which will cause T(i) to have very small high frequency components. This would make the update less sensitive to noise, occlusions, etc.
• The computational complexity of the weighted averaging step is trivial compared to the implementation of the affine mapping update.

Future Plans:

1. Determine useful figures of merit for tracking, other than the correlation, retention, and drift.
2. Come up with a more effective way of measuring figures of merit, whether they are those discussed here (correlation, retention, drift) or new ones.
3. Determine a way to find the best value of a to use for tracking. Hopefully this will be a more-or-less straightforward evaluation of figures of merit for different values of a.
4. Derive position estimates from tracking measurements. Use the position estimates derived for tracked features to produce an estimate of the rover position.

• Original Template method (Figure 1)
• Newest Match method (Figure 2)
• Temporal Filter method (Figure 3)

This page is maintained by Matthew Deans, a robograd in the Carnegie Mellon University School of Computer Science. Comments? Questions? Mail me at deano@ri.cmu.edu Last Modified March 5, 1997