


Example of the duckie model. The first spin image was generated using vertices only. The second one was generated using interpolated points between the vertices. For surfaces in which the vertices are dense and evenly distributed, the two methods should produce nearly identical spin images.






Comparison of spin images at different resolutions. Two versions of the duckie model were created: a low-resolution one (left) and a high-resolution one (right). The top row of spin images shows the same point on both models using vertices only. Notice that the two images are substantially different. The low-resolution version is particularly blocky due to the low number of points falling into each bin in the spin image. The bottom row shows spin images for the same point generated using interpolated points. The low-resolution image is much smoother and more similar to the high-resolution version.



Real terrain data. This is an example of real terrain data gathered using a scanning laser rangefinder. The top and front views of a small valley are shown at left and in the center respectively. The right picture illustrates the large variation in resolution of the surface mesh due to the perspective from which ground-based range data is collected.


Example of planar area. The green circle shows the area of the surface that is used to calculate a spin image. The closeup at right shows the actual interpolated points that were used.
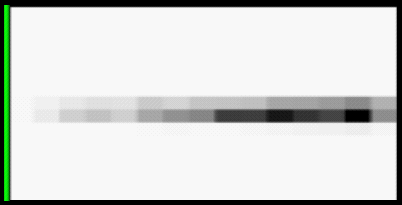
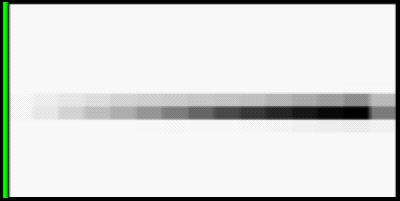
Spin image from planar area. Using only vertices (left), the spin image for a plane is very noisy, going from dark to light to dark with increasing distance from the basis point. Ideally, the spin image of a plane would steadily increase in darkness with increasing distance from the basis. The spin image generated using interpolated points (right) closely approaches this ideal.



Non-planar regions. For non-planar regions, the interpolation method (right) produces a spin image that is substantially the same as the vertex method (center).
| Last modified May 5, 1998 Daniel Huber ( dhuber@cs.cmu.edu) |