2596 - Acceptable Strings

	2596 - Acceptable Strings North America - North Central - 2002/2003

A deterministic finite automaton has a finite set of states, with directed edges leading from one state to another. Each edge is labeled with a symbol. In this problem, we are only concerned about automata (the plural of automaton) that use the binary digits 0 and 1 as symbols. Each edge is thus labeled with 0 or 1. One state is identified as the start state, and one or more states are identified as final states.

A finite automaton is usually represented by a graph. For example, consider the finite automaton represented by the graph shown below; the states are shown as circles, and are named 1 and 2 for ease of identification. In this automaton, state 1 is the start state, and state 2 is the final state.

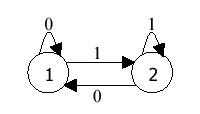
$\epsfbox{p2596.eps}$

Each automaton in this problem accepts or rejects a string as follows. Beginning in the start state, for each symbol (0 or 1) in the input string (working from left to right in sequence), the automaton follows the one edge labeled with the input symbol from the current state to the next state. After making the transition associated with the last symbol in the input string, if the automaton is in a final state, then the input is accepted. Otherwise (that is, if the automaton is not in a final state), the input is rejected.

For the string 0101 and the automaton shown above, we start in state 1 (the start state). Since the first input symbol is 0, the edge labeled 0 from state 1 back to state 1 is followed, leaving us in state 1. The next input symbol, 1, causes a transition to state 2. The next symbol, 0, moves us back to state 1. The last input symbol, 1, causes the last transition, from state 1 to state 2. Since state 2 is a final state, the automaton accepts the string 0101. Note that the string 010 would have been rejected, since the automaton would have been in state 1 (which is not a final state) at the end of the input. This automaton happens to accept all binary strings that end with 1.

In this problem you will be given one or more automata and an integer N . For each of these, you are to find the number of binary strings having each length less than or equal to N that are accepted by the automaton. For example, for N = 3 with the automaton above, the output would specify 0 strings of length 0 (since state 1 is not a final state), 1 string of length 1 (1), 2 strings of length 2 (01 and 11), and 4 strings of length 3 (001, 011, 101, and 111).

Input

There will be multiple input cases. For each case the input begins with three integers N , S , and F . N (no larger than 10) specifies the maximum length of the strings that are sought. S (no larger than 100) specifies the number of states in the automaton. F (no larger than 10) specifies the number of final states. Following these three integers are S pairs of integers. Each pair specifies the labels on the edges from the states, in order, starting with state 1. The first integer in each pair specifies the state to which the edge labeled 0 connects; the second integer specifies the state to which the edge labeled 1 connects. Finally, the last F integers identify the final states. State 1 will always be the start state. The input for the last case is followed by three zeroes.

Output

For each case, display the case number (they are numbered sequentially, and start with 1). Then display the number of strings of each length (from 0 to N ) accepted by the automaton, using a separate line for each length. The output must be identical in format to that shown in the examples below.

Sample Input

Sample Output

Case 1:
    Length = 0, 0 strings accepted.
    Length = 1, 0 strings accepted.
    Length = 2, 0 strings accepted.
    Length = 3, 0 strings accepted.
Case 2:
    Length = 0, 0 strings accepted.
    Length = 1, 1 string accepted.
    Length = 2, 2 strings accepted.
    Length = 3, 4 strings accepted.
Case 3:
    Length = 0, 0 strings accepted.
    Length = 1, 0 strings accepted.
    Length = 2, 0 strings accepted.
    Length = 3, 0 strings accepted.
    Length = 4, 0 strings accepted.
    Length = 5, 32 strings accepted.
    Length = 6, 0 strings accepted.
    Length = 7, 0 strings accepted.
    Length = 8, 0 strings accepted.
    Length = 9, 0 strings accepted.
    Length = 10, 0 strings accepted.
North Central 2002-2003