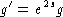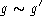given a metric g, you can define another metric . , are called conformally equivalent. This is an equivalense relation. . There are conformal equivalence of metrics on a manifold. This is called the conformal structure. The equivalence classes from a group called .

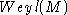Example: all entire functions are conformally equivalent.

source psfile jl@crush.caltech.edu index