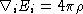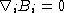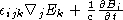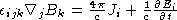, 
, 
, 
. Introduce a vector potential:
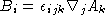, and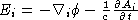 
. The A and 
have some gauge freedom.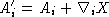 
preserves the 
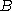. In
order to preserve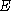 
, you must set 
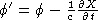. The lorentz condition is a specification
of the gauge: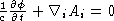 
. This is a lorentz covariant gauge. Define 
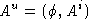, then
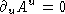is a lorentz scalar. Define 
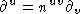, then you get 
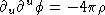and 
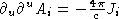. Define 
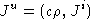then
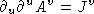in the lorentz gauge. Note that 
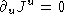. This is conservation of charge.
In integral form this is: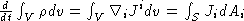 
. Then 
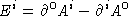and 
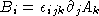. Define 
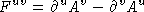as the field strength
tensor.