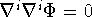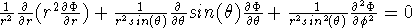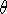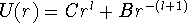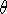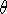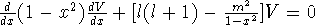In spherical coordinates, you get as . This seperates via with and associated legendre polynomials in . The radial equation is . The equation transforms via x=cos( ) to . l has to be integer to get a convergent power series. This solution is legendre polynomials for m=0 and associated legendre polynomials for other m. The solution is typically written in terms of the spherical harmonics as: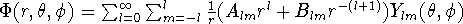
source psfile jl@crush.caltech.edu index spherical_coordinate_green_function laplacian