 |
 |
 |
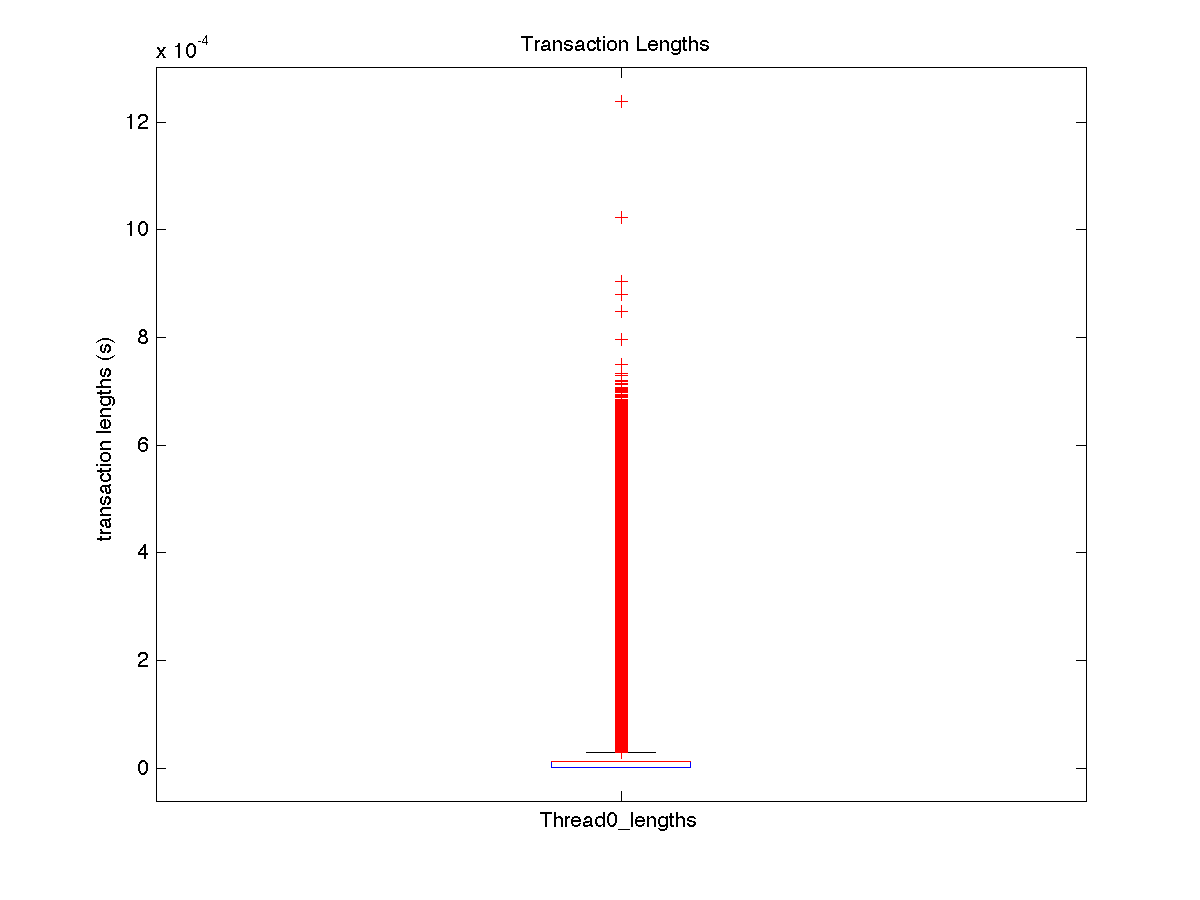
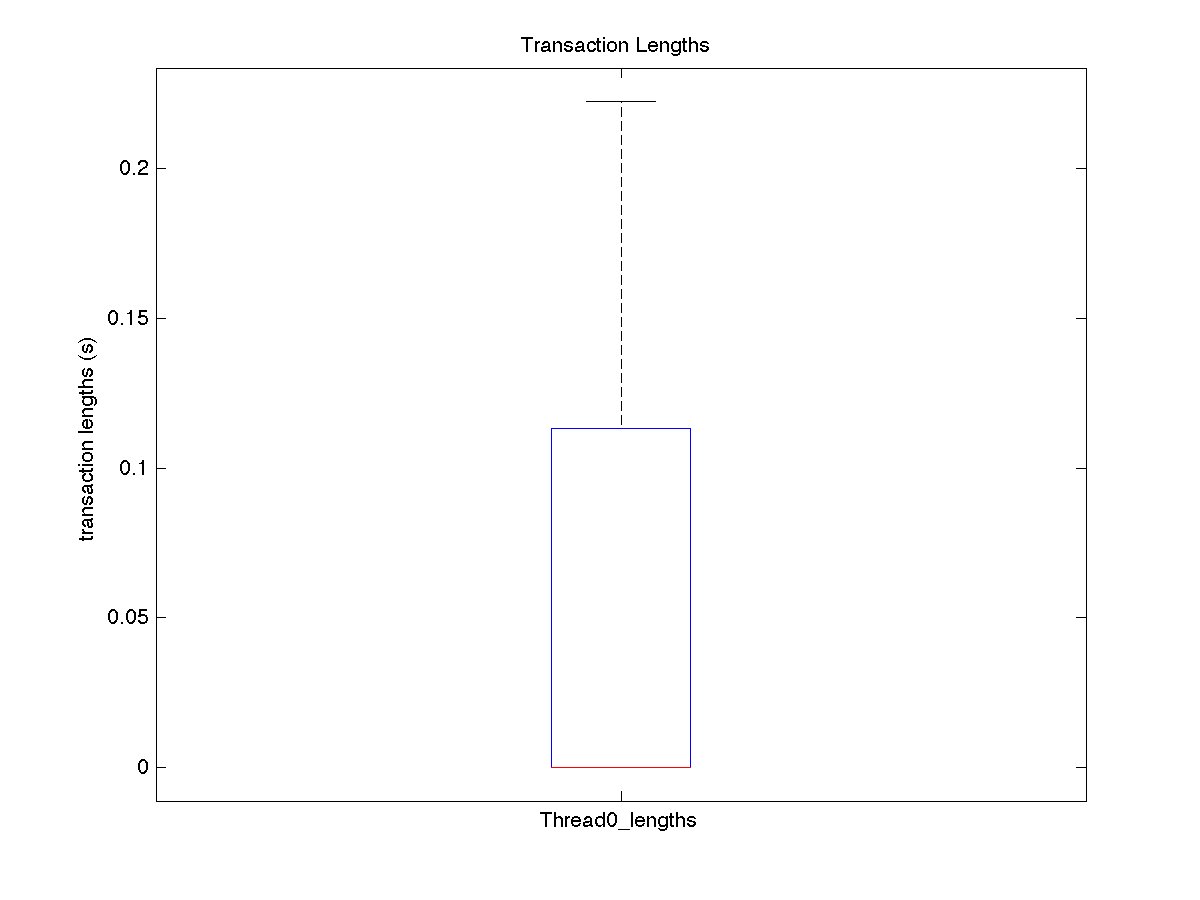
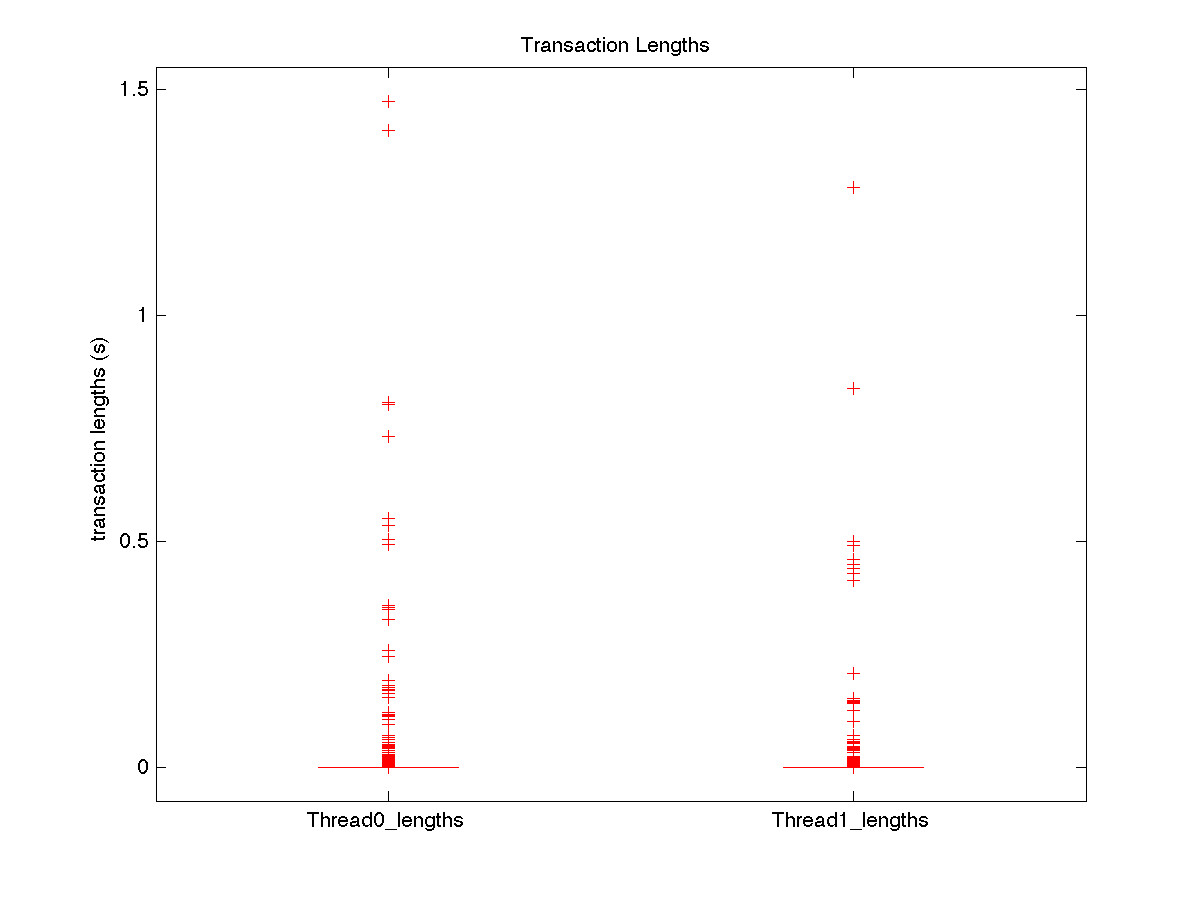
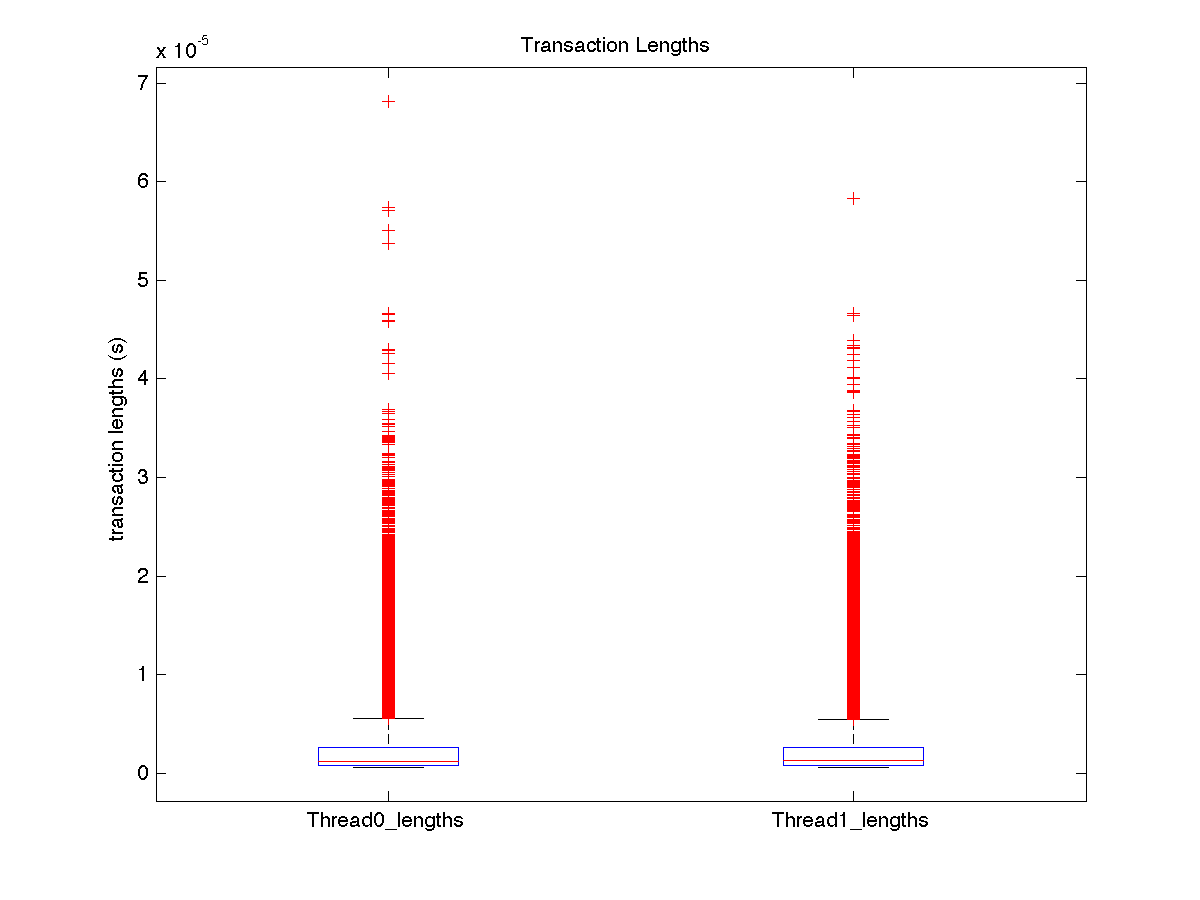
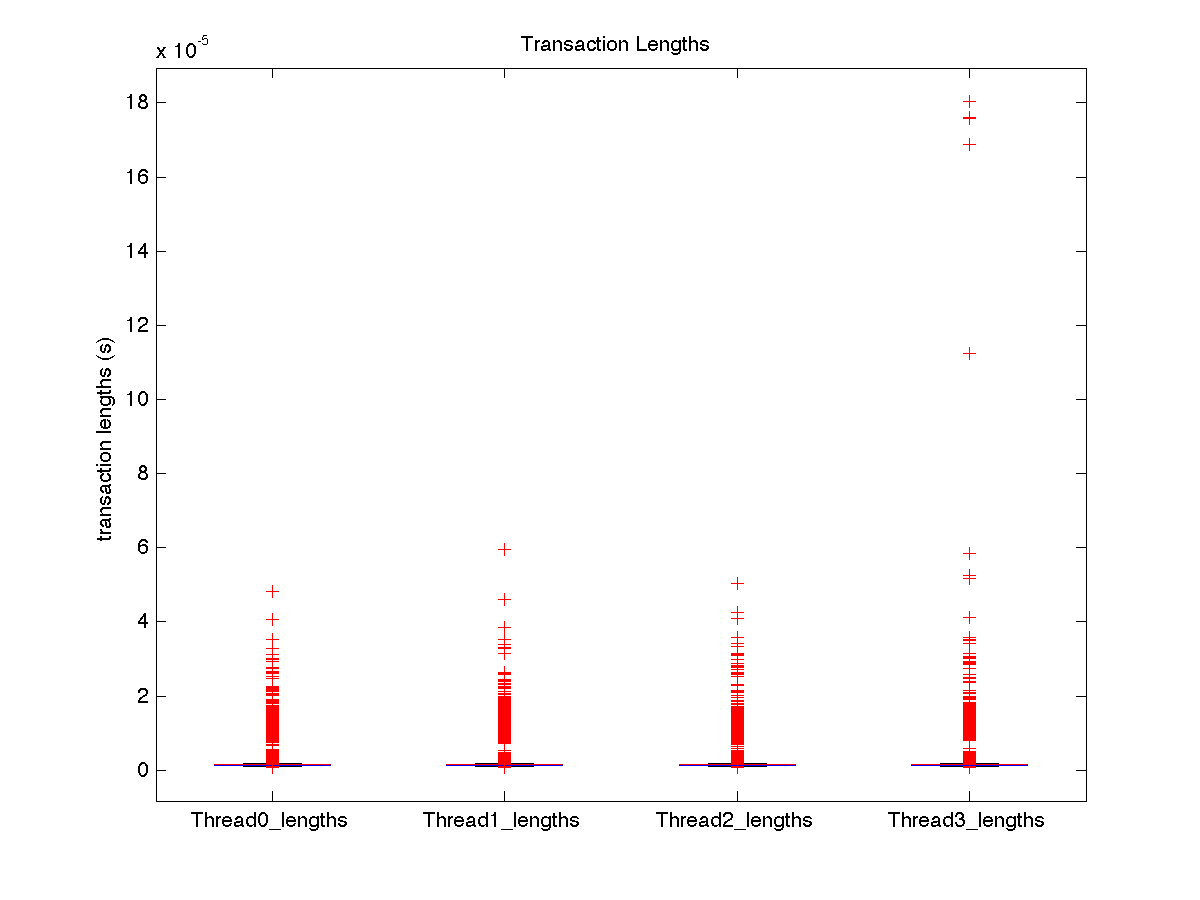
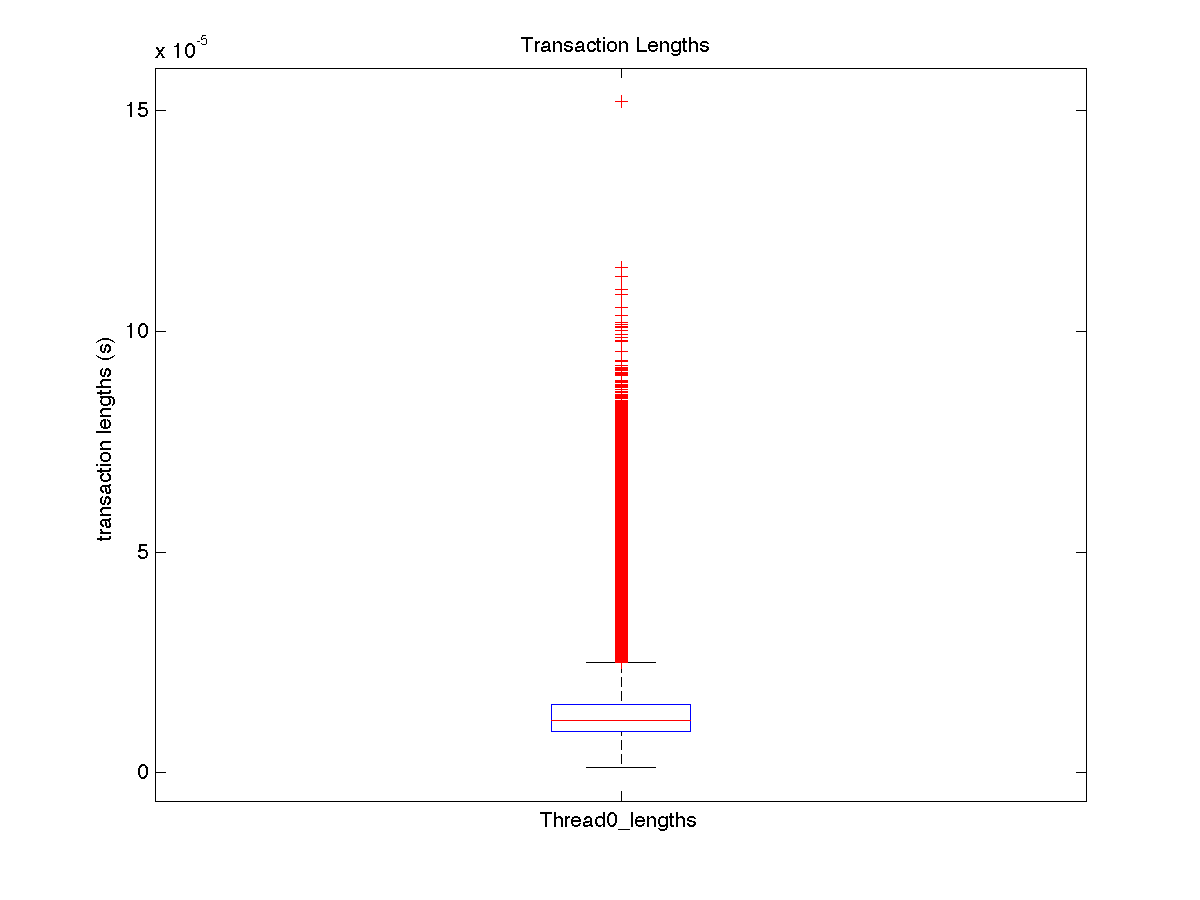
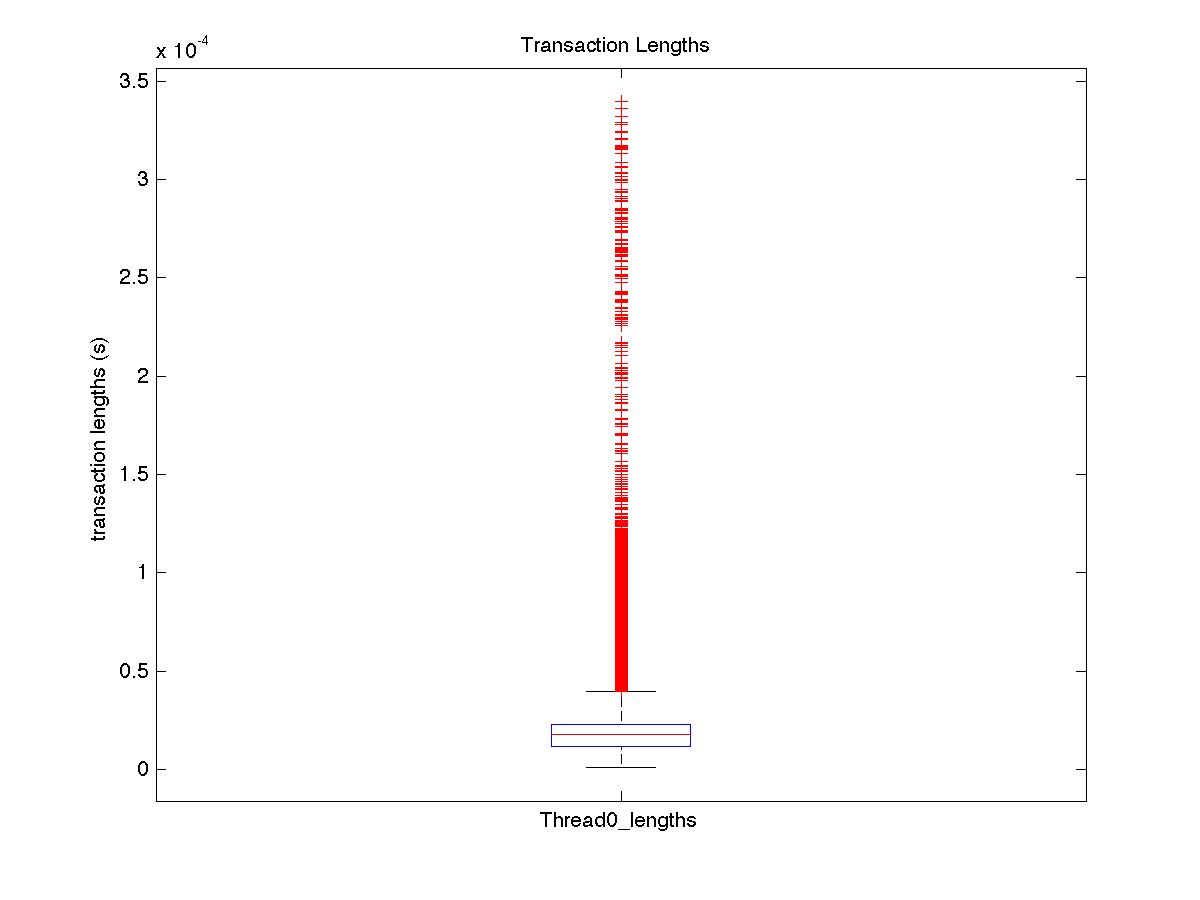
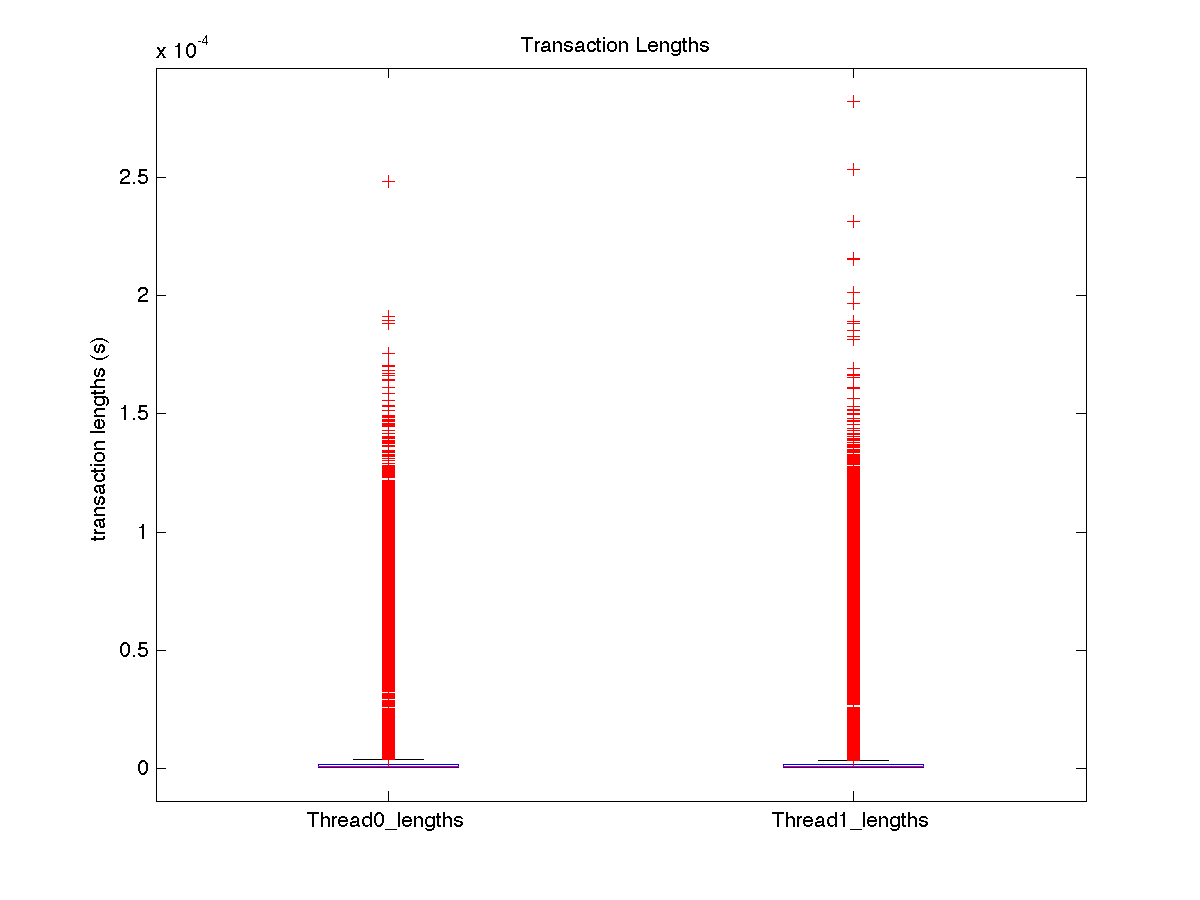
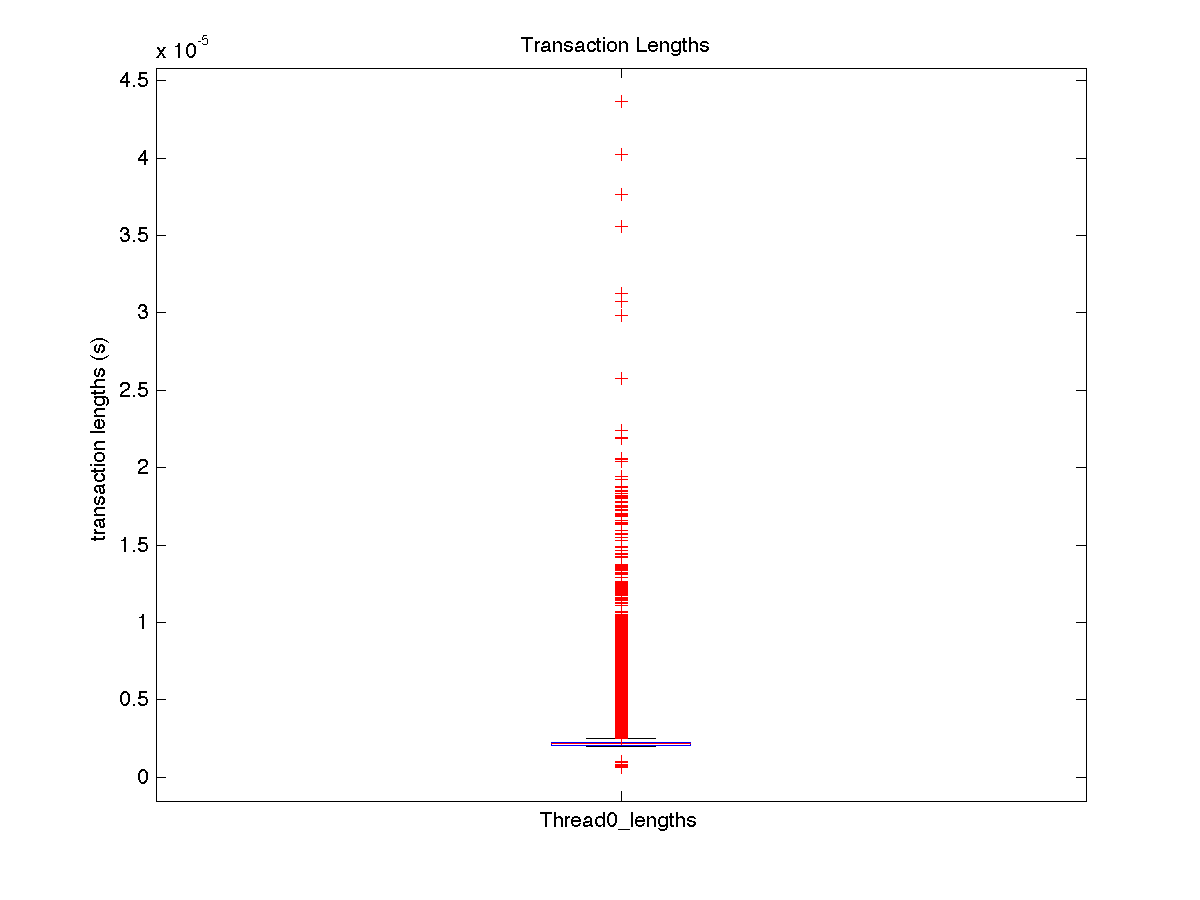
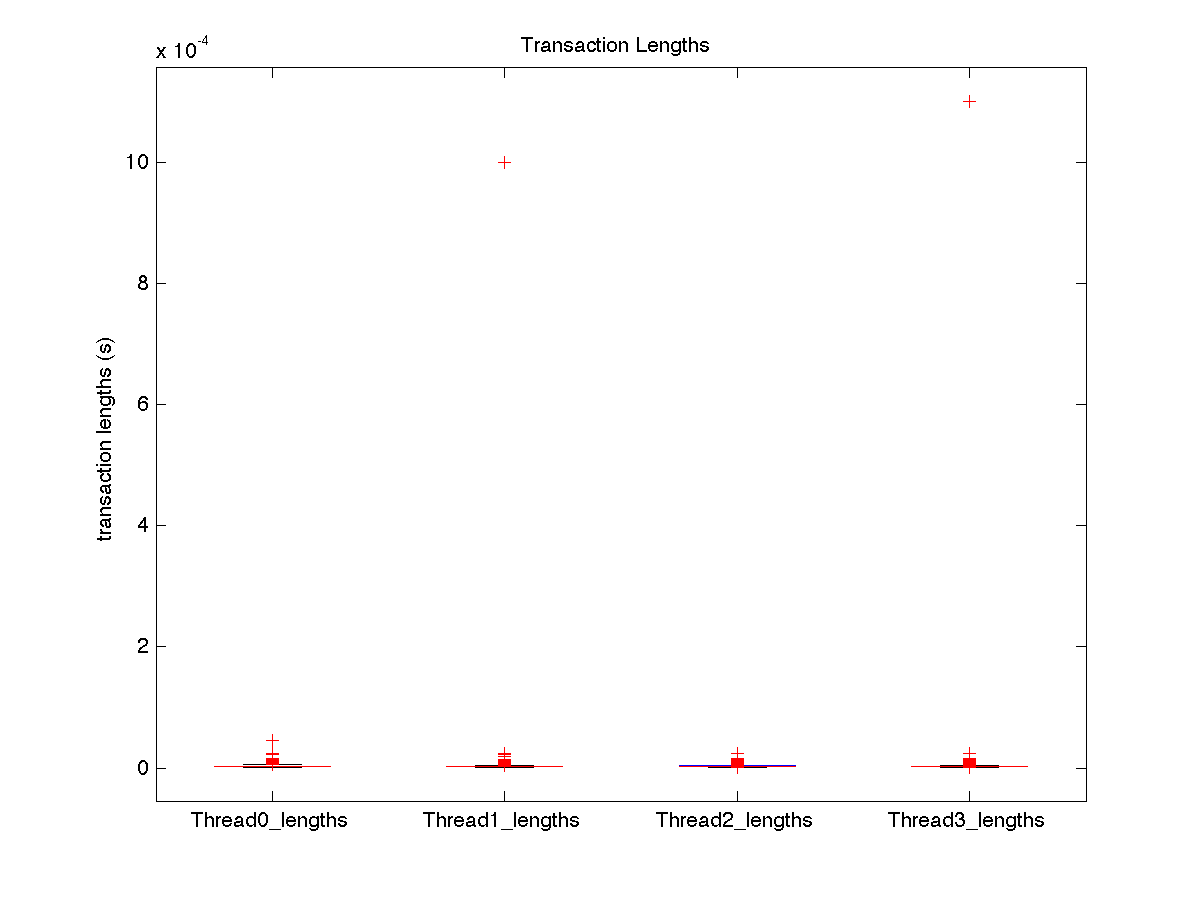
| Low contention - Boxplot of entire distribution for 1 thread |
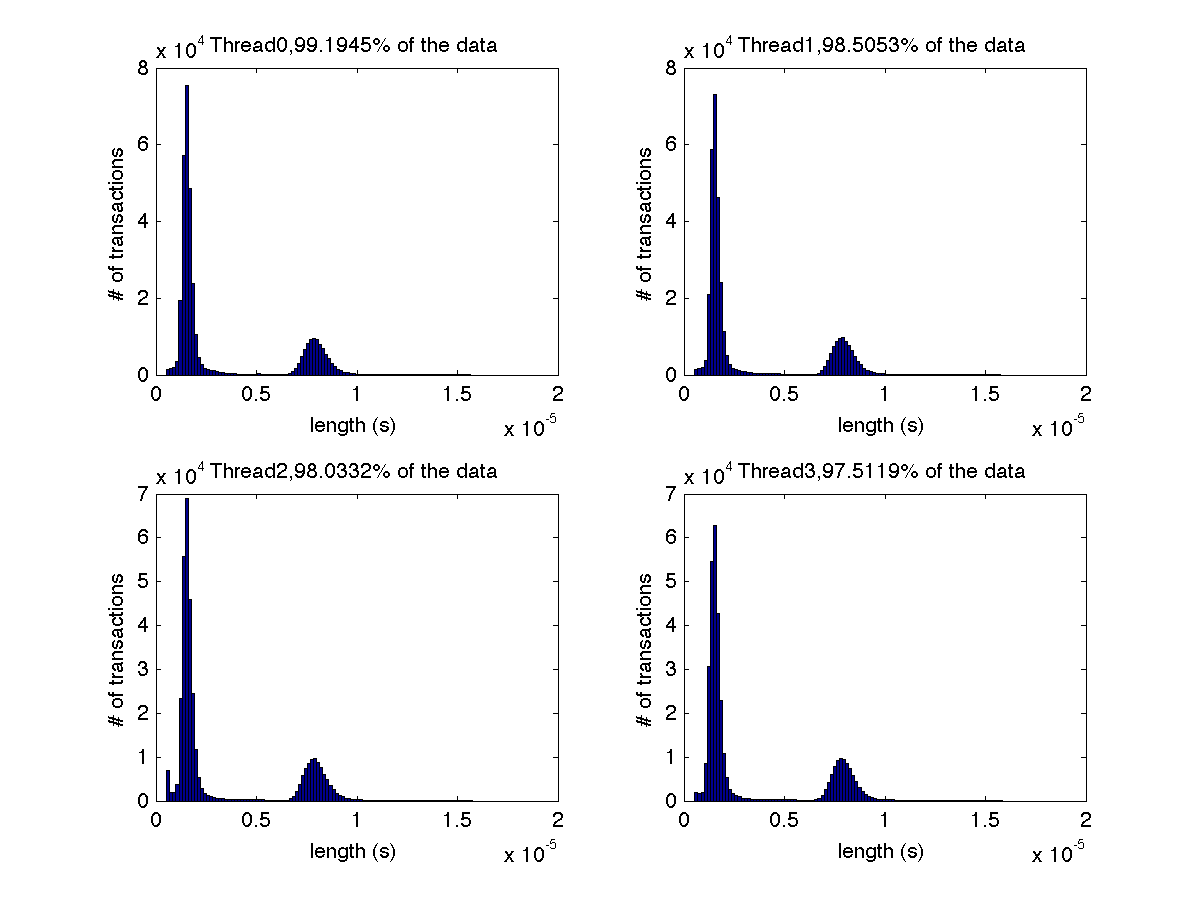
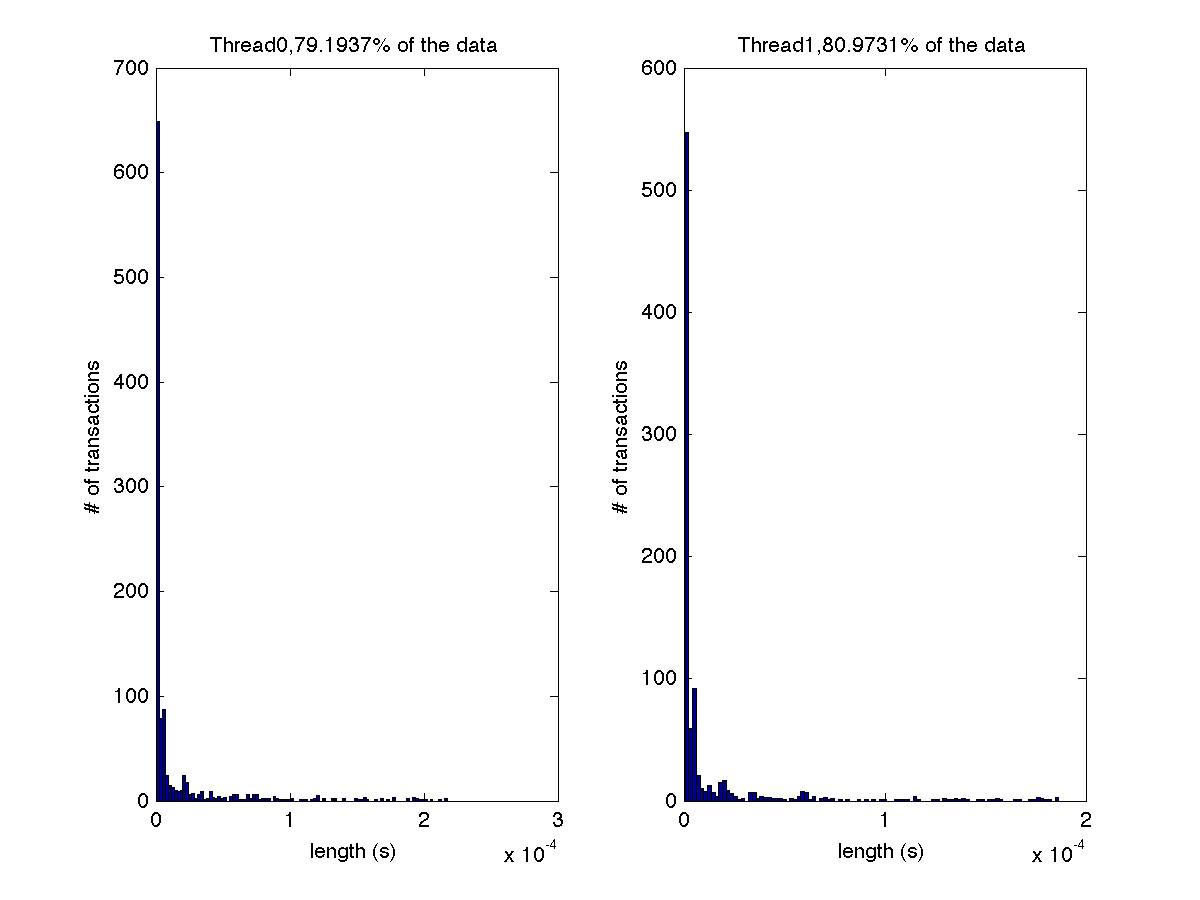
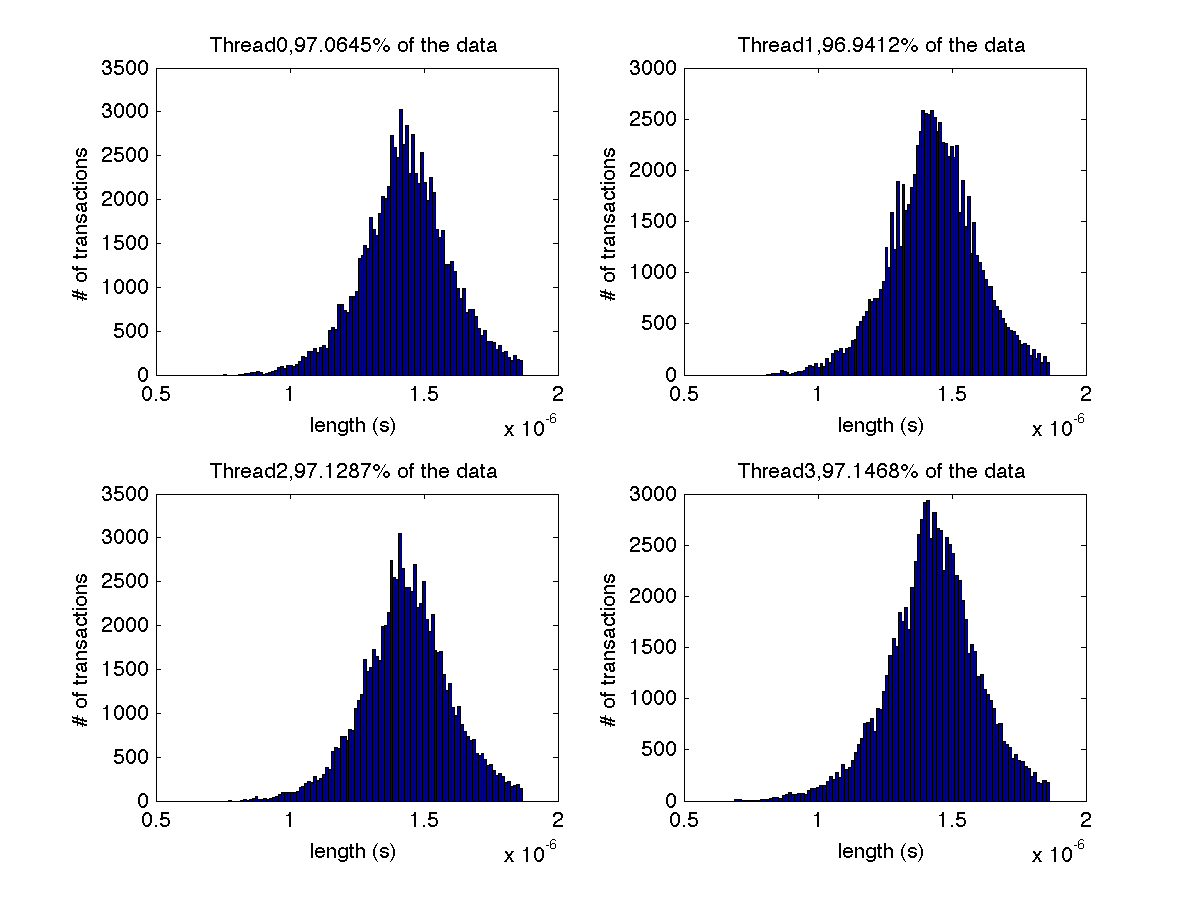
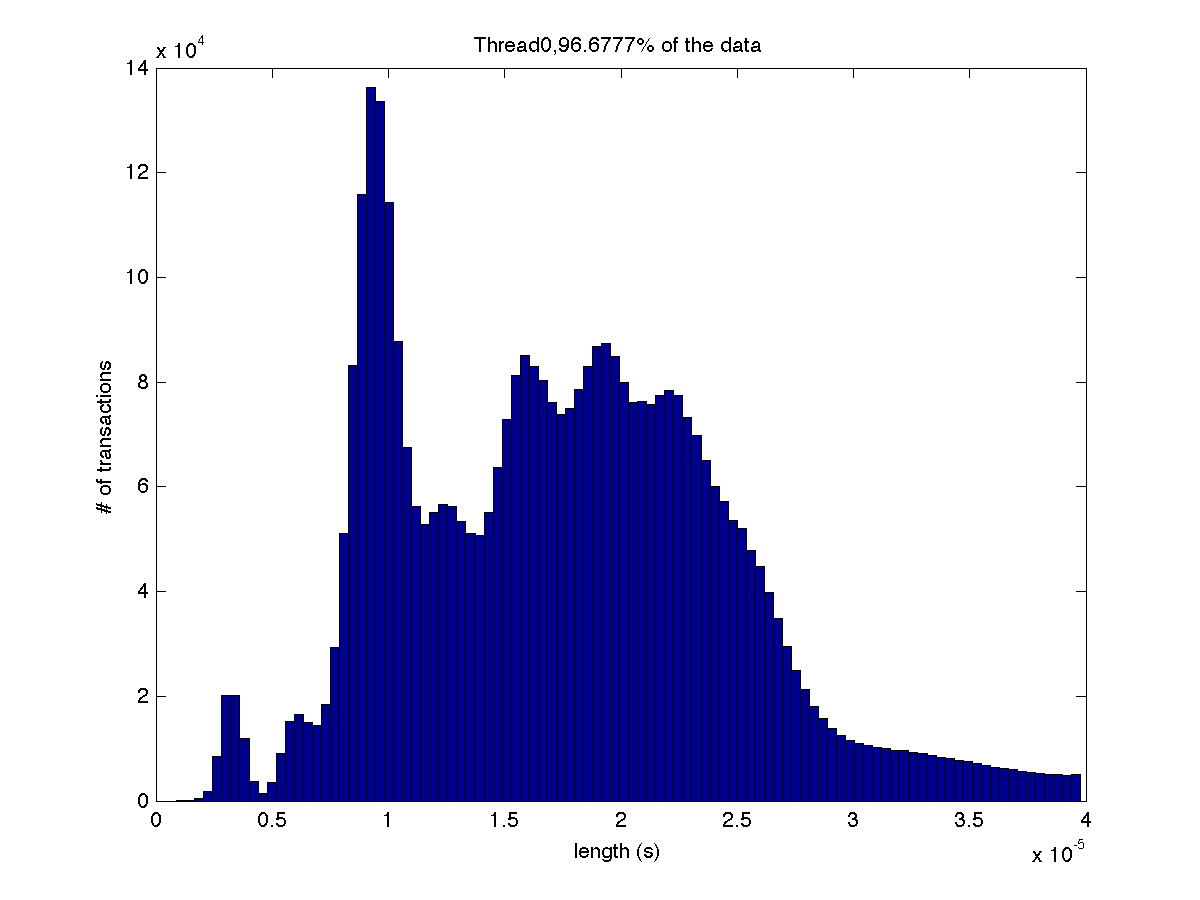
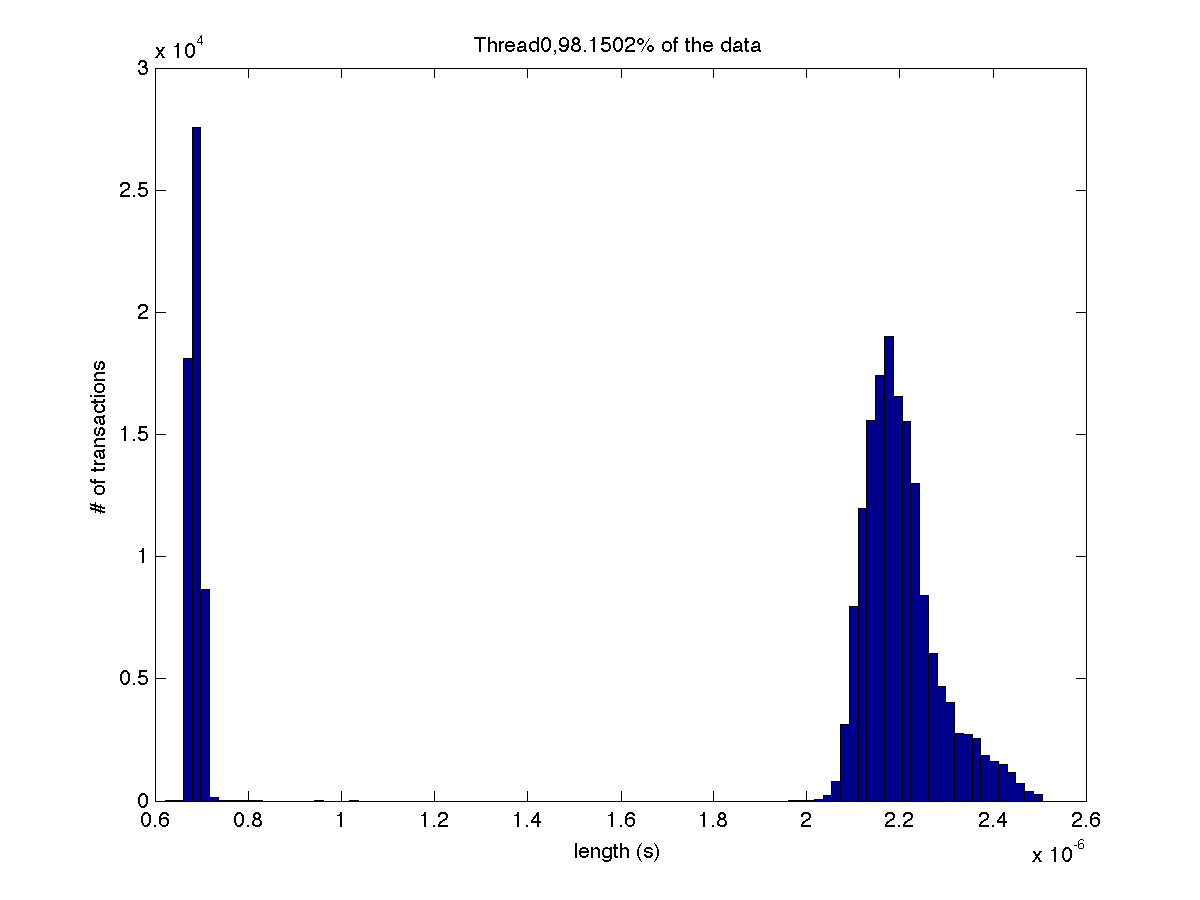
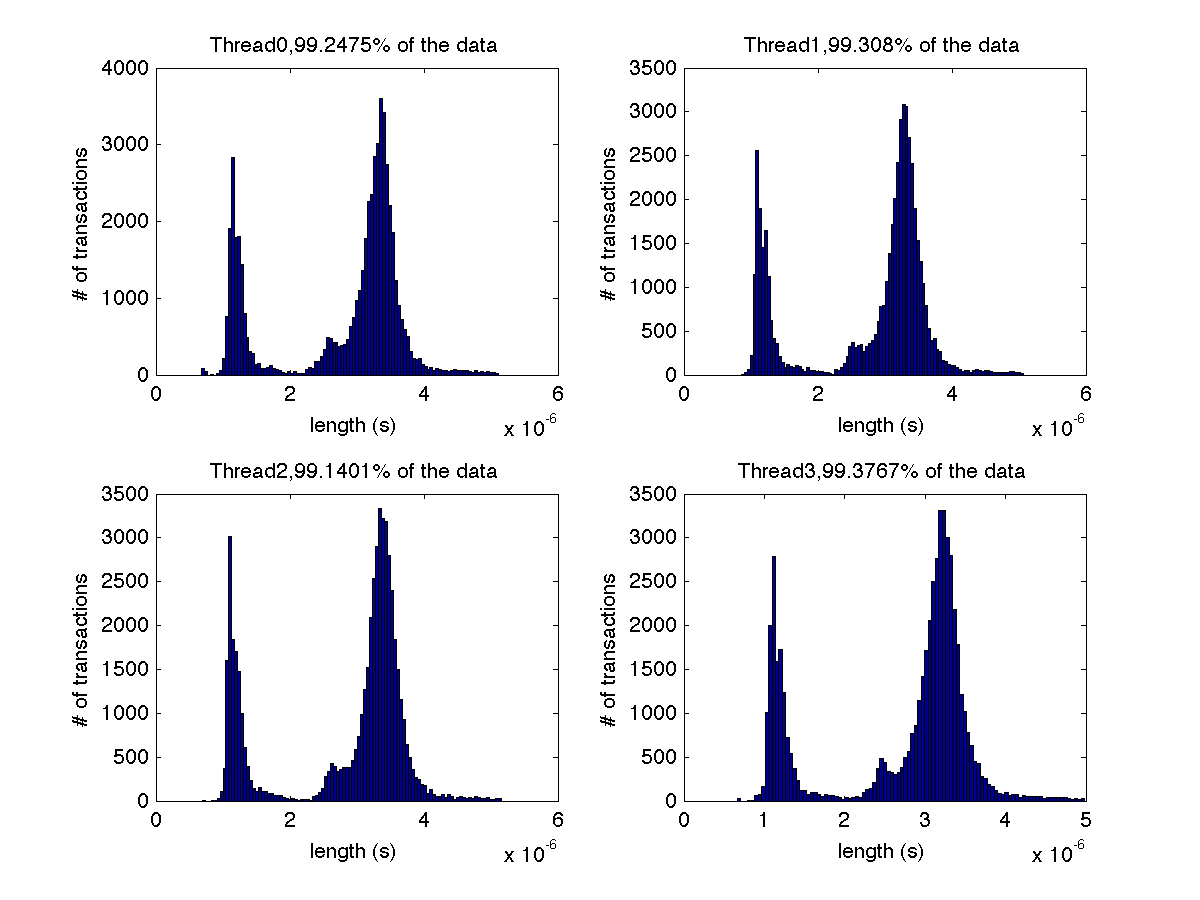
Low contention - Histogram showing majority lengths of transactions for 1 thread (exact percentage in title of graph) |
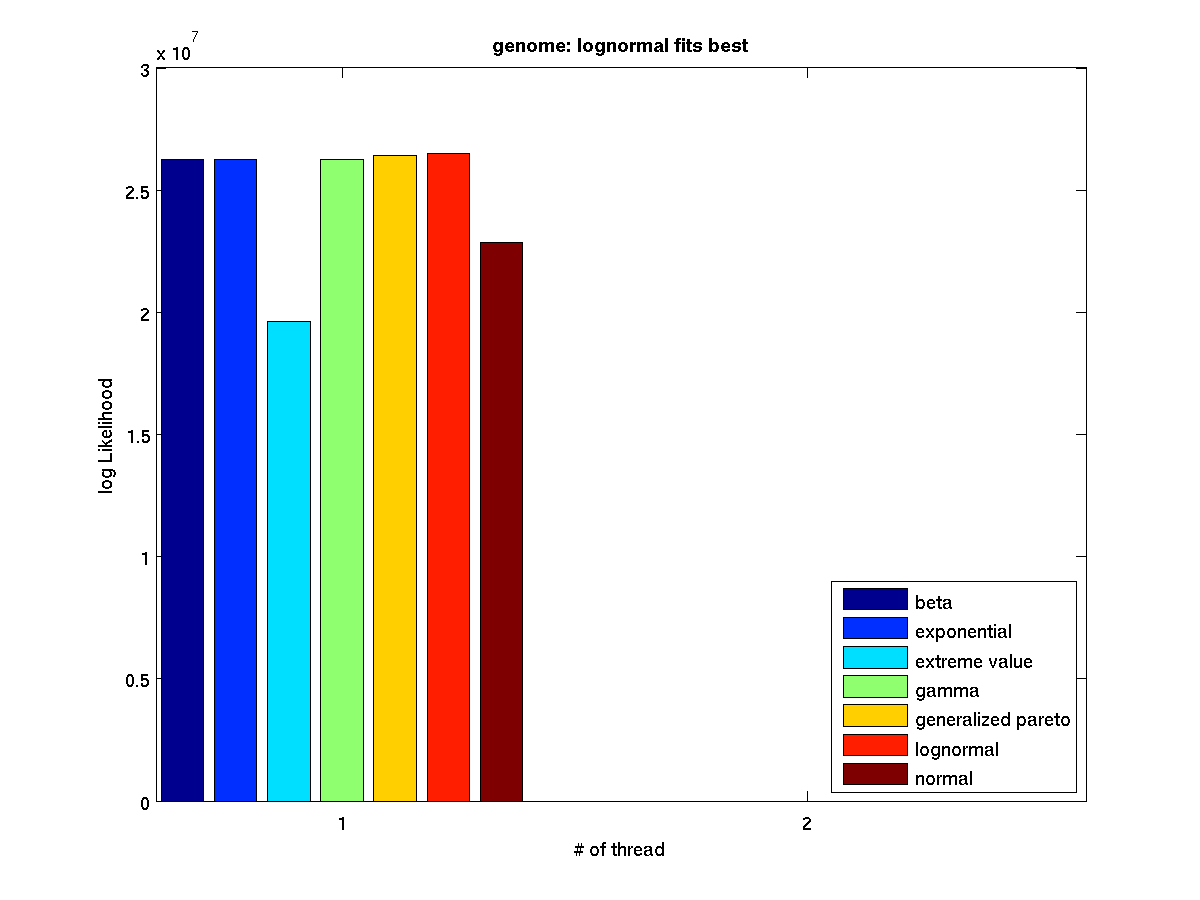
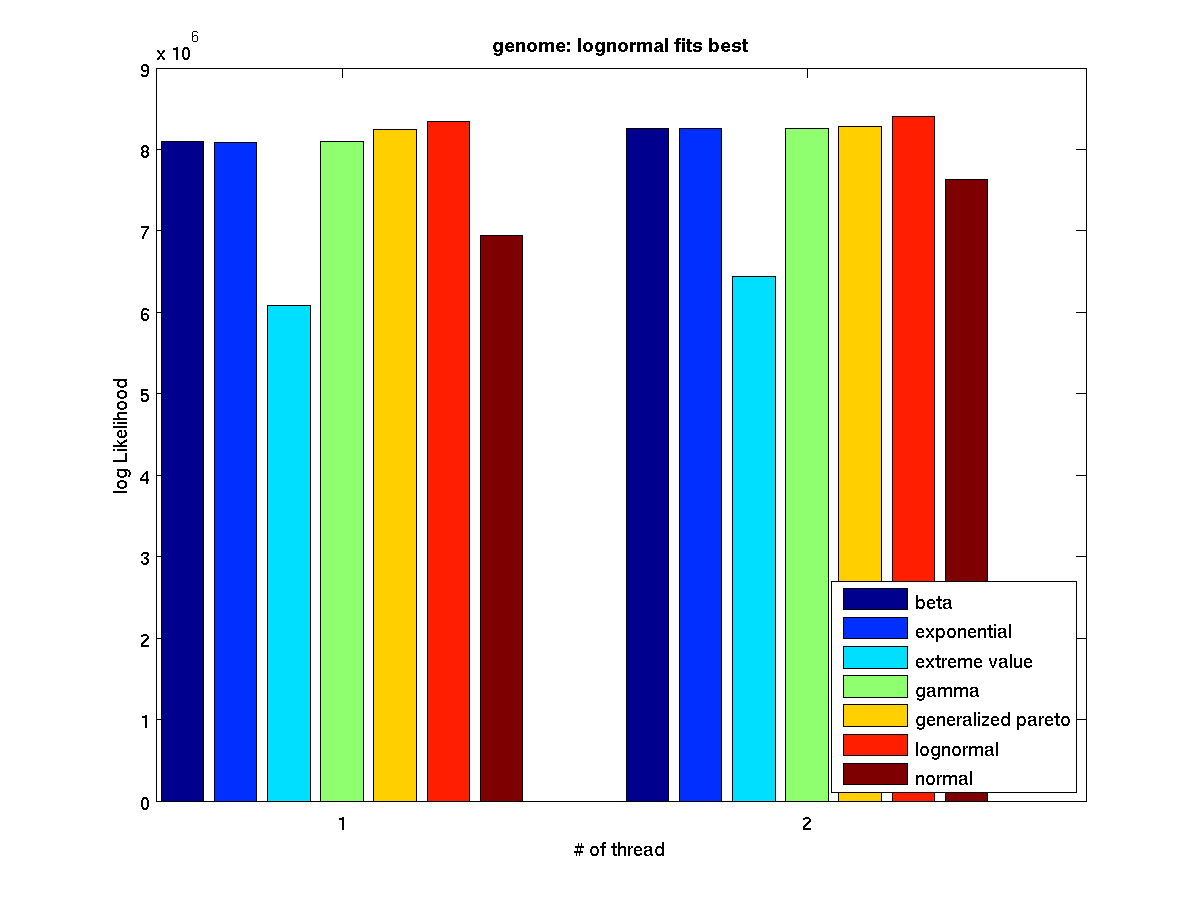
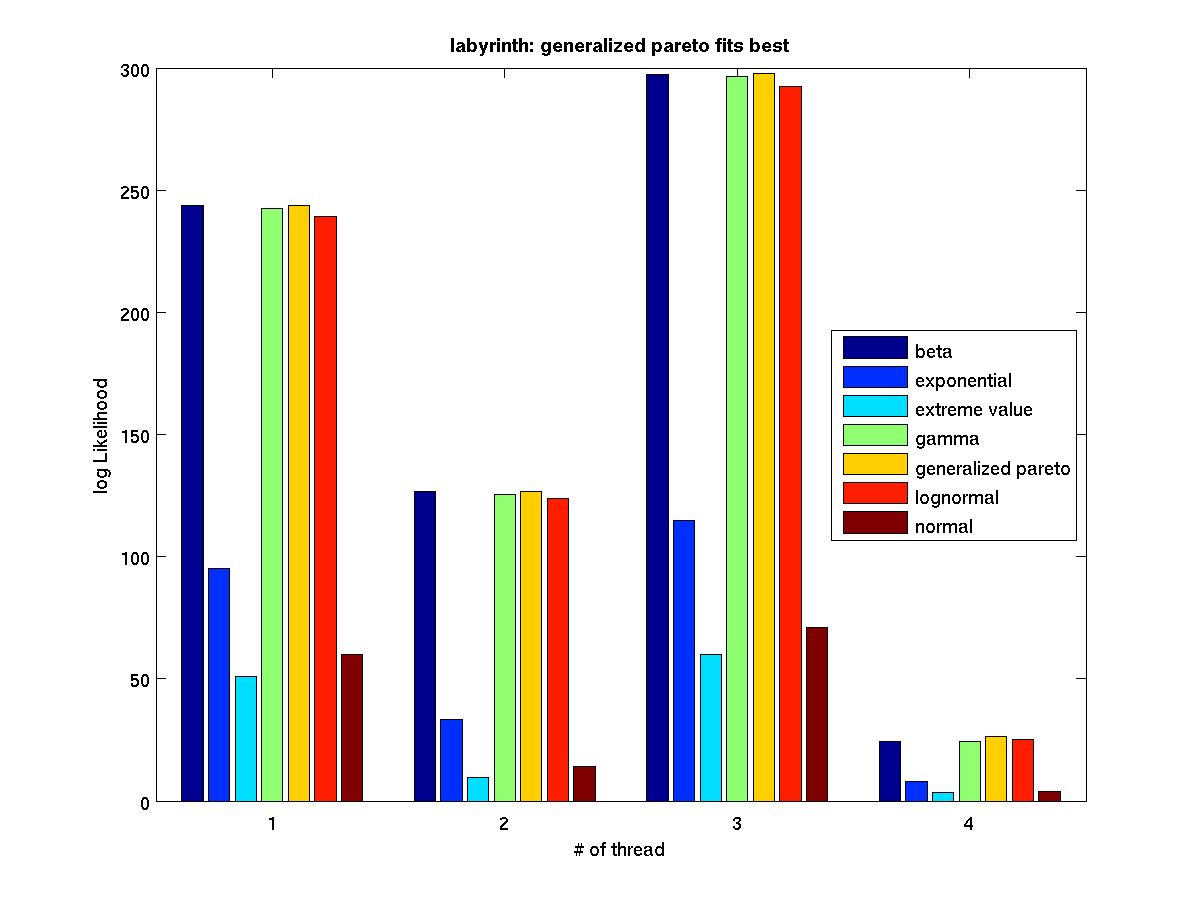
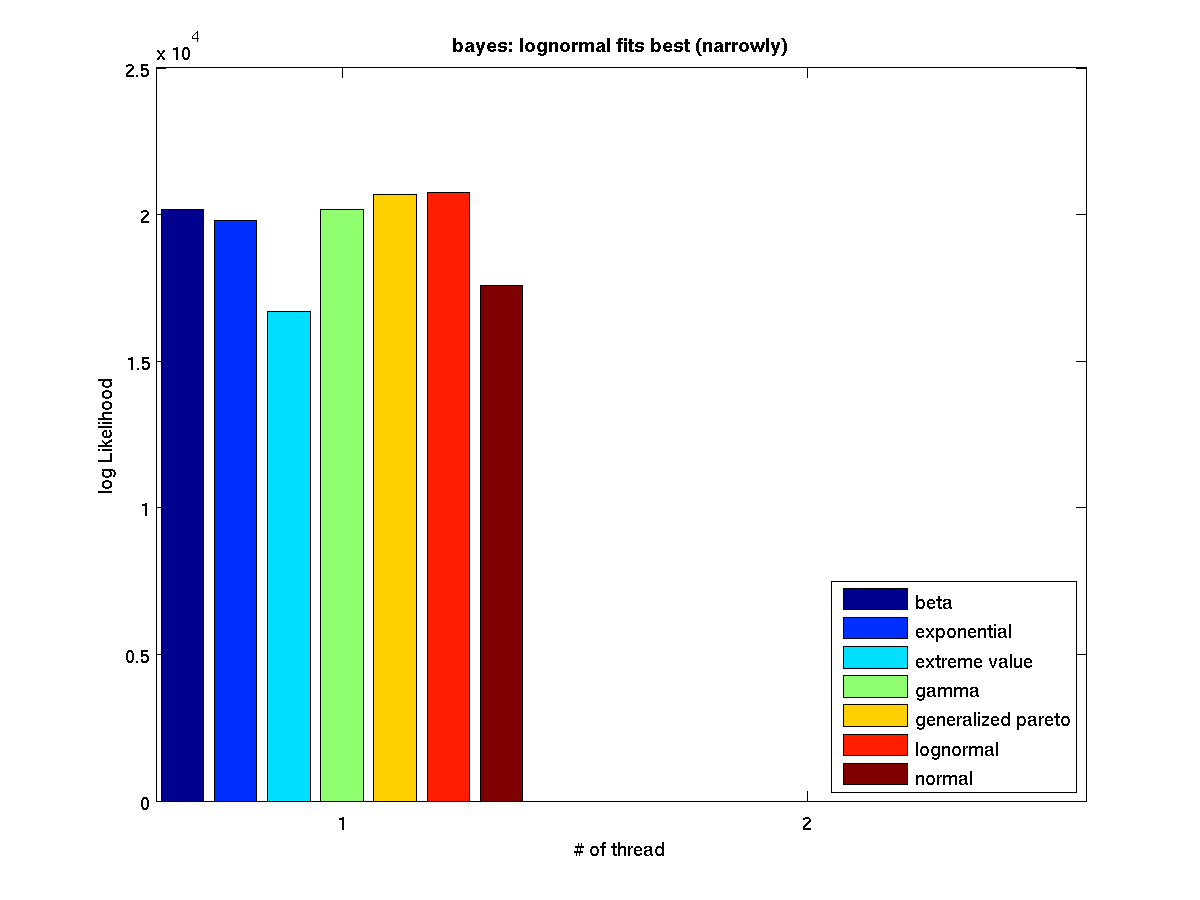
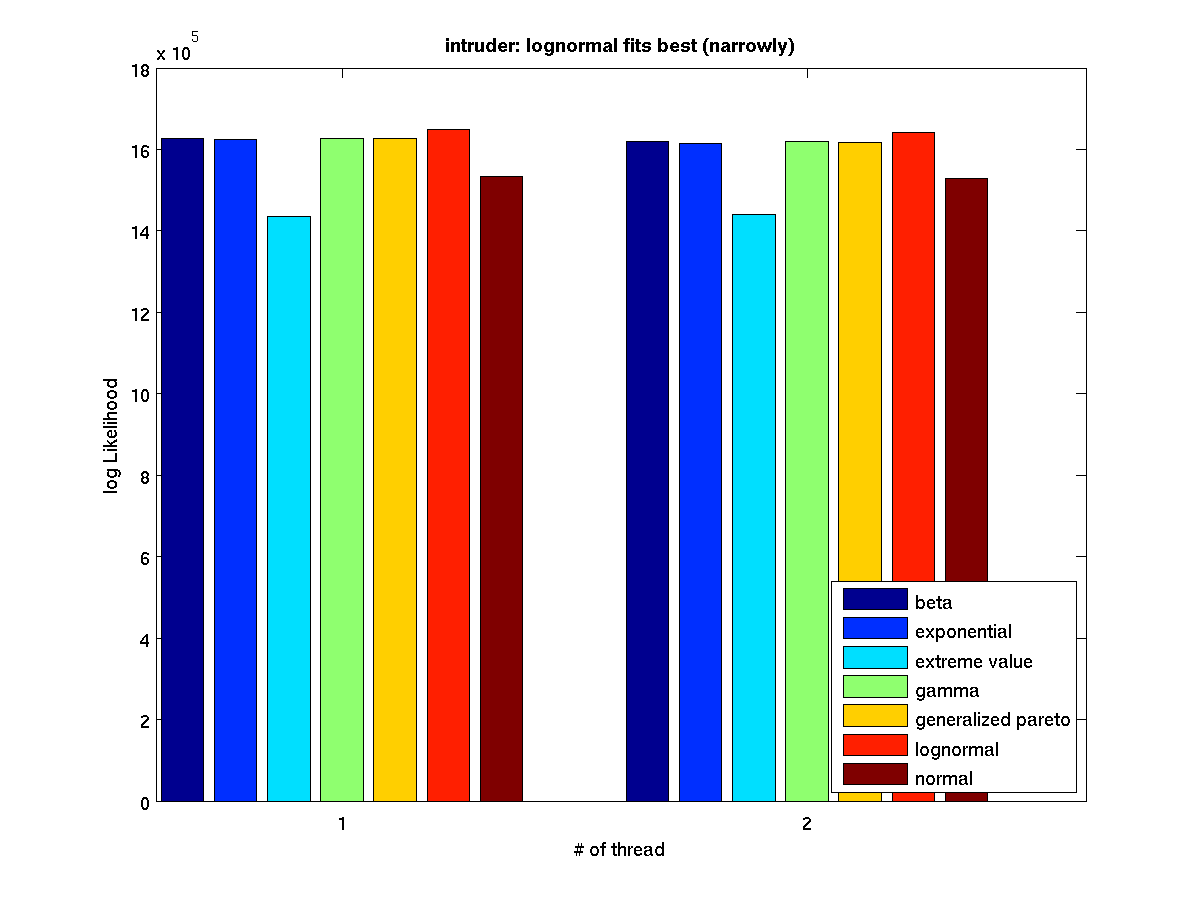
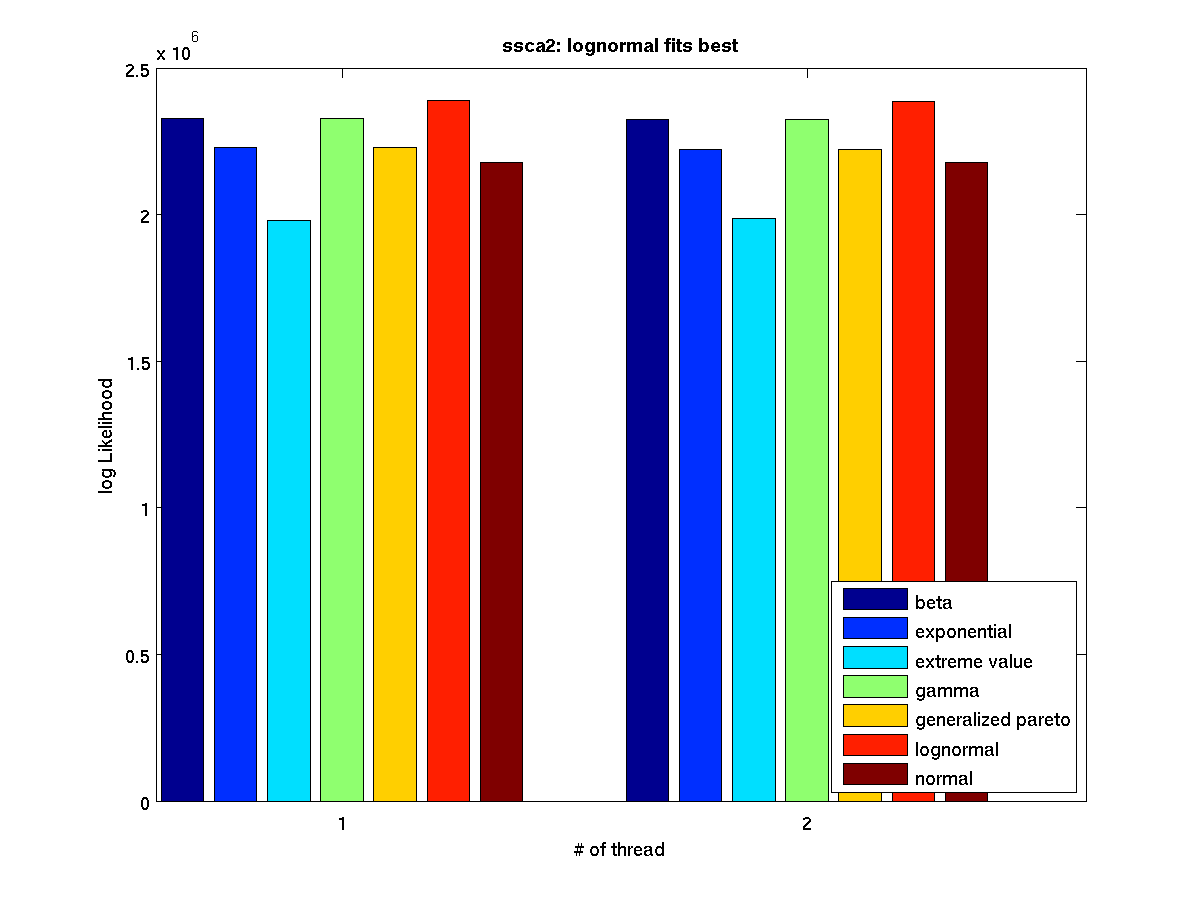
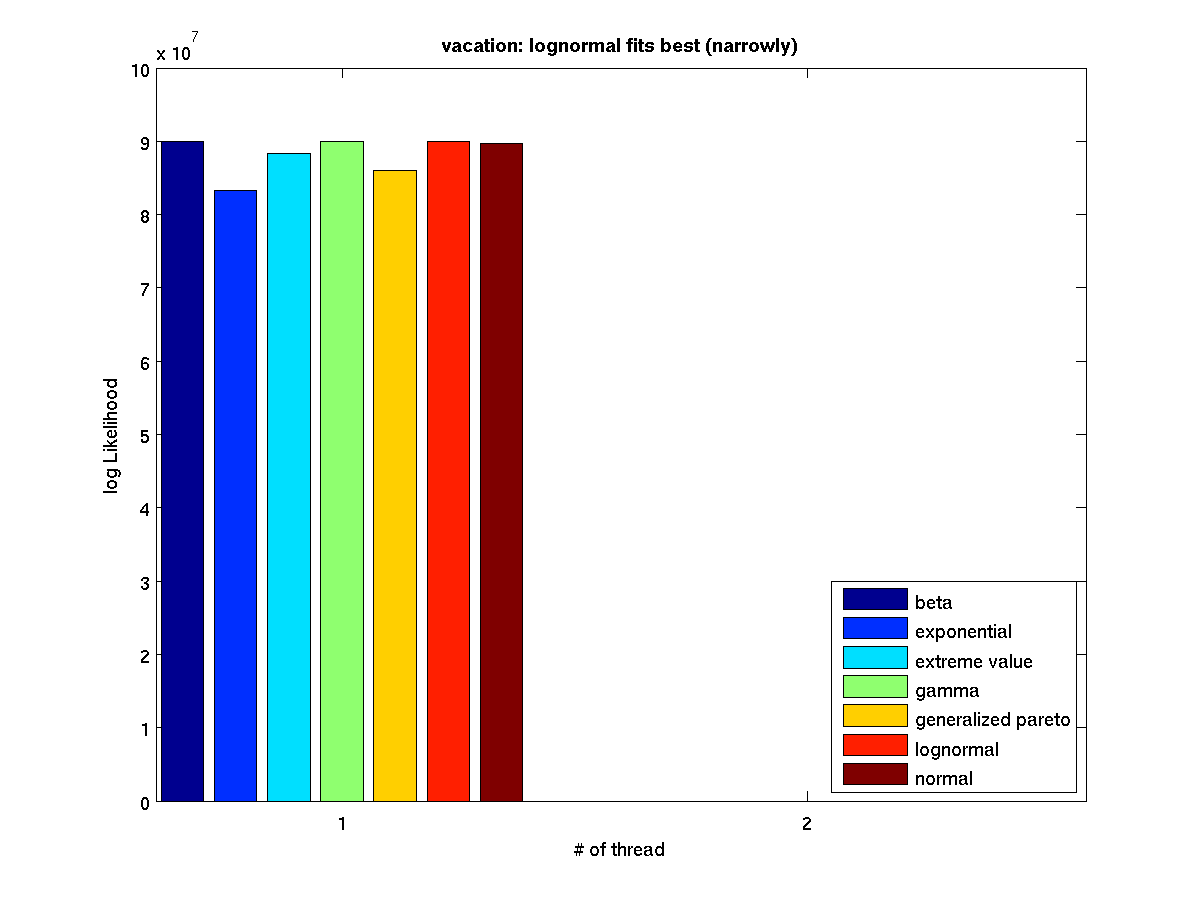
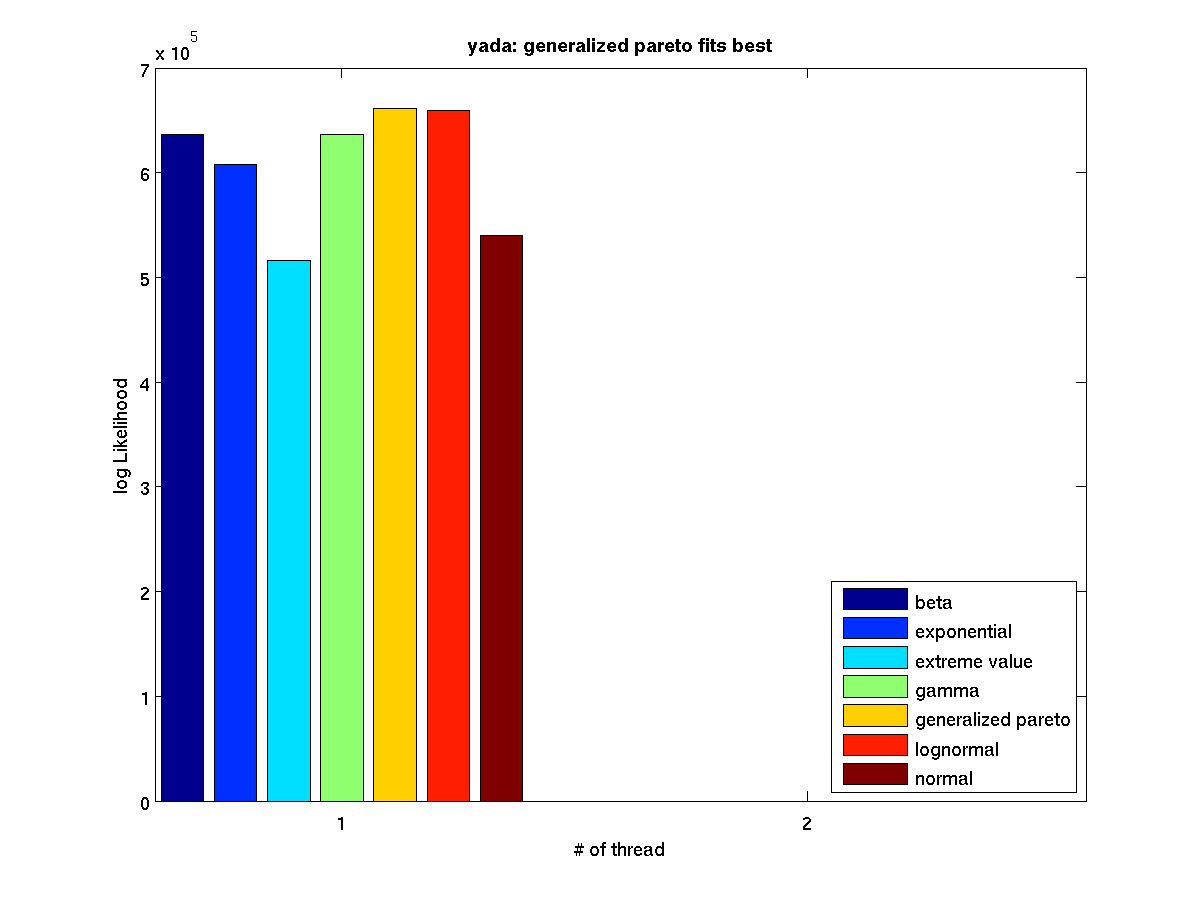
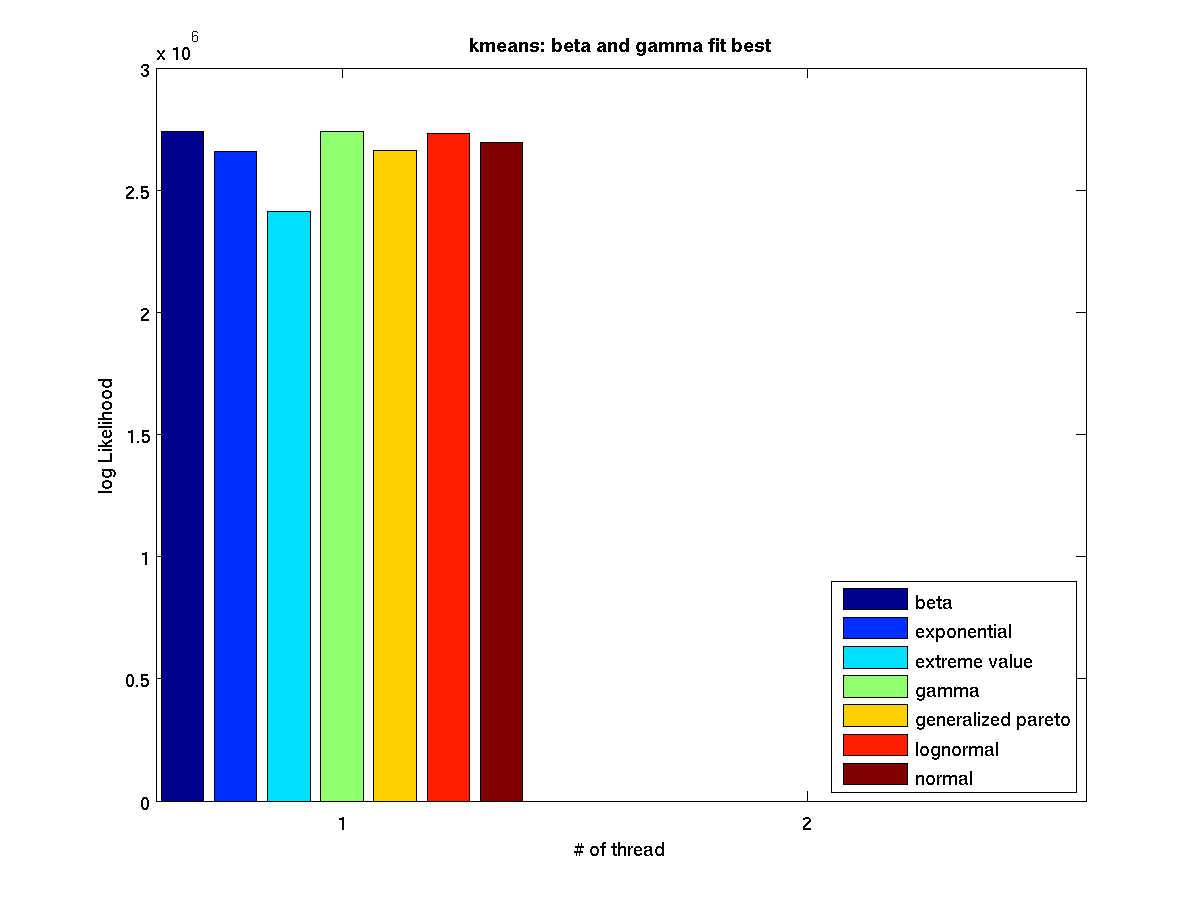
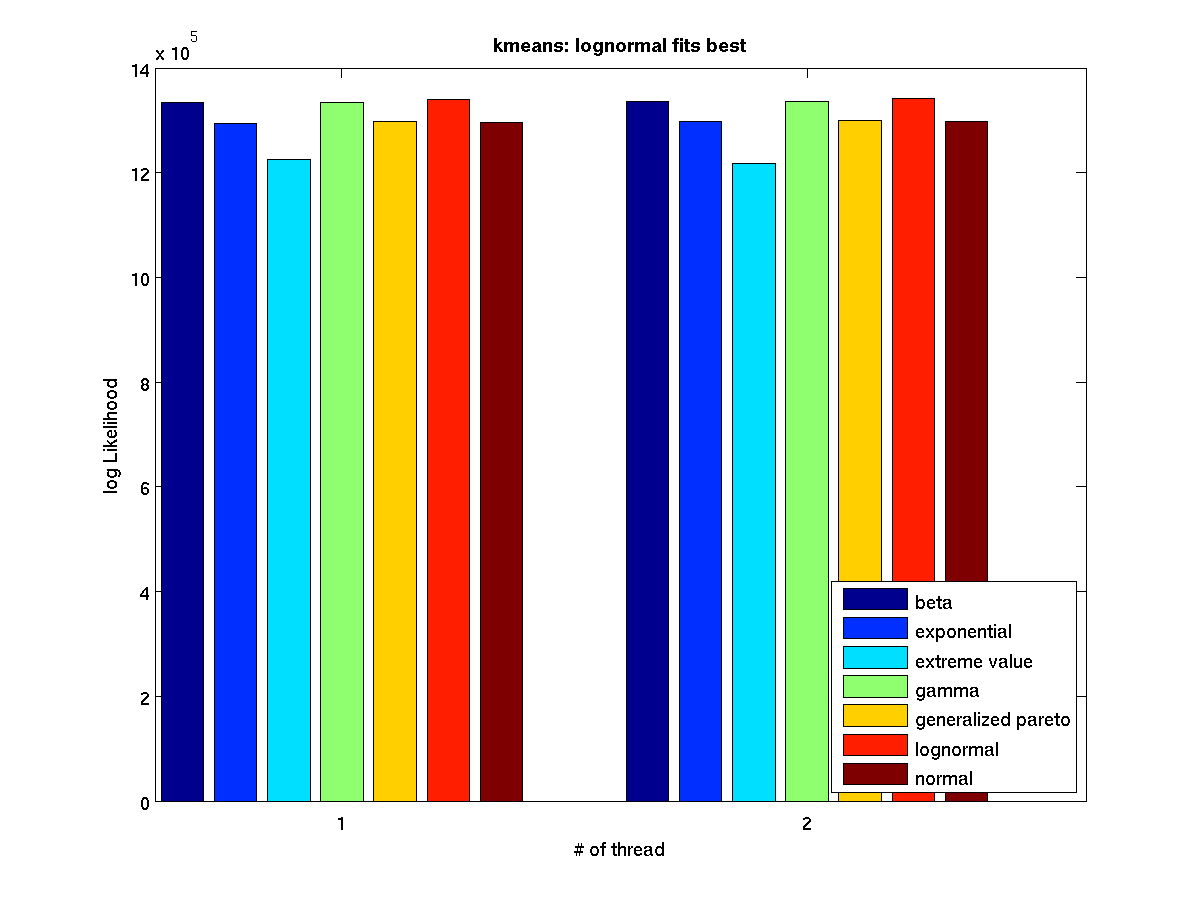
Low contention - Bar graph of log-likelihood values for 1 thread |
| |
 |
 |
 |
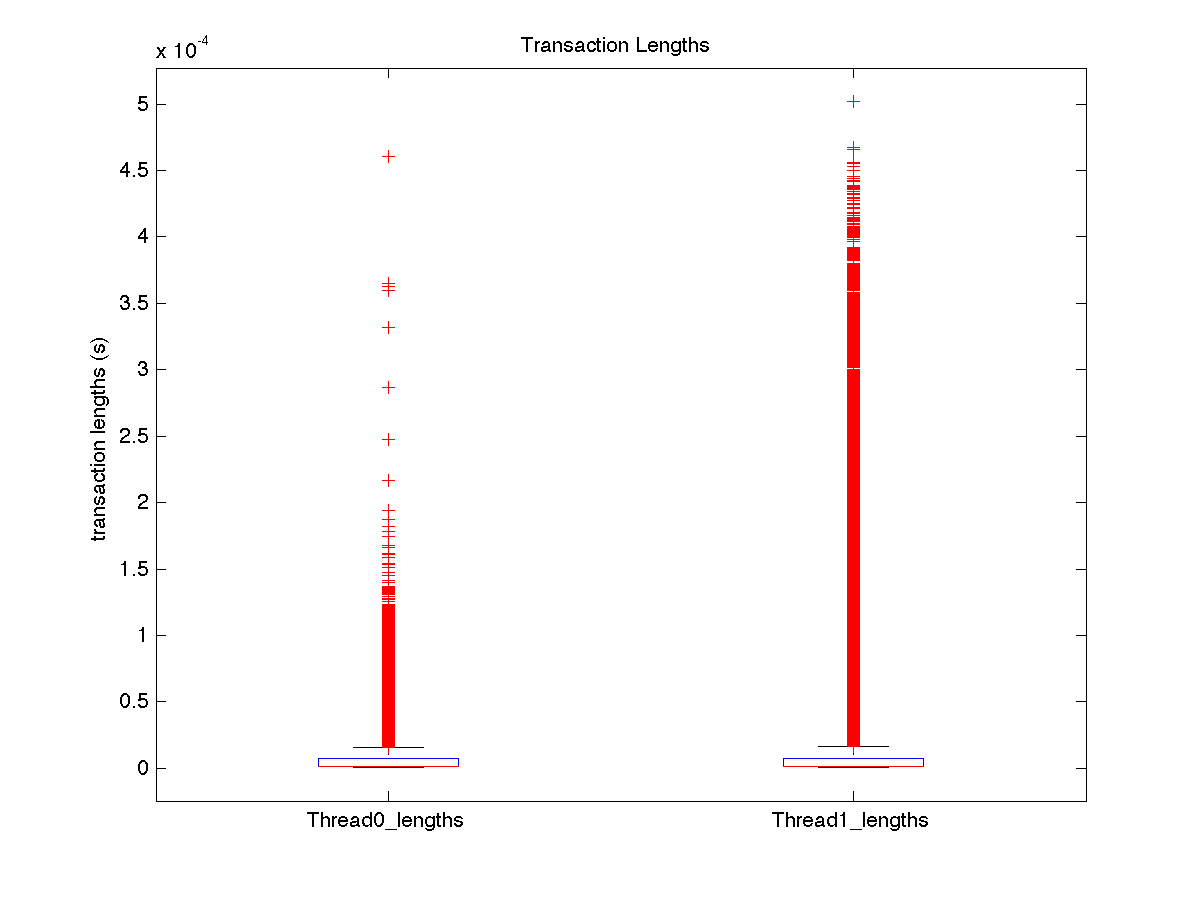
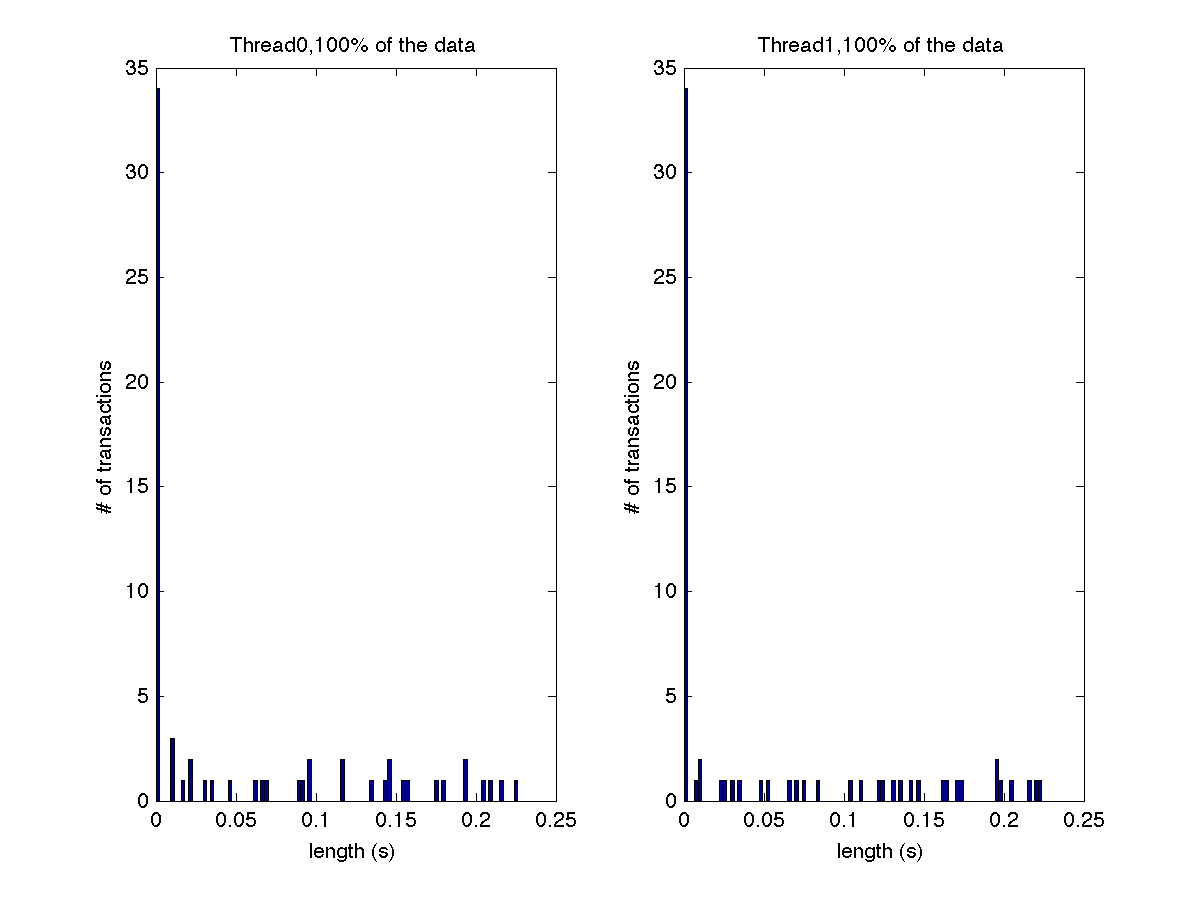
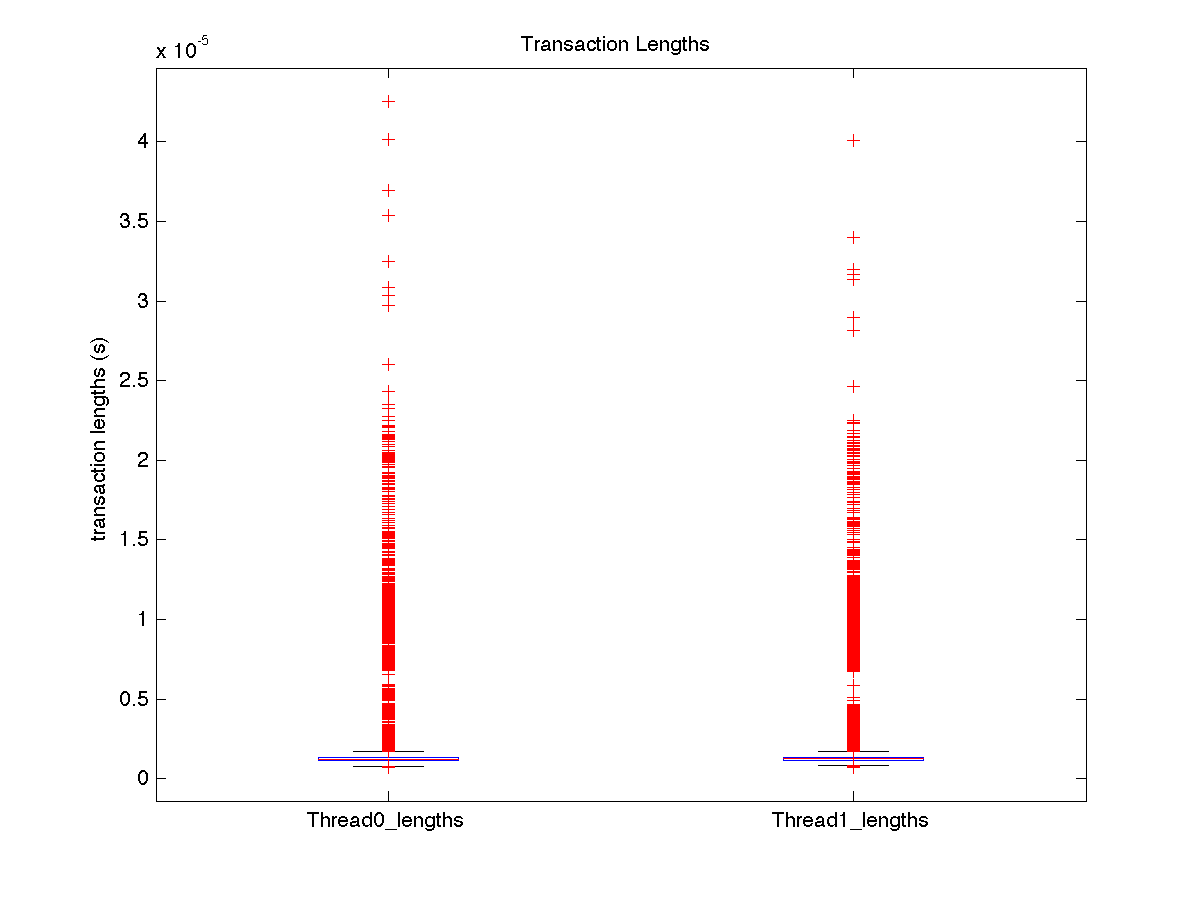
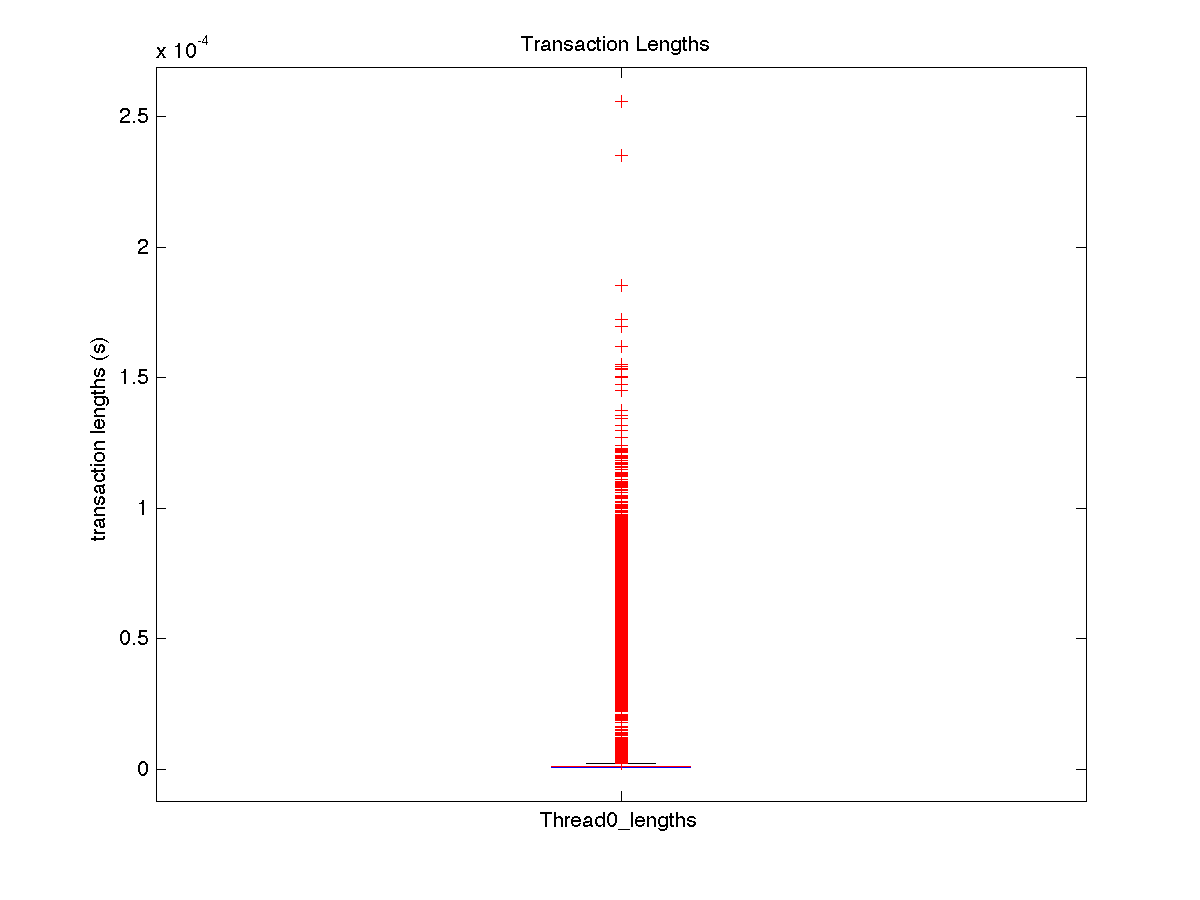
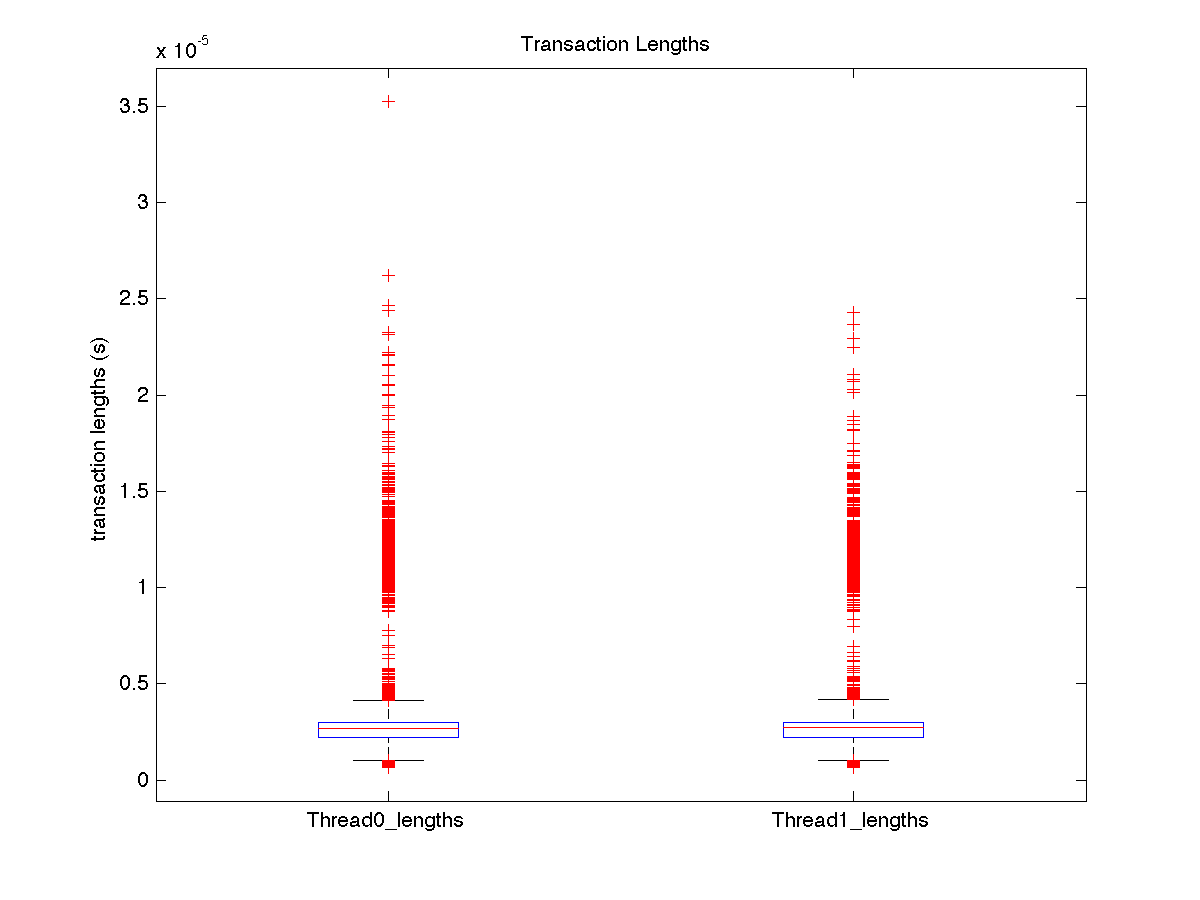
| Low contention - Boxplot of entire distribution for 2 threads |
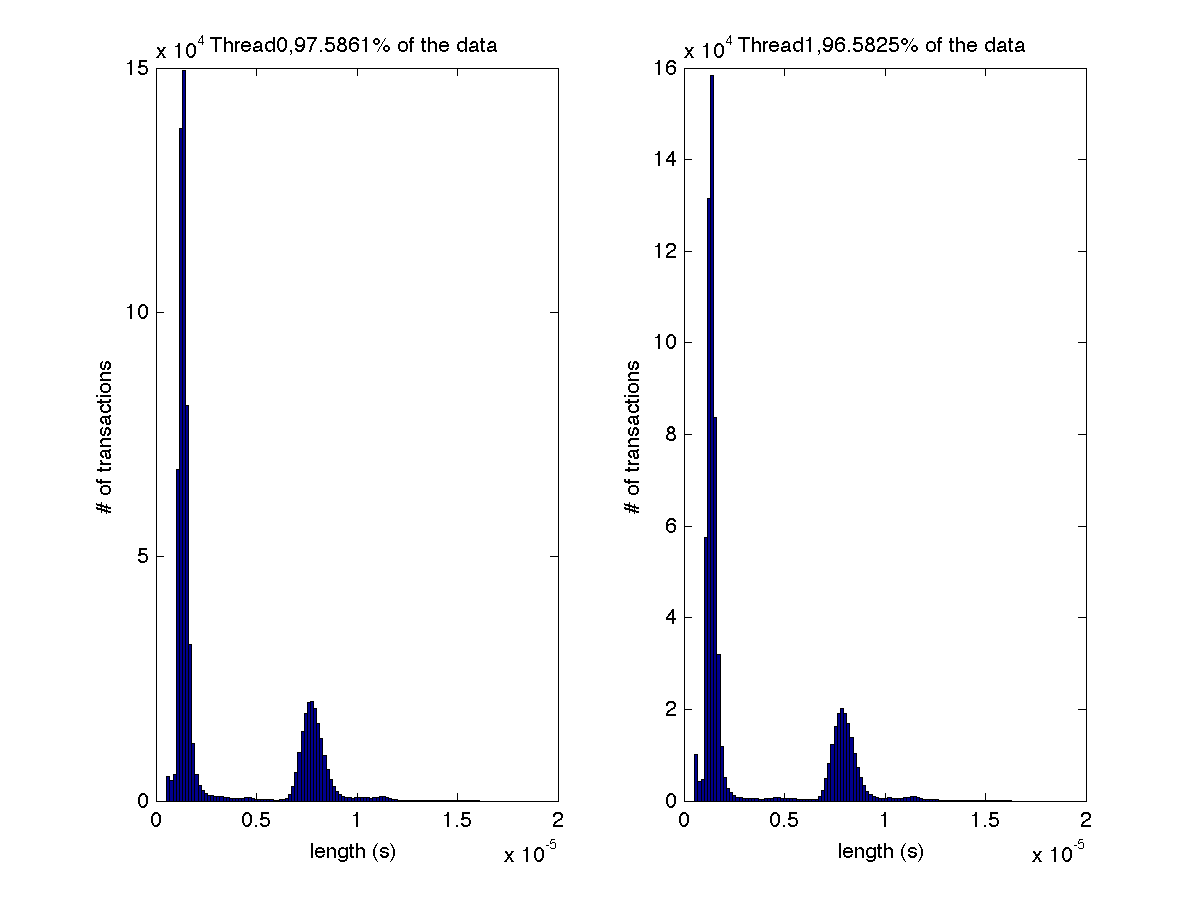
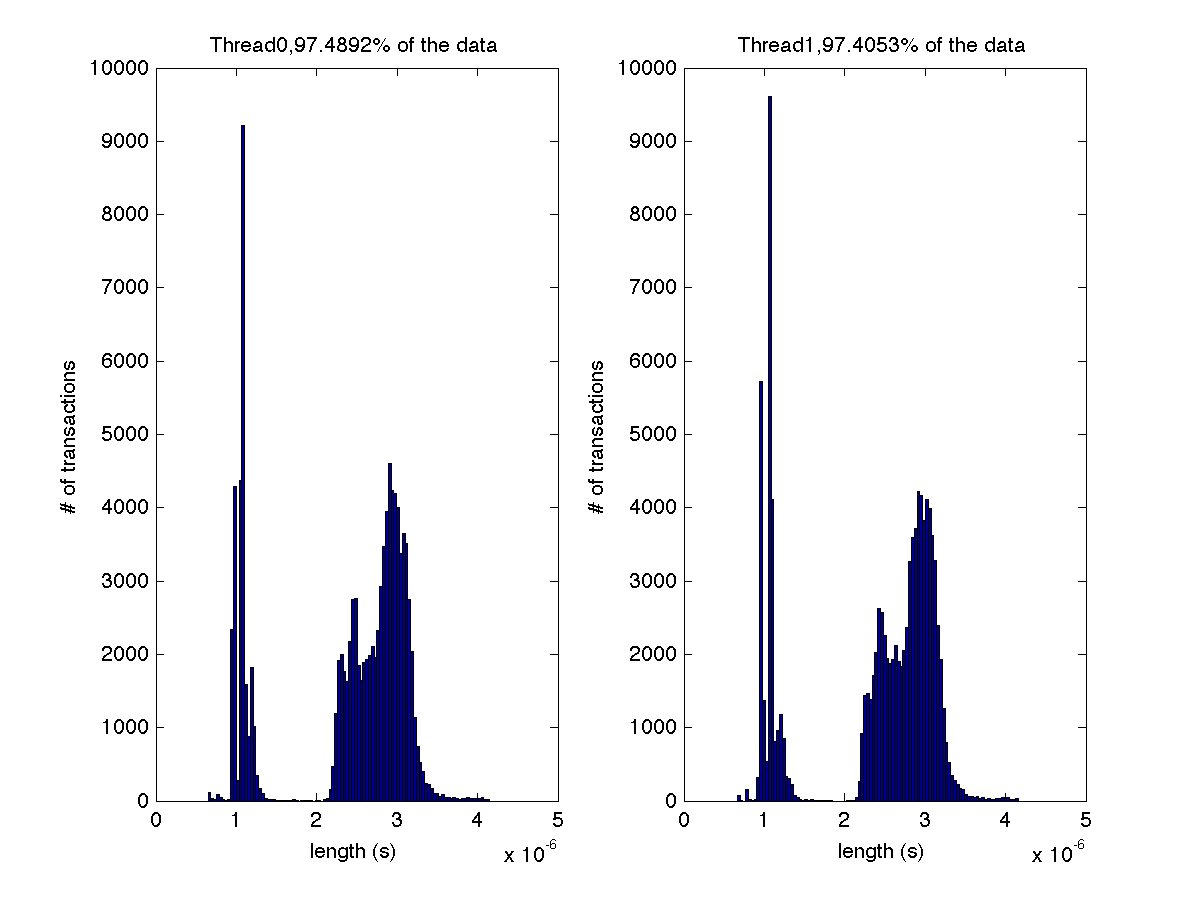
Low contention - Histogram showing majority lengths of transactions for 2 threads (exact percentages in title of graph) |
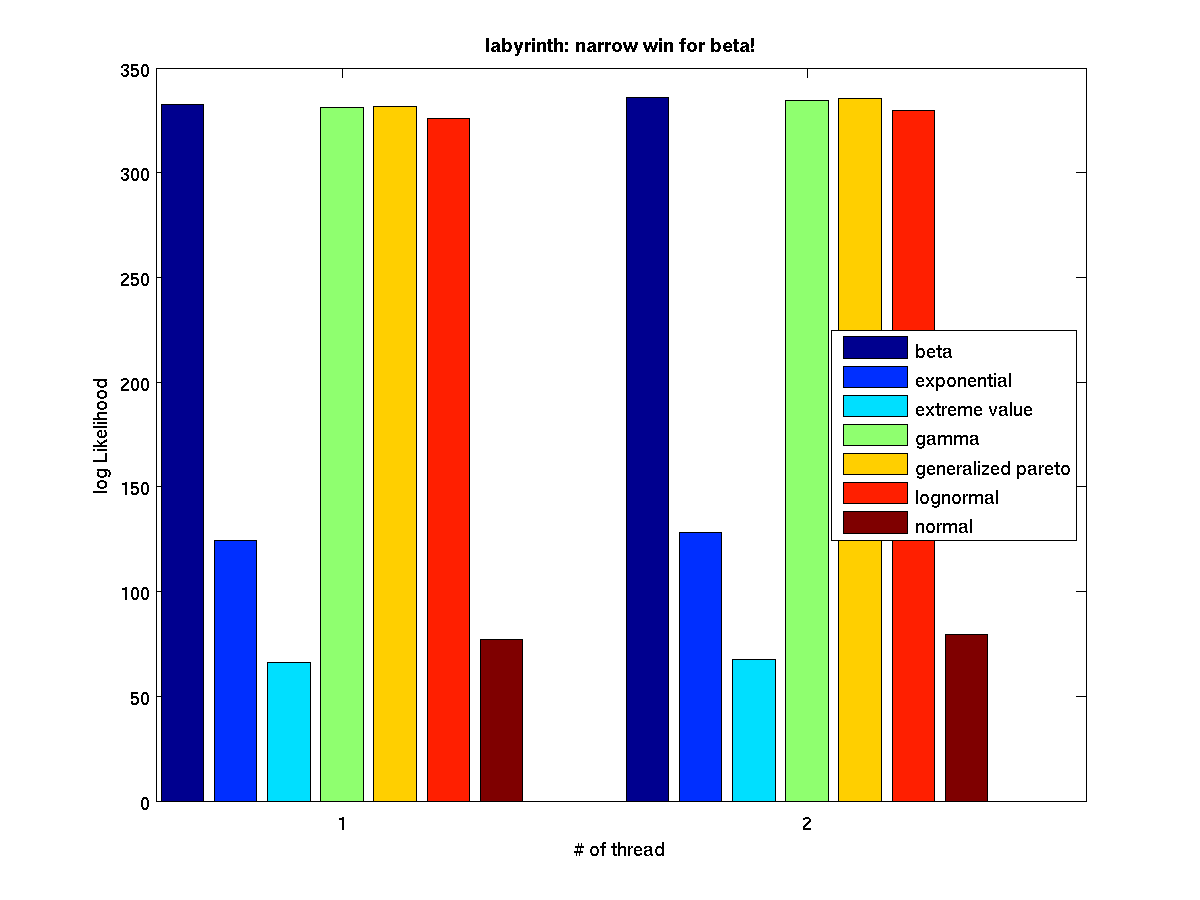
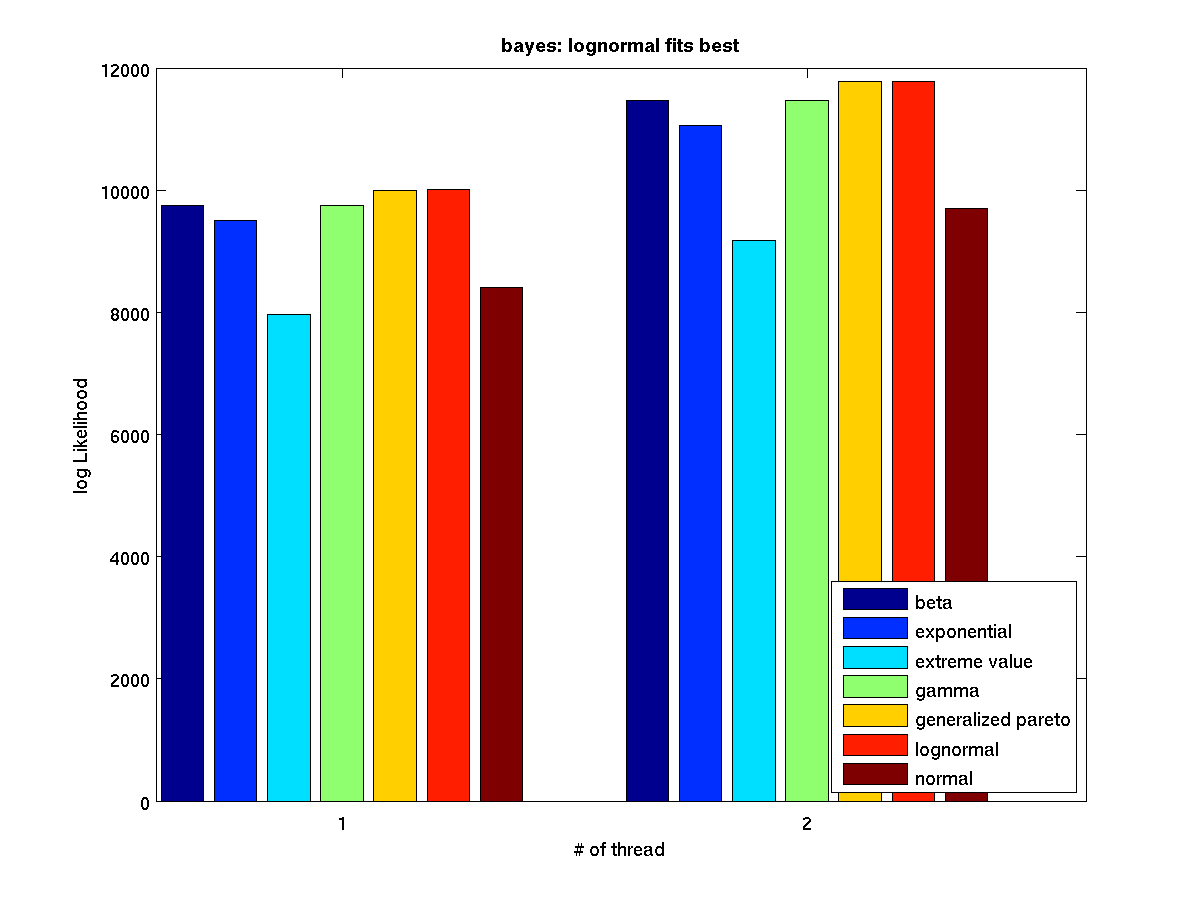
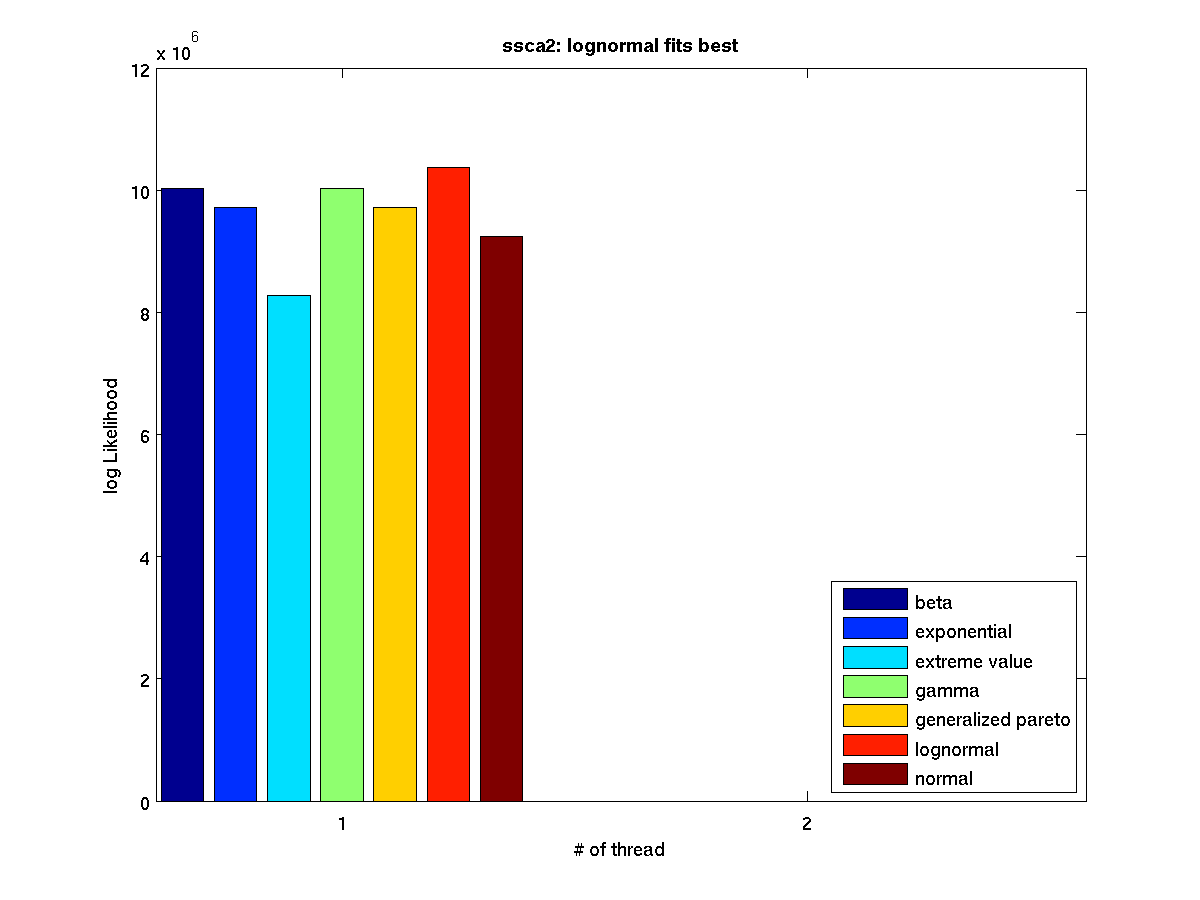
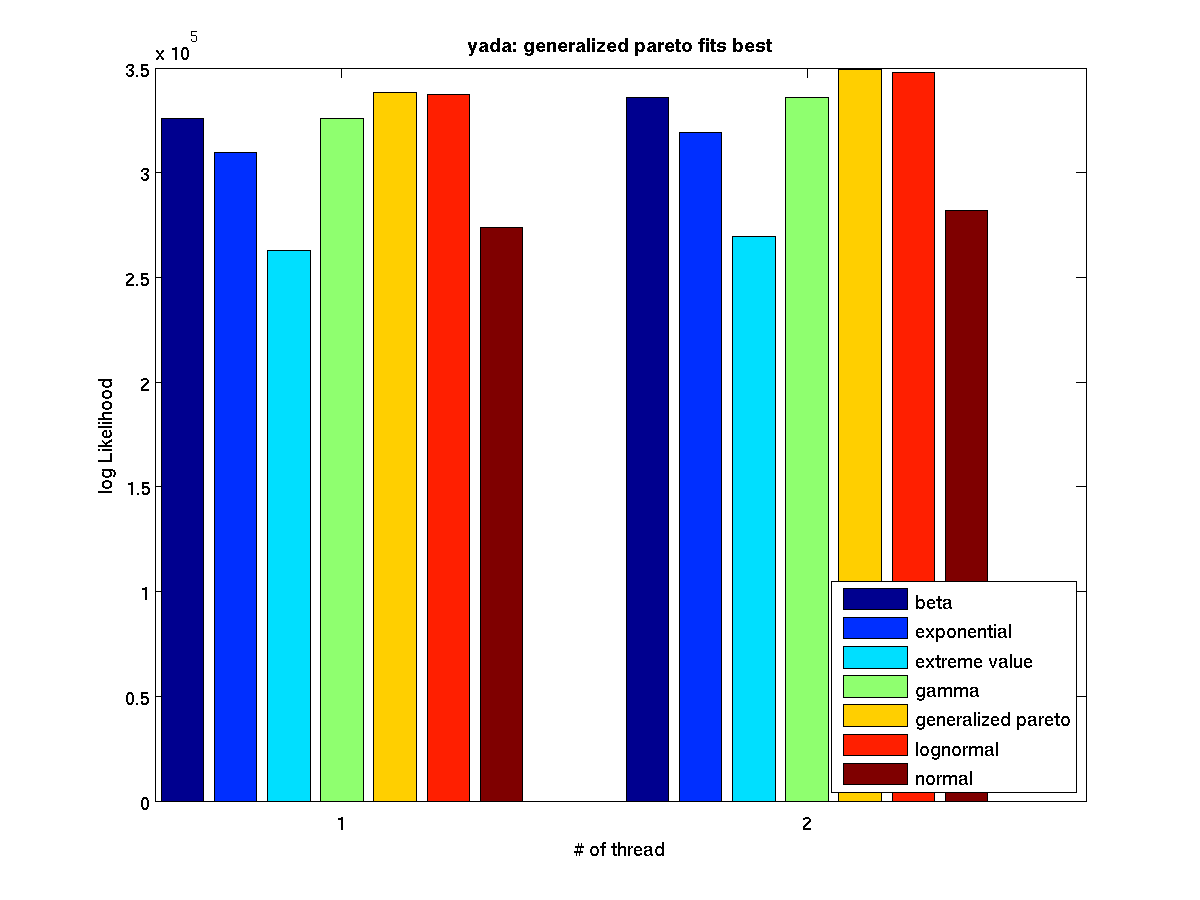
Low contention - Bar graph of log-likelihood valules for 2 threads |
| |
 |
 |
 |
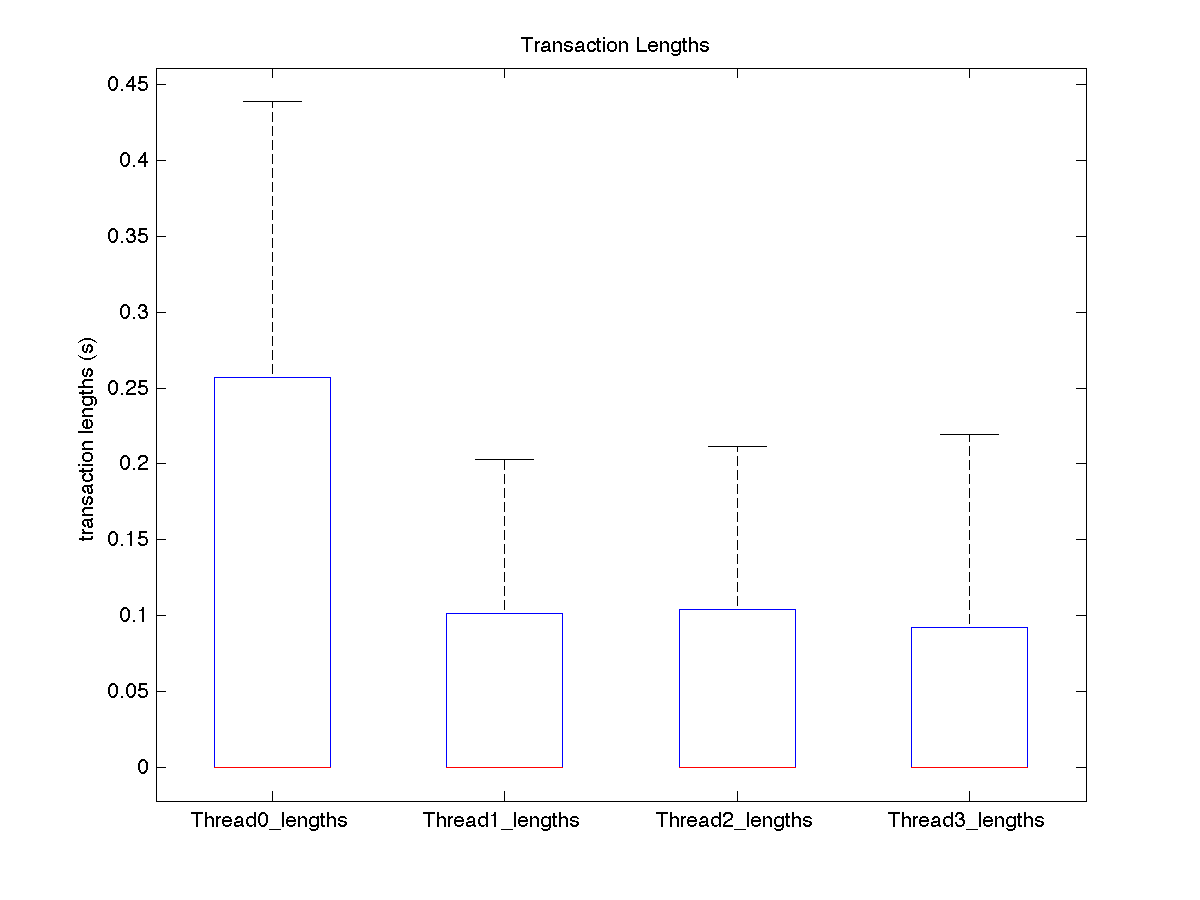
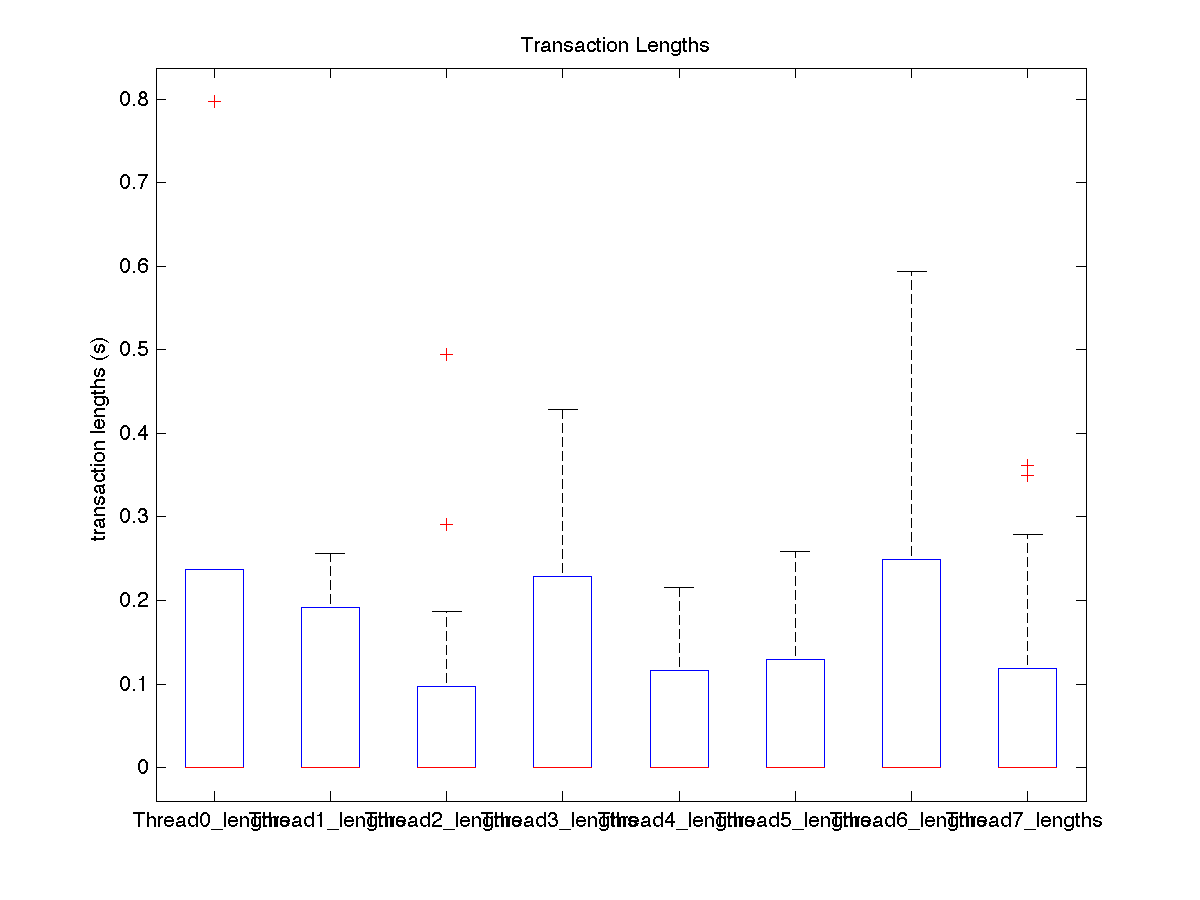
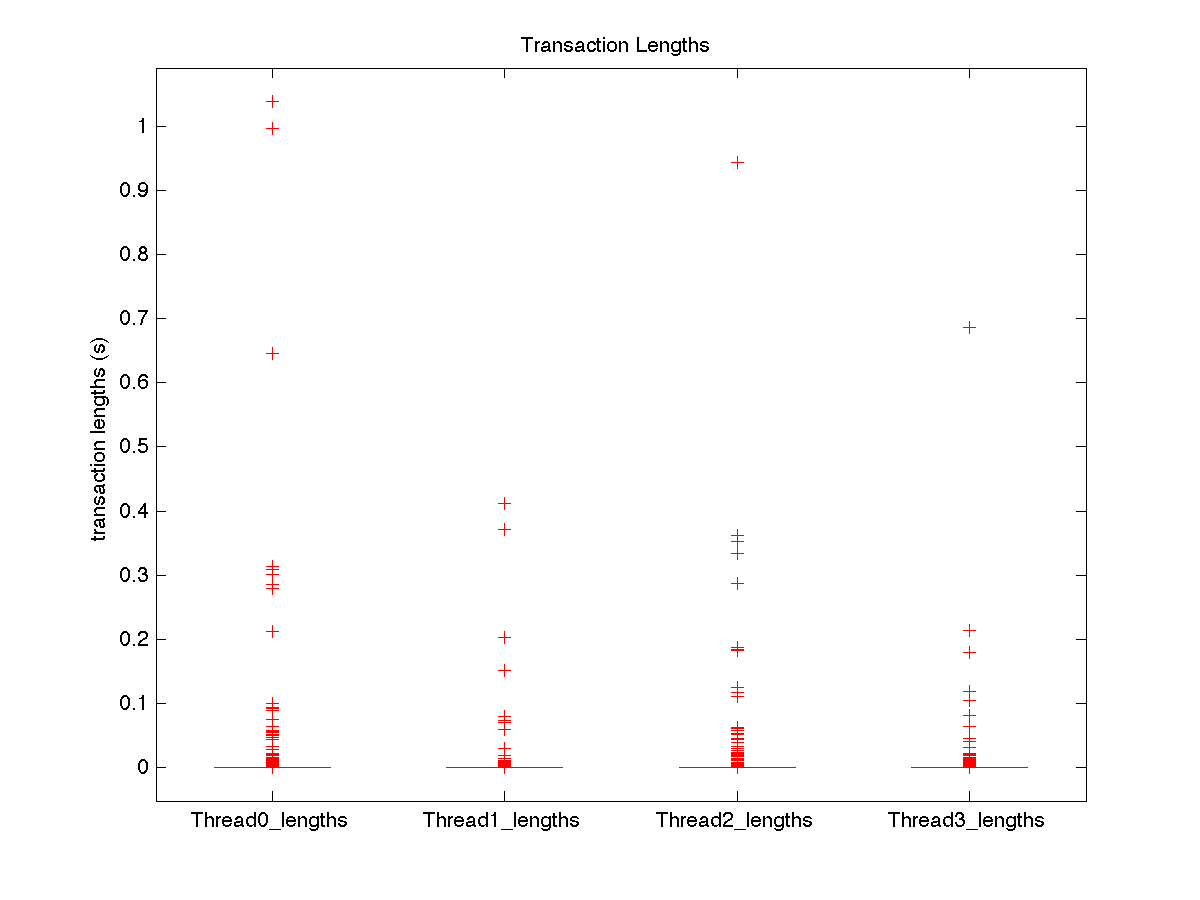
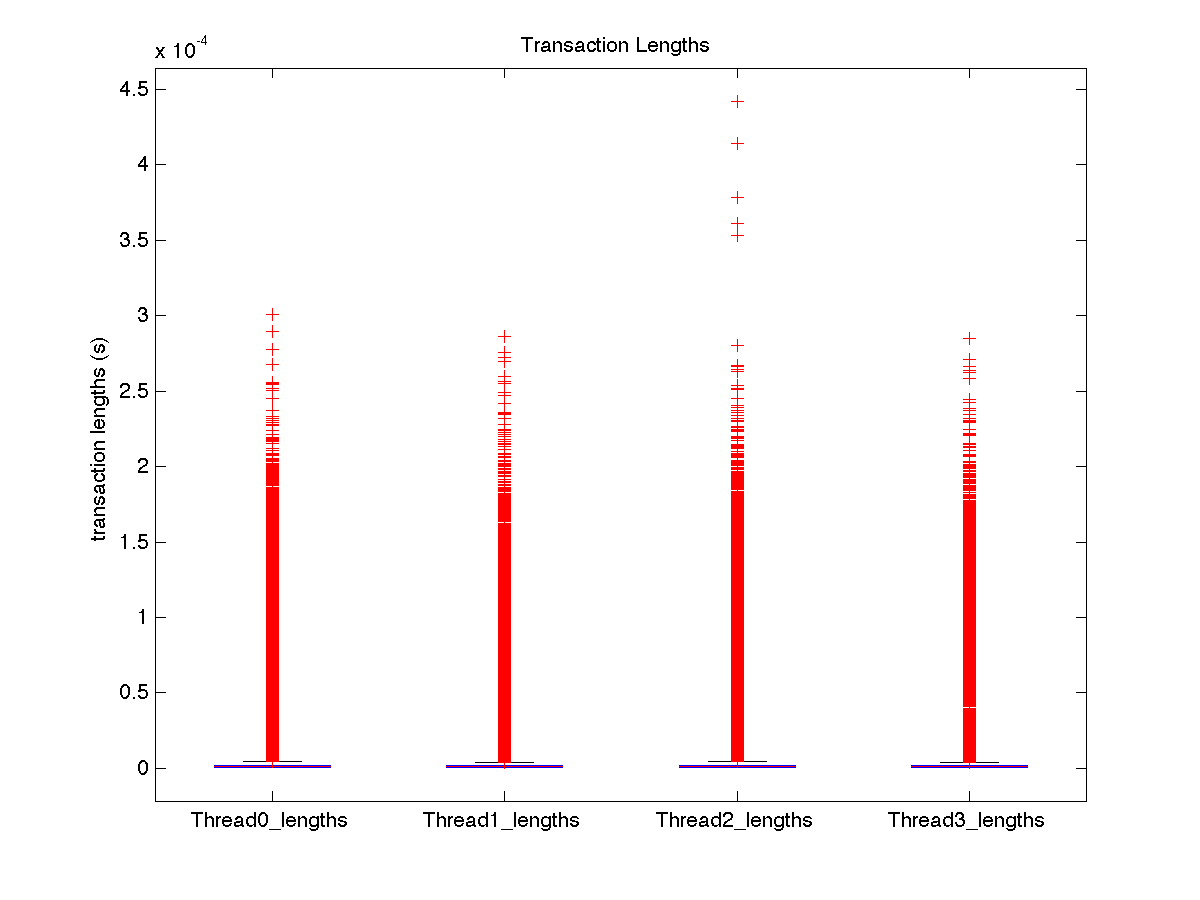
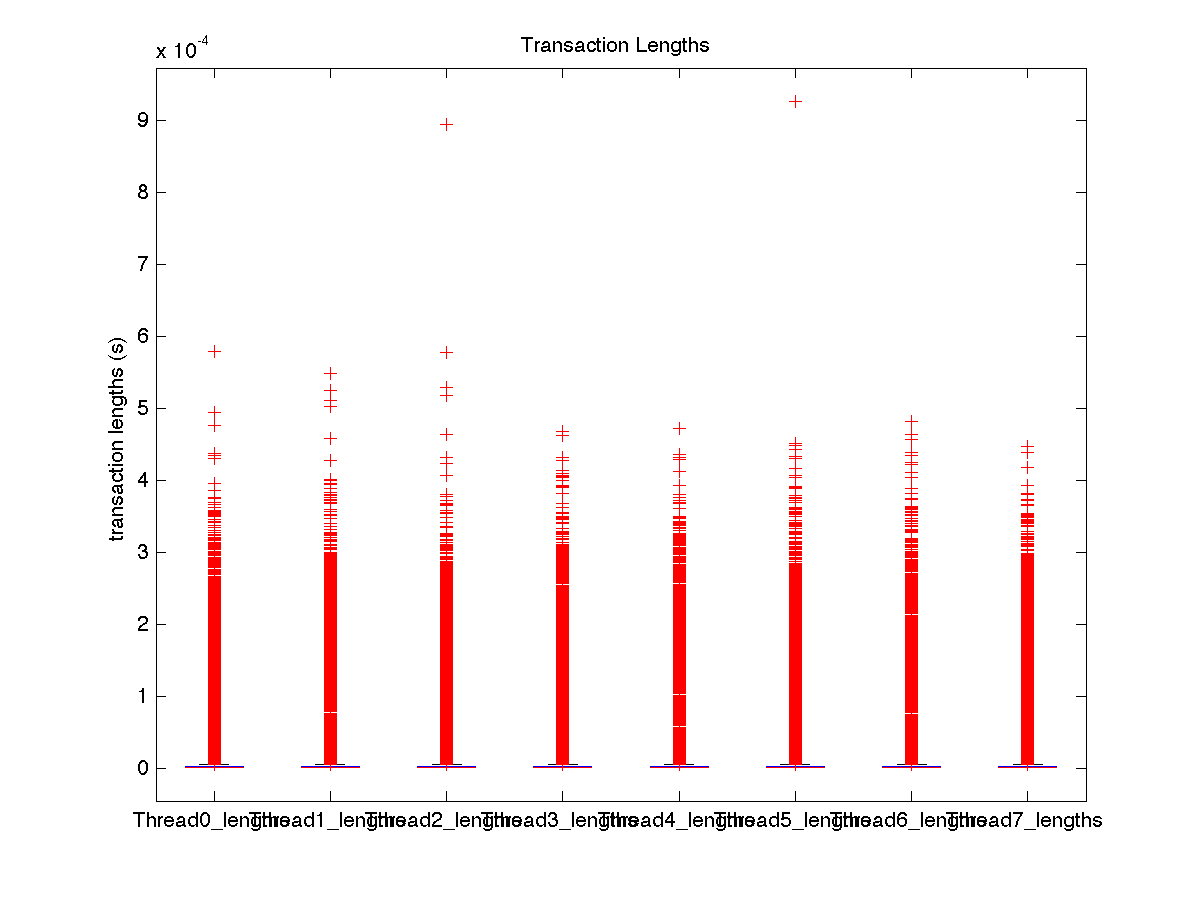
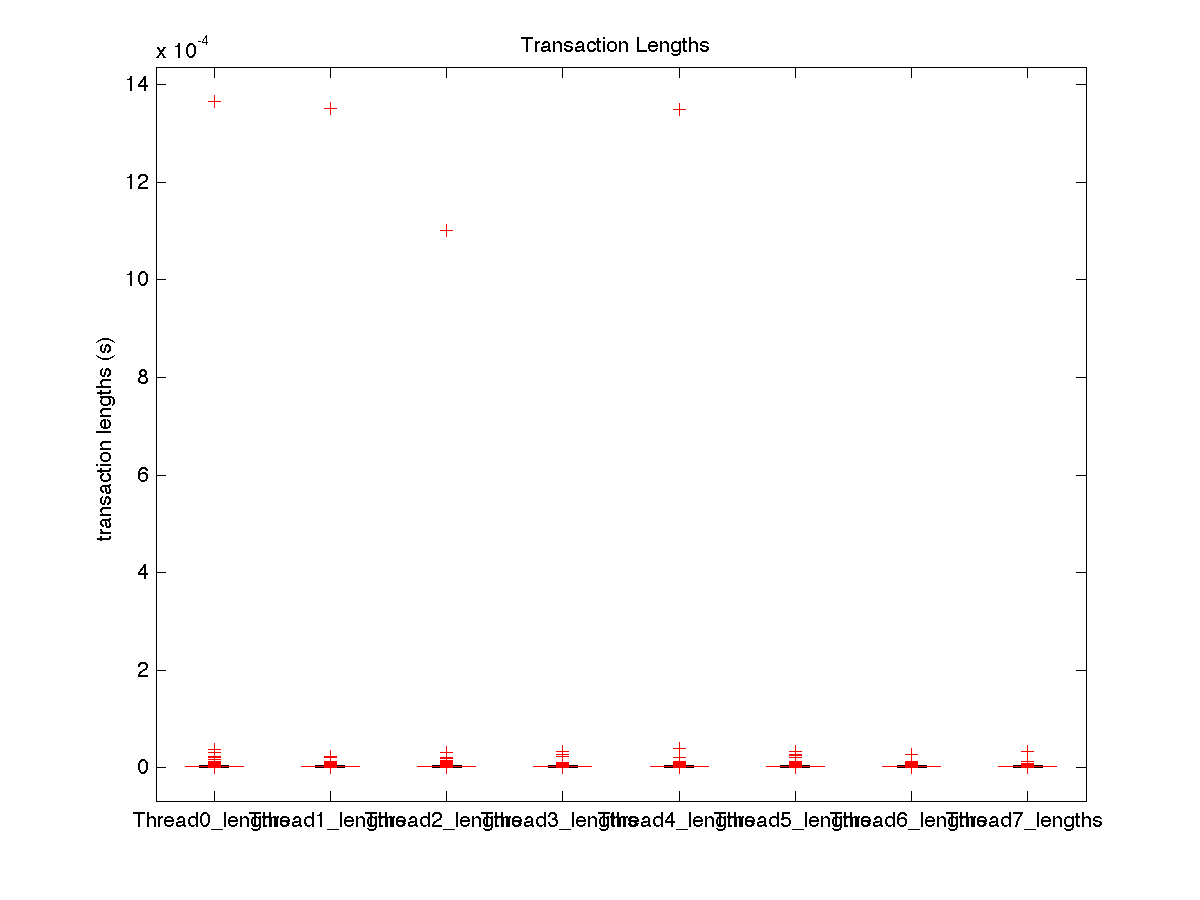
| Low contention - Boxplot of entire distribution for 4 threads |
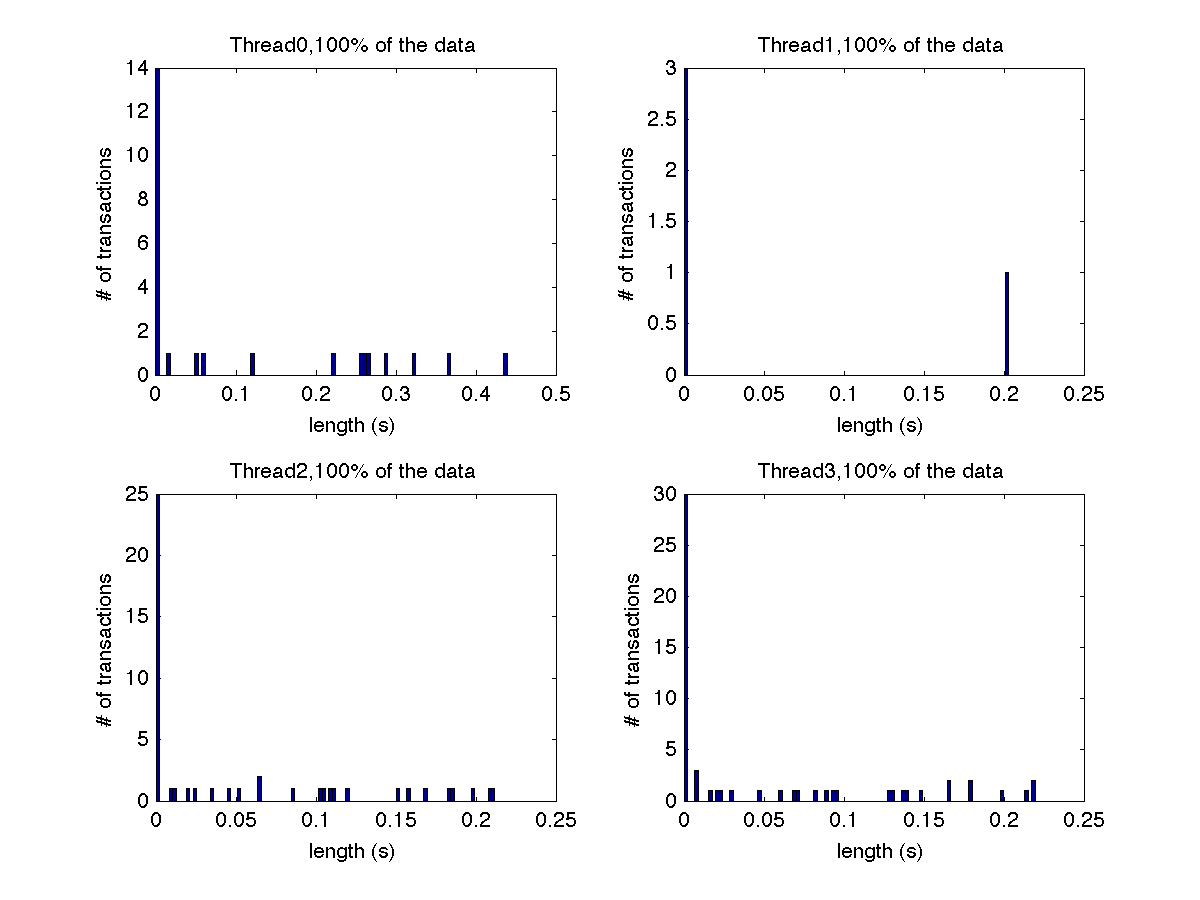
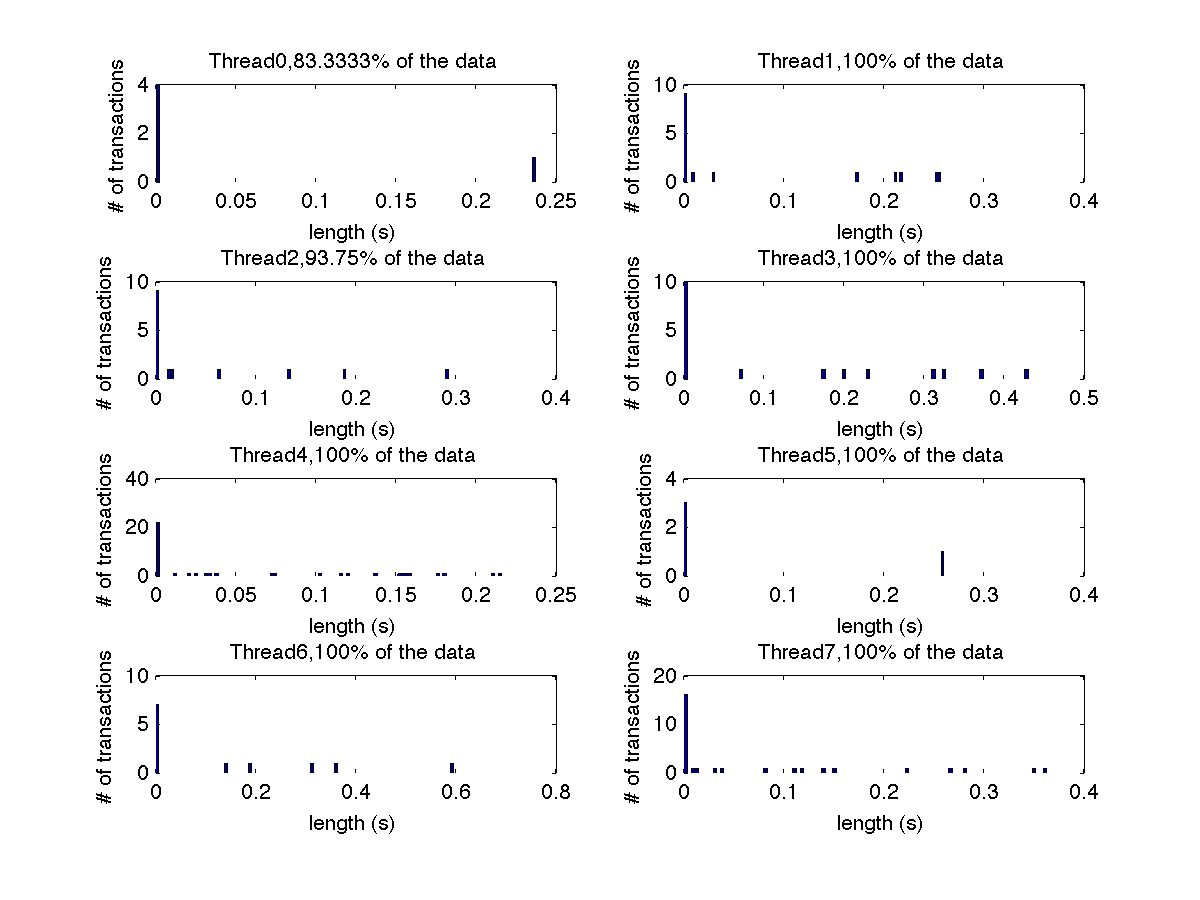
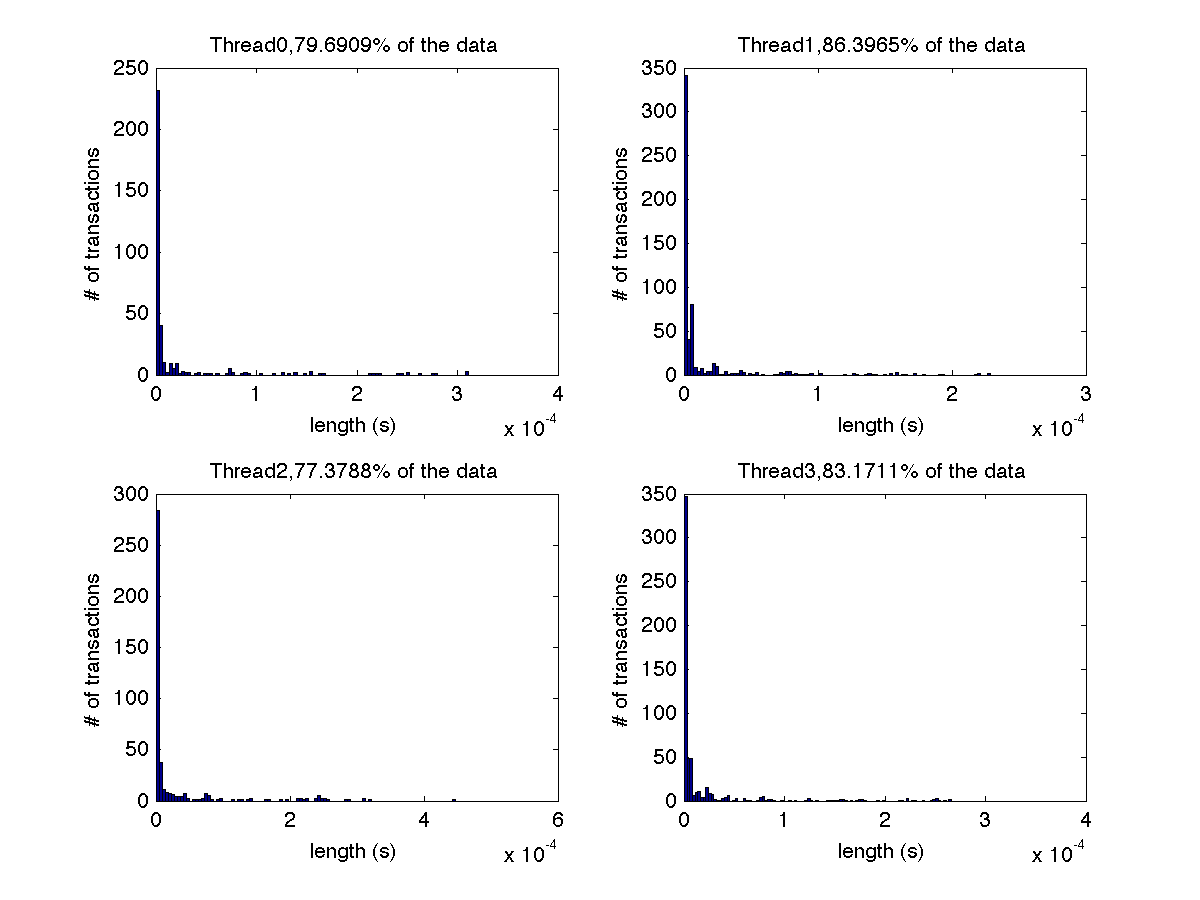
Low contention - Histogram showing majority lengths of transactions for 4 threads (exact percentages in title of graph) |
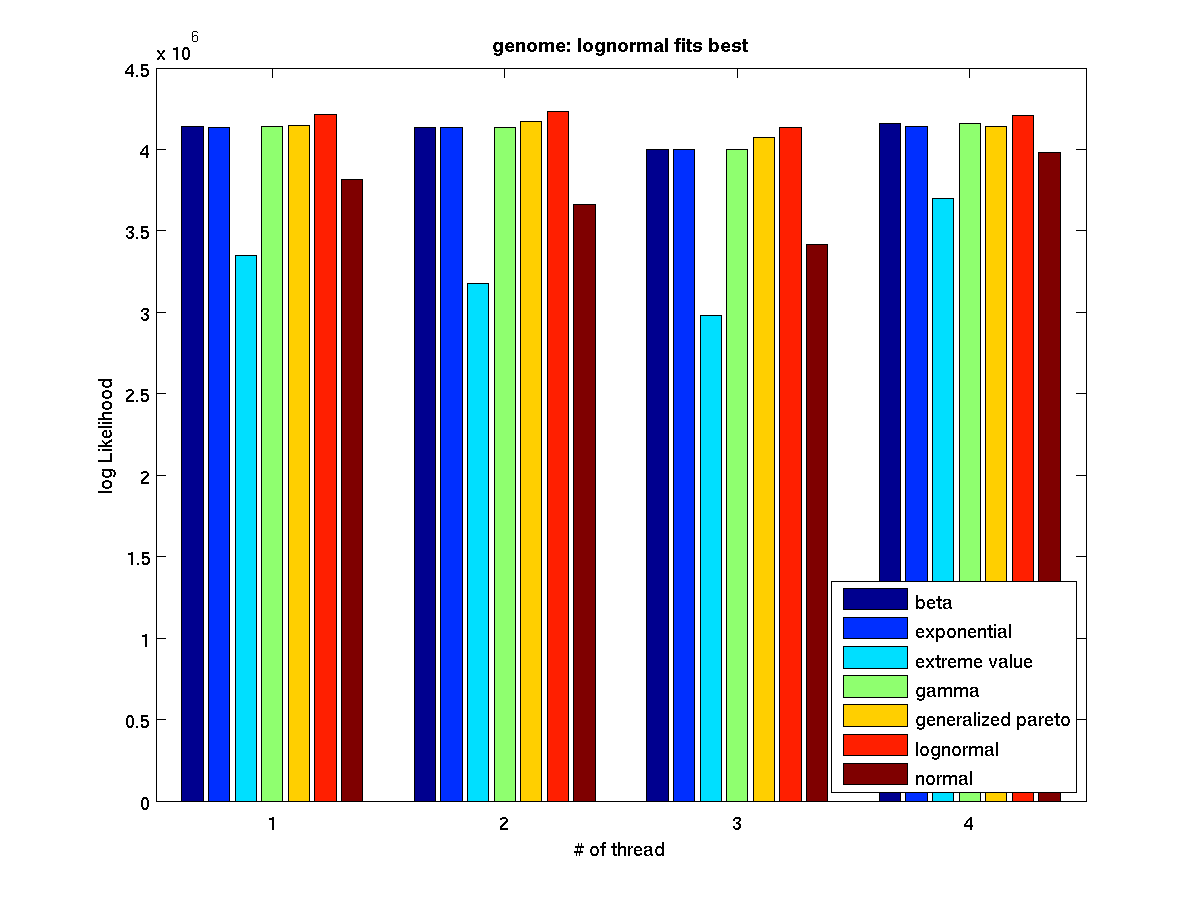
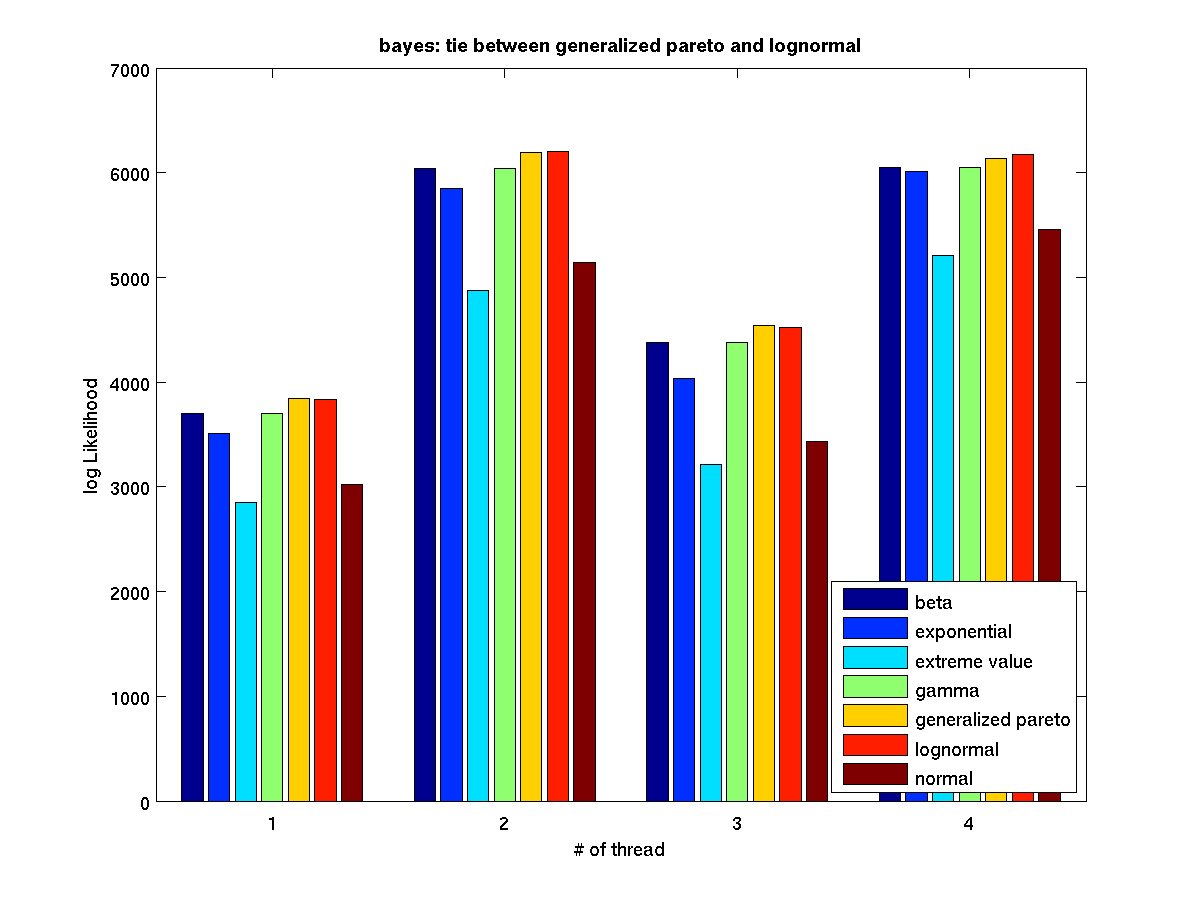
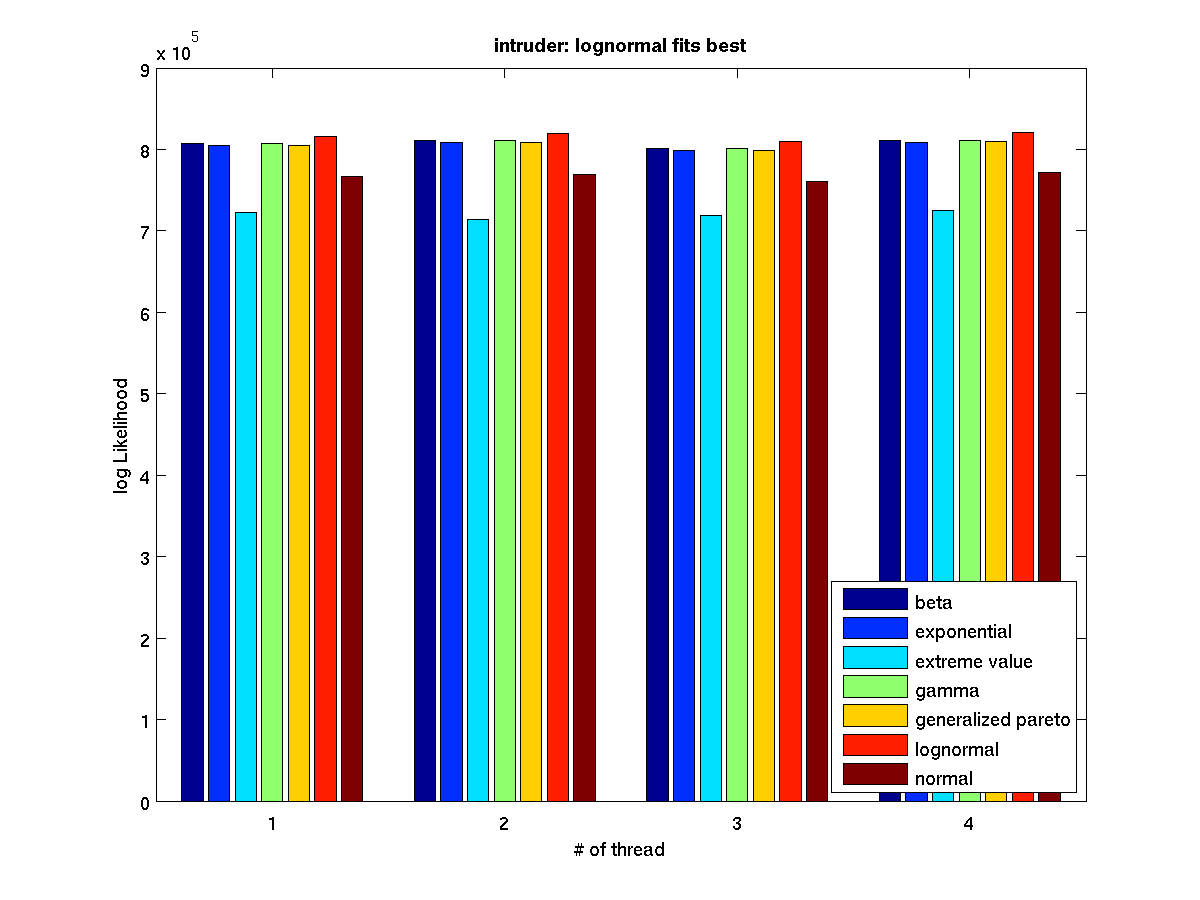
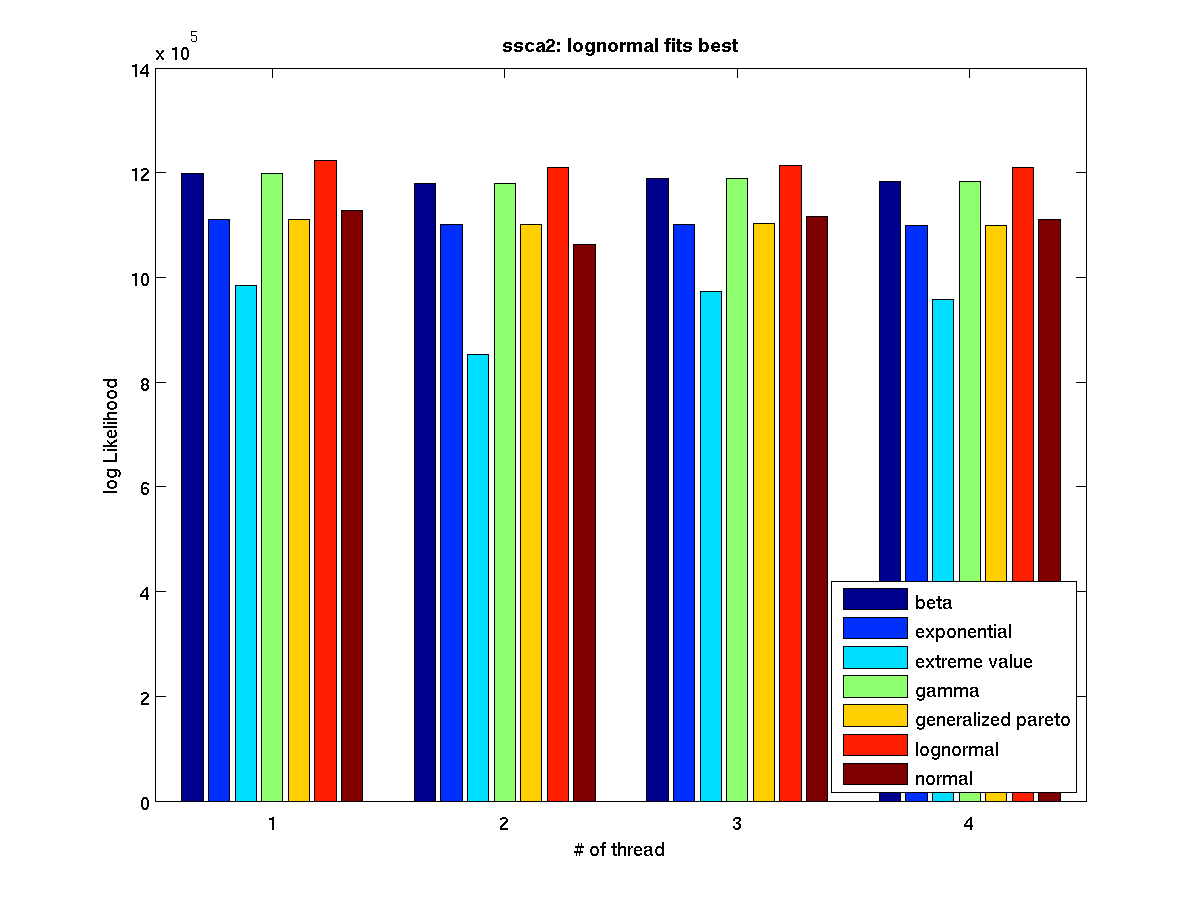
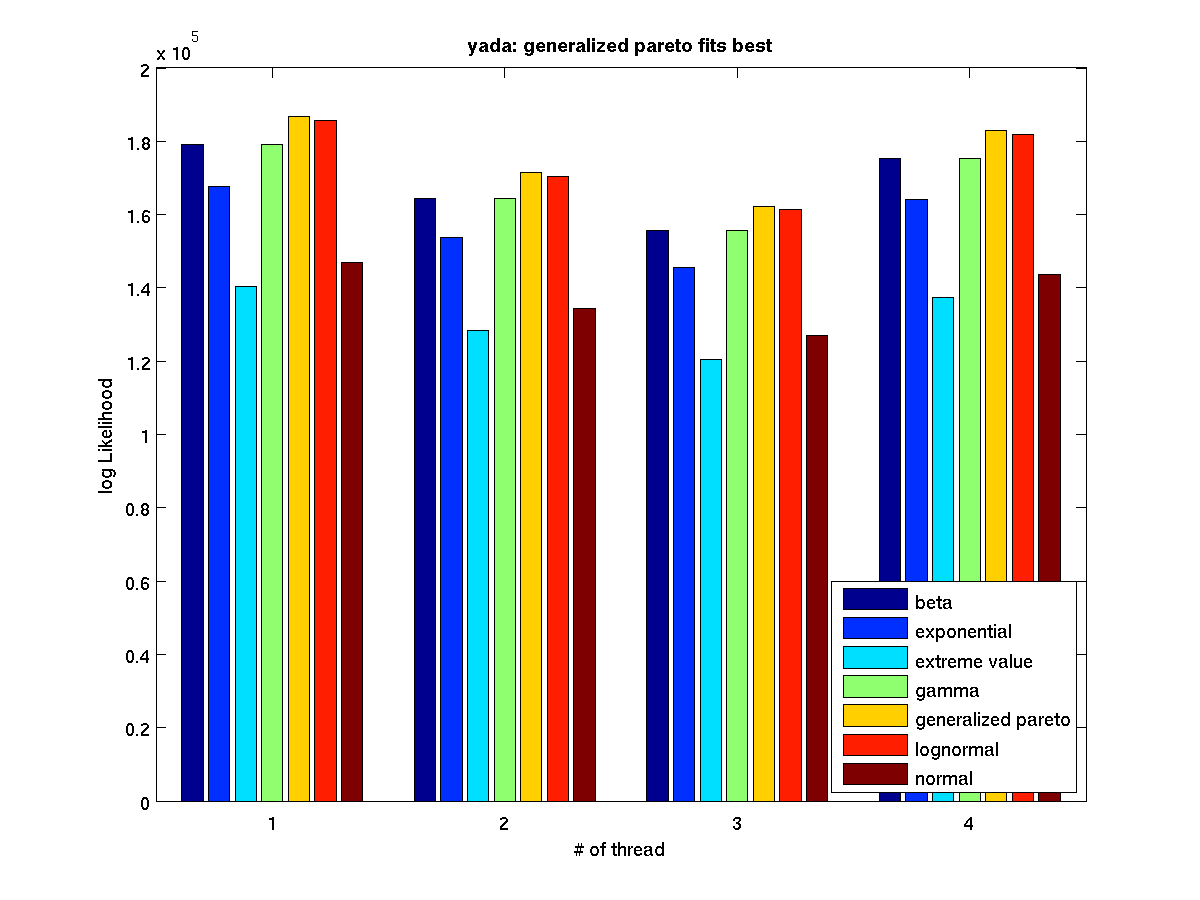
Low contention - Bar graph of log-likelihood valules for 4 threads |
| |
 |
 |
 |
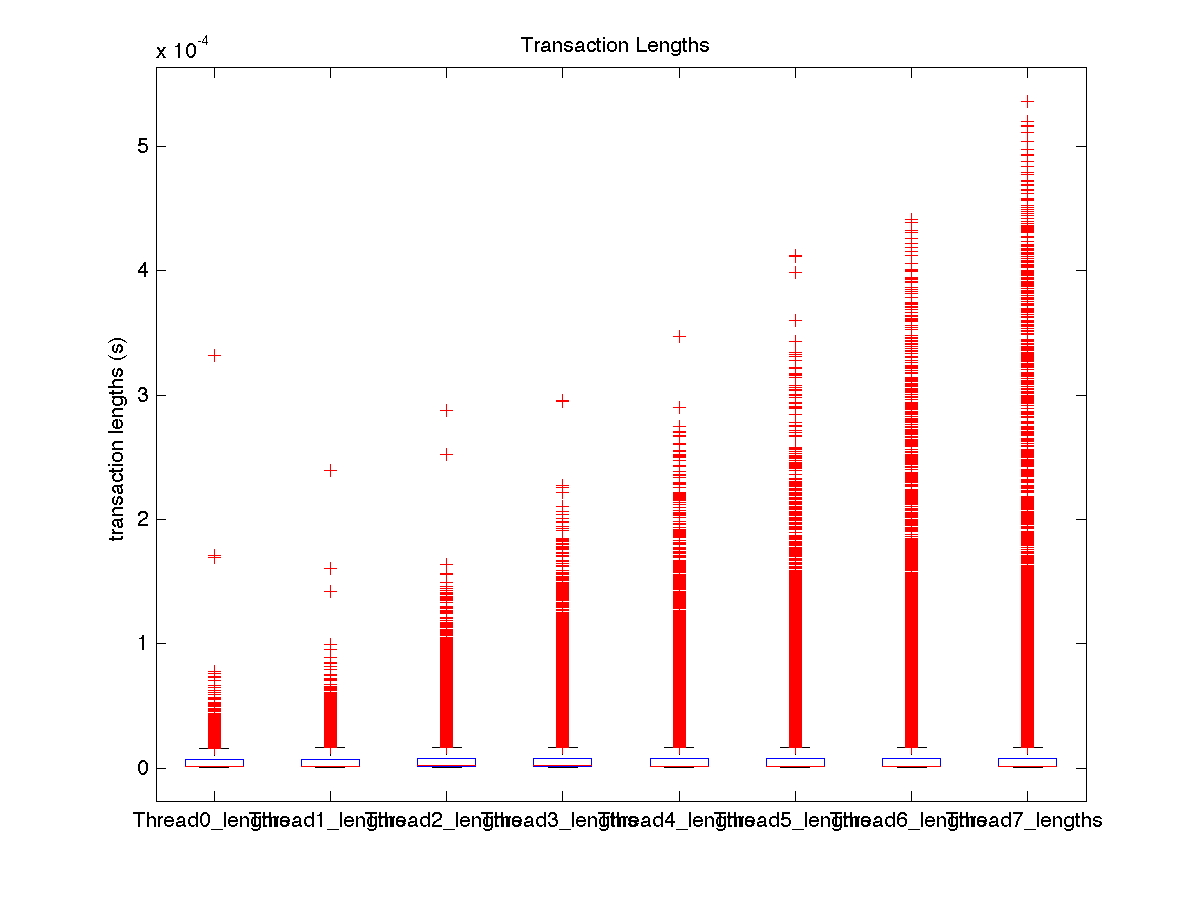
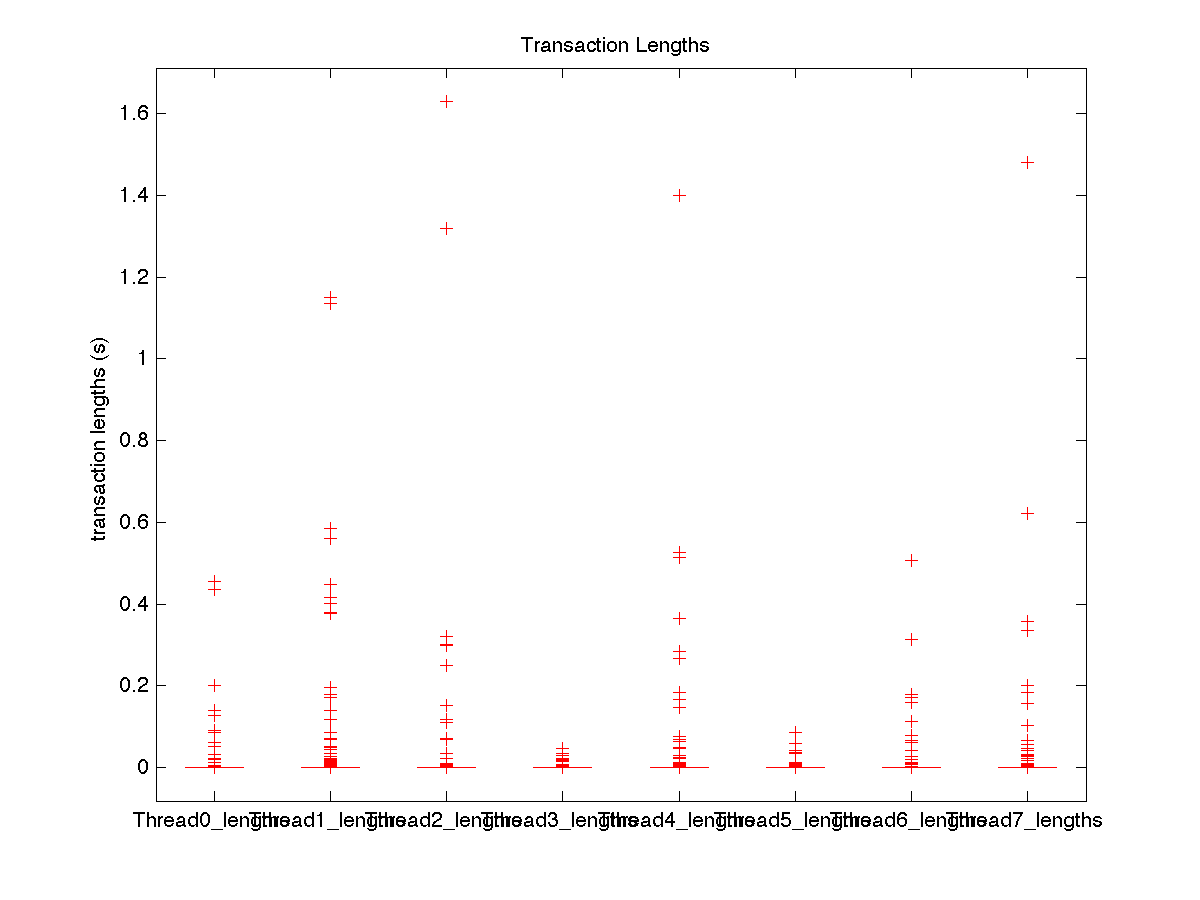
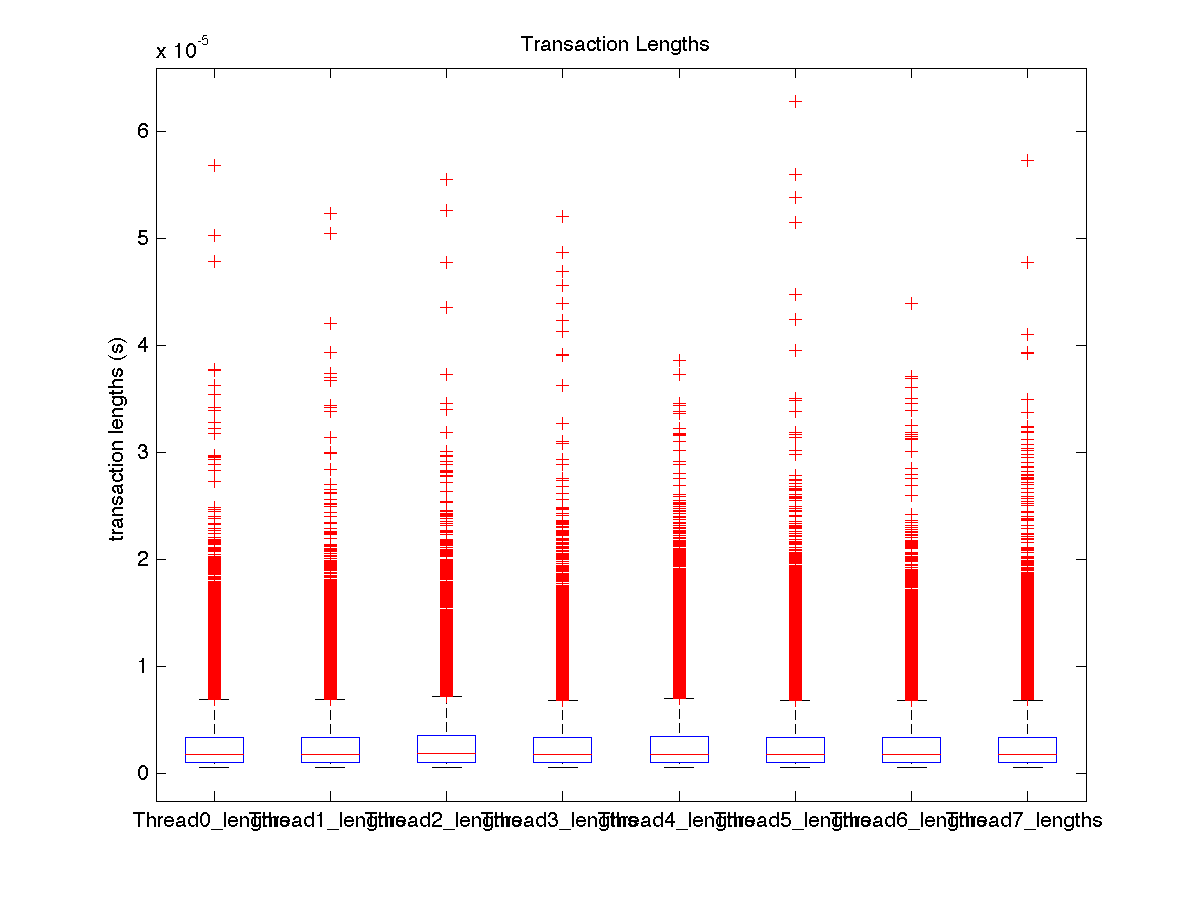
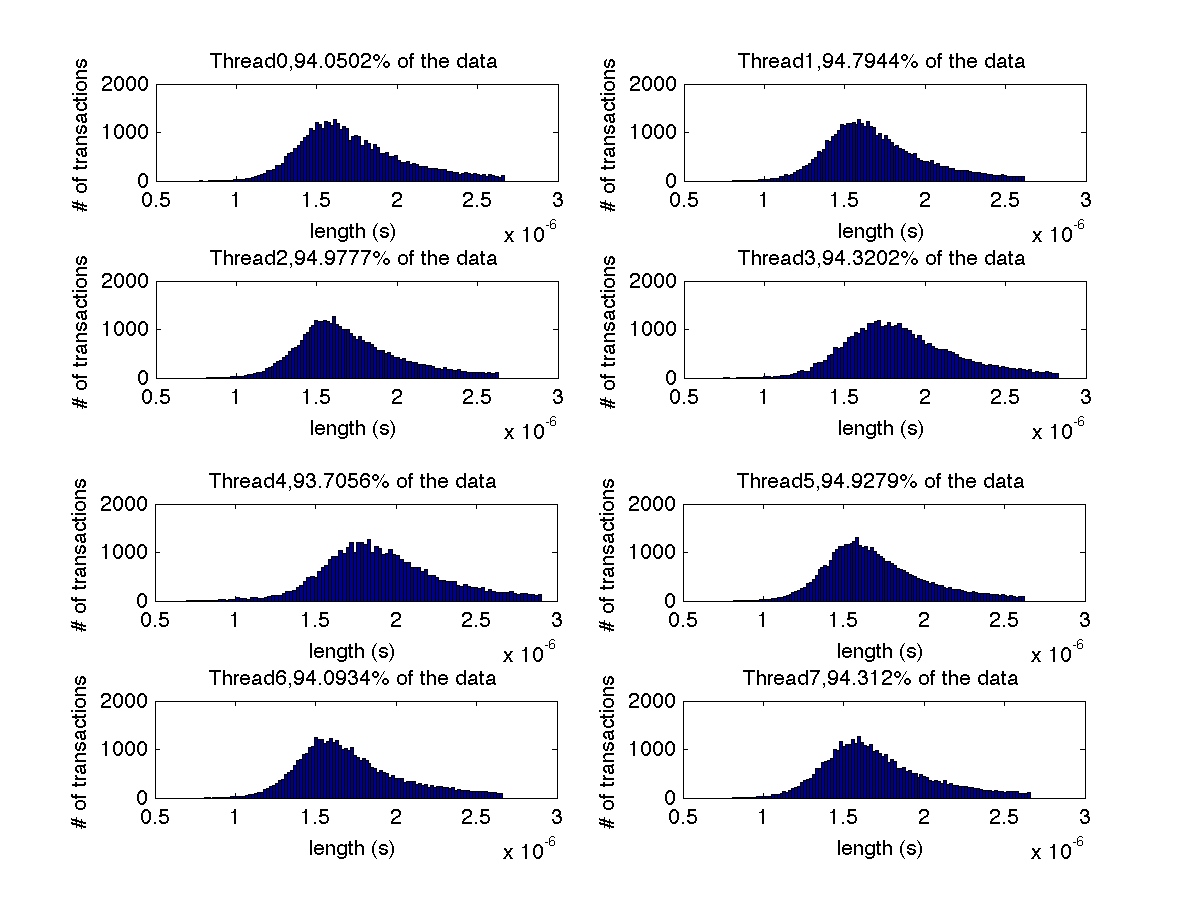
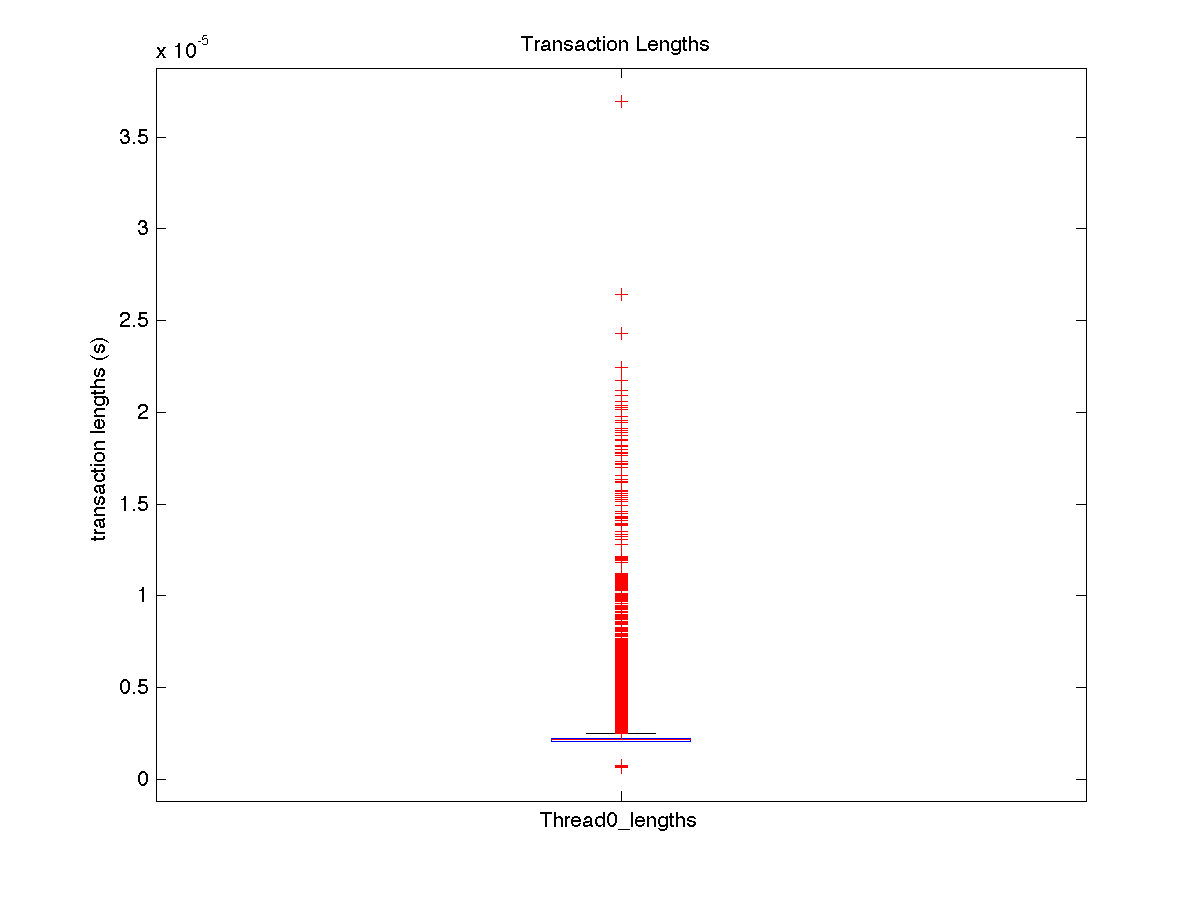
| Low contention - Boxplot of entire distribution for 8 threads |
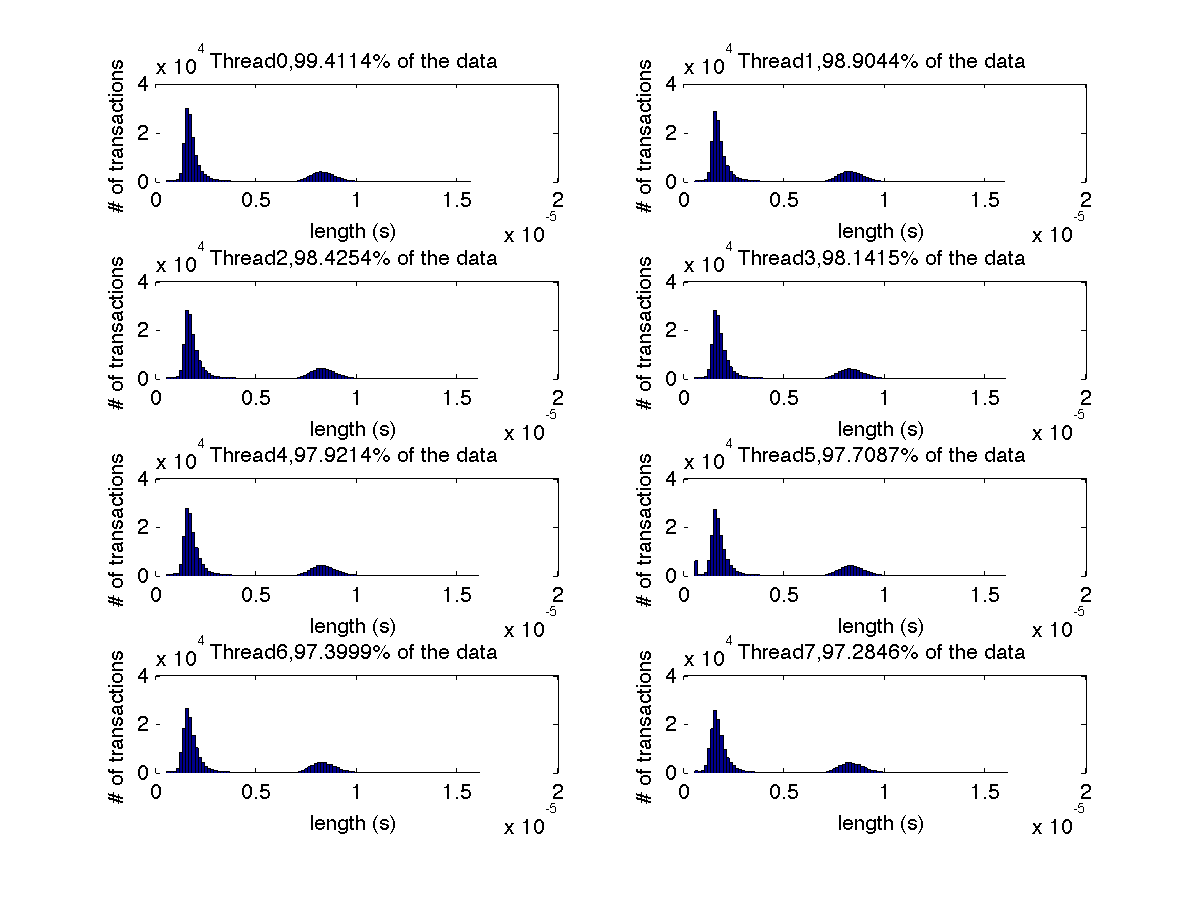
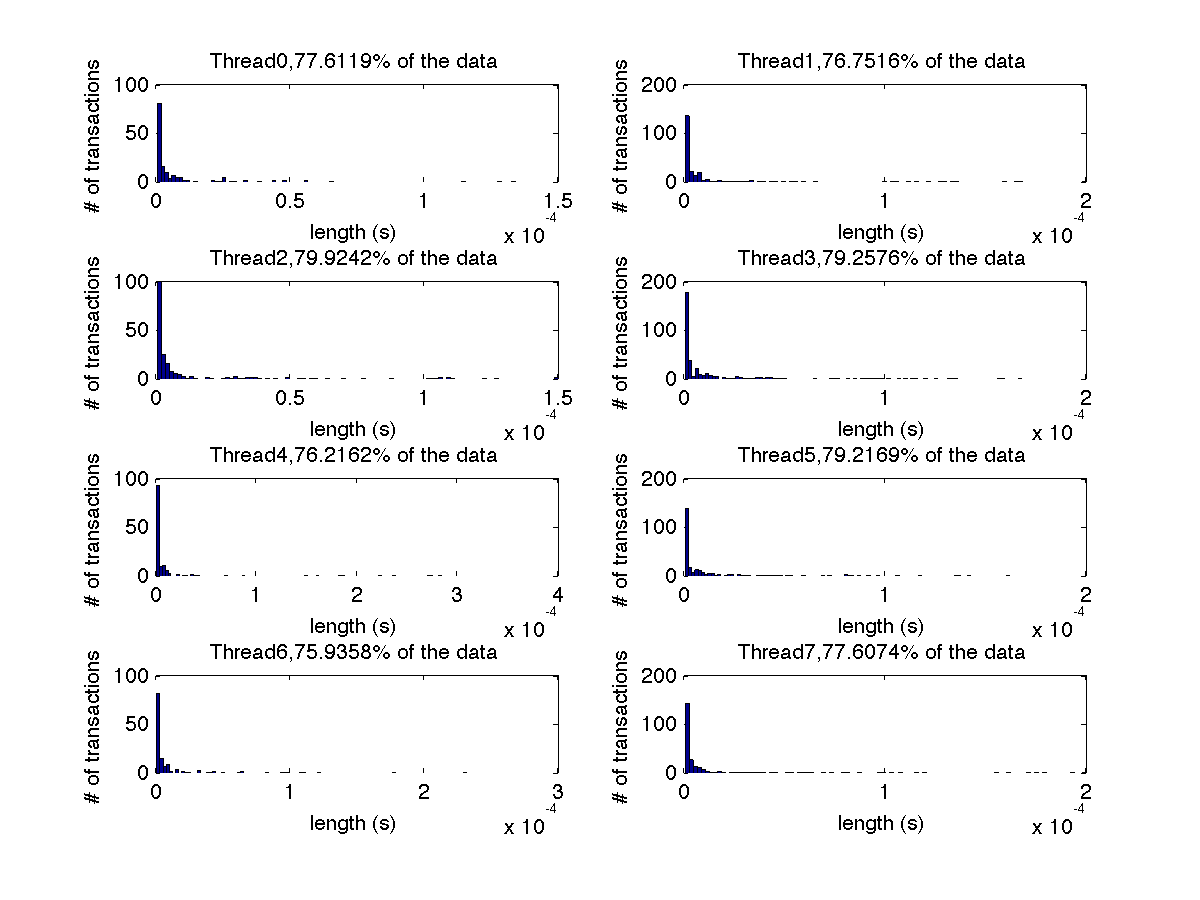
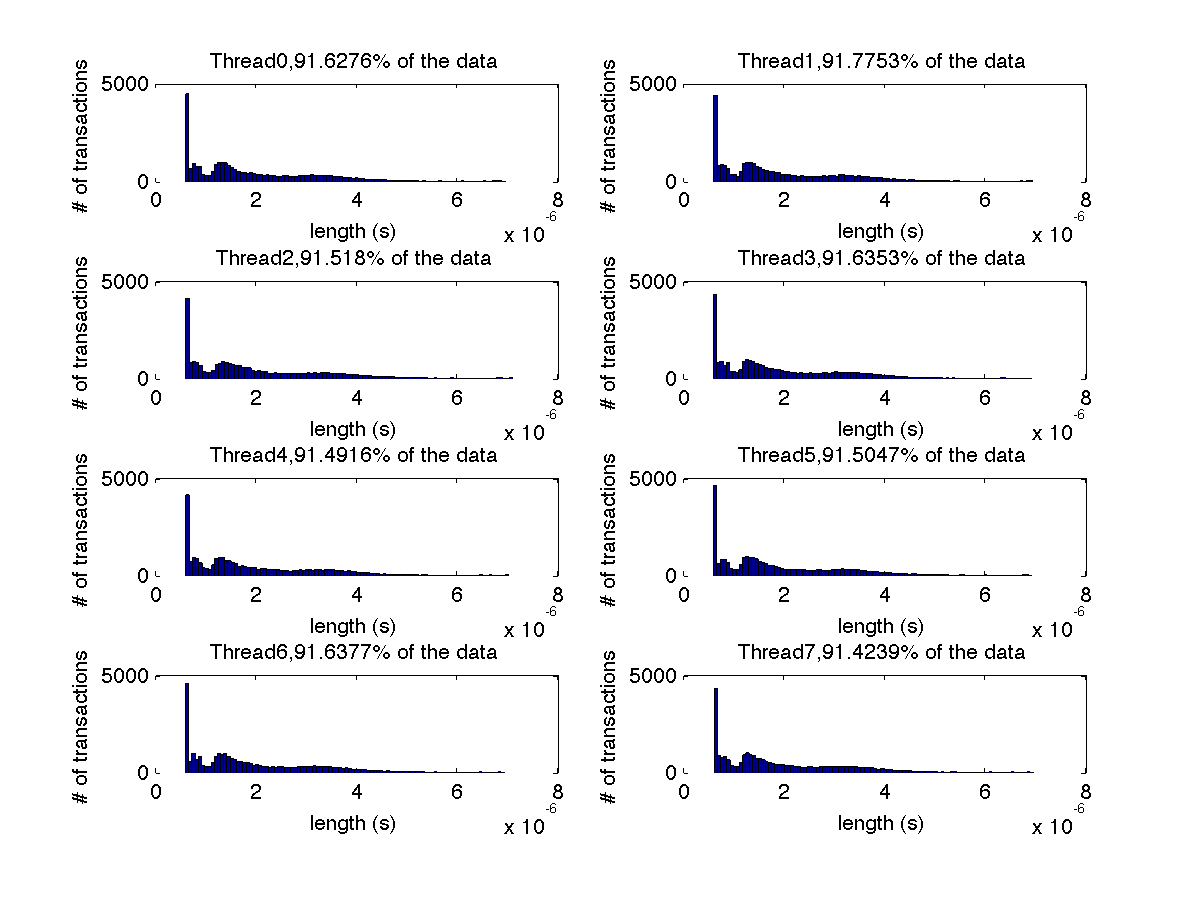
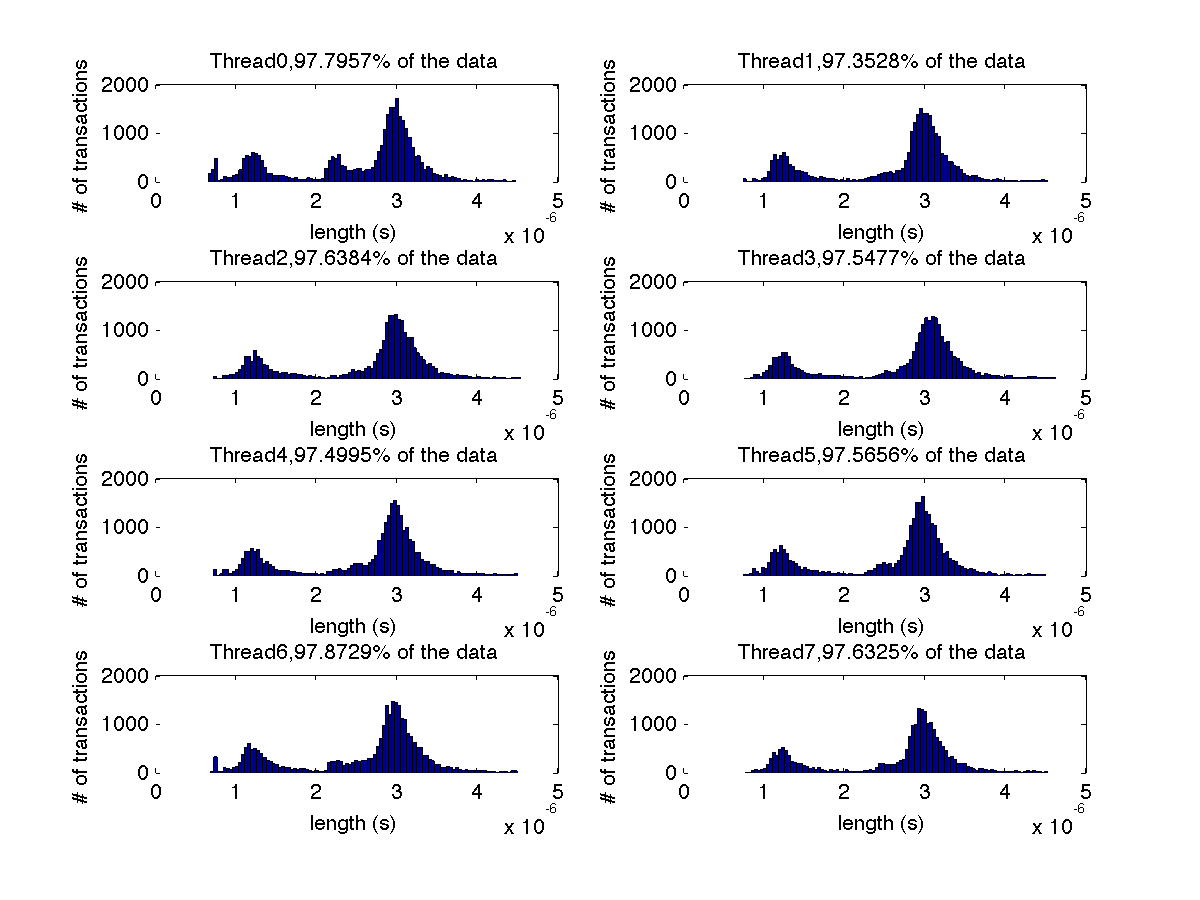
Low contention - Histogram showing majority lengths of transactions for 8 threads (exact percentages in title of graph) |
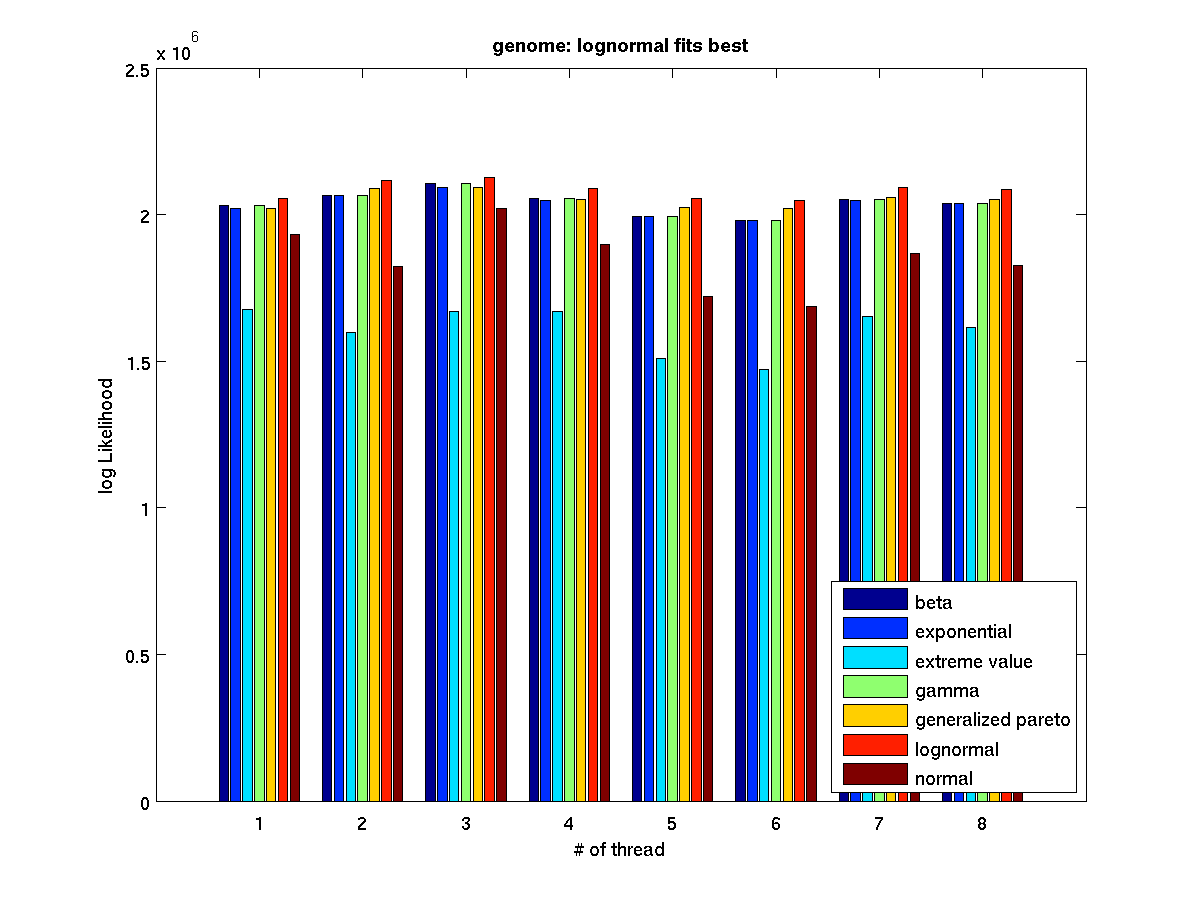
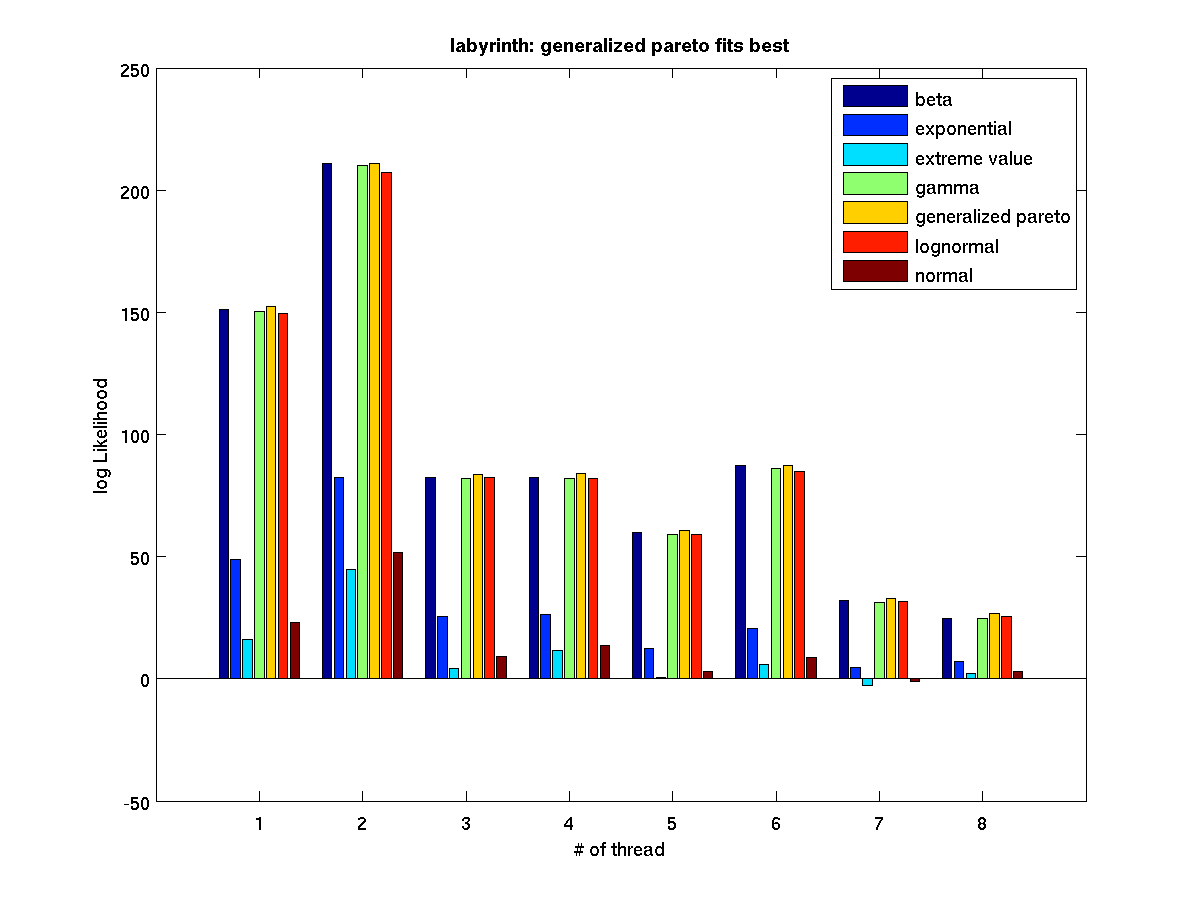
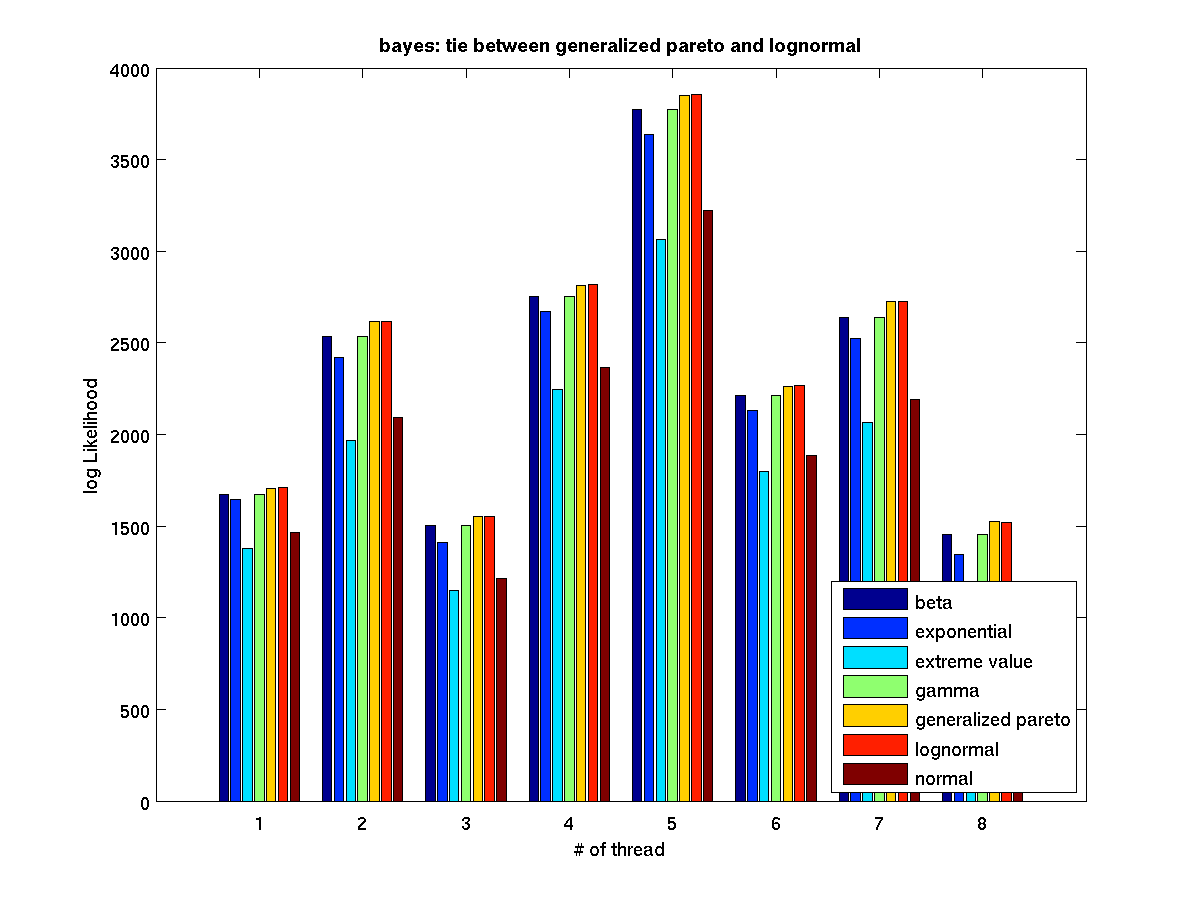
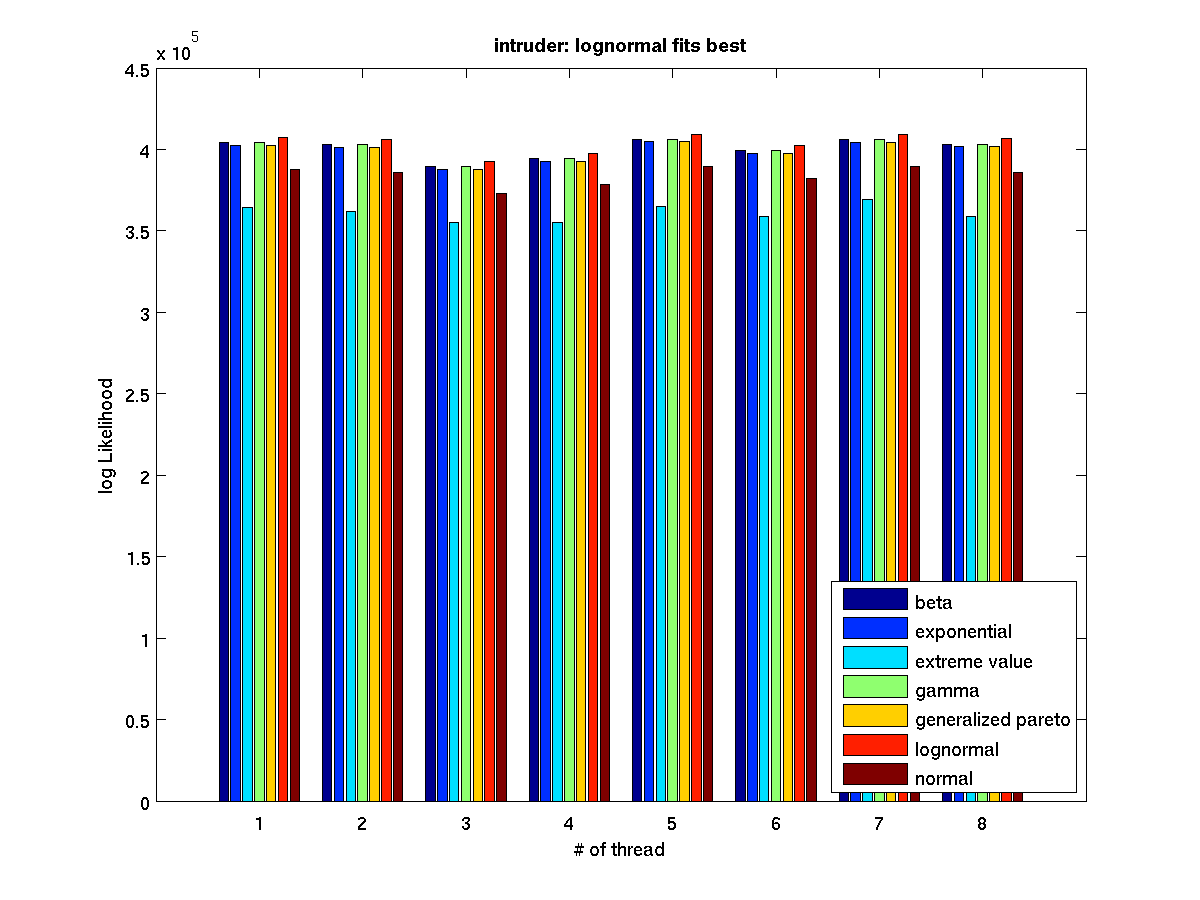
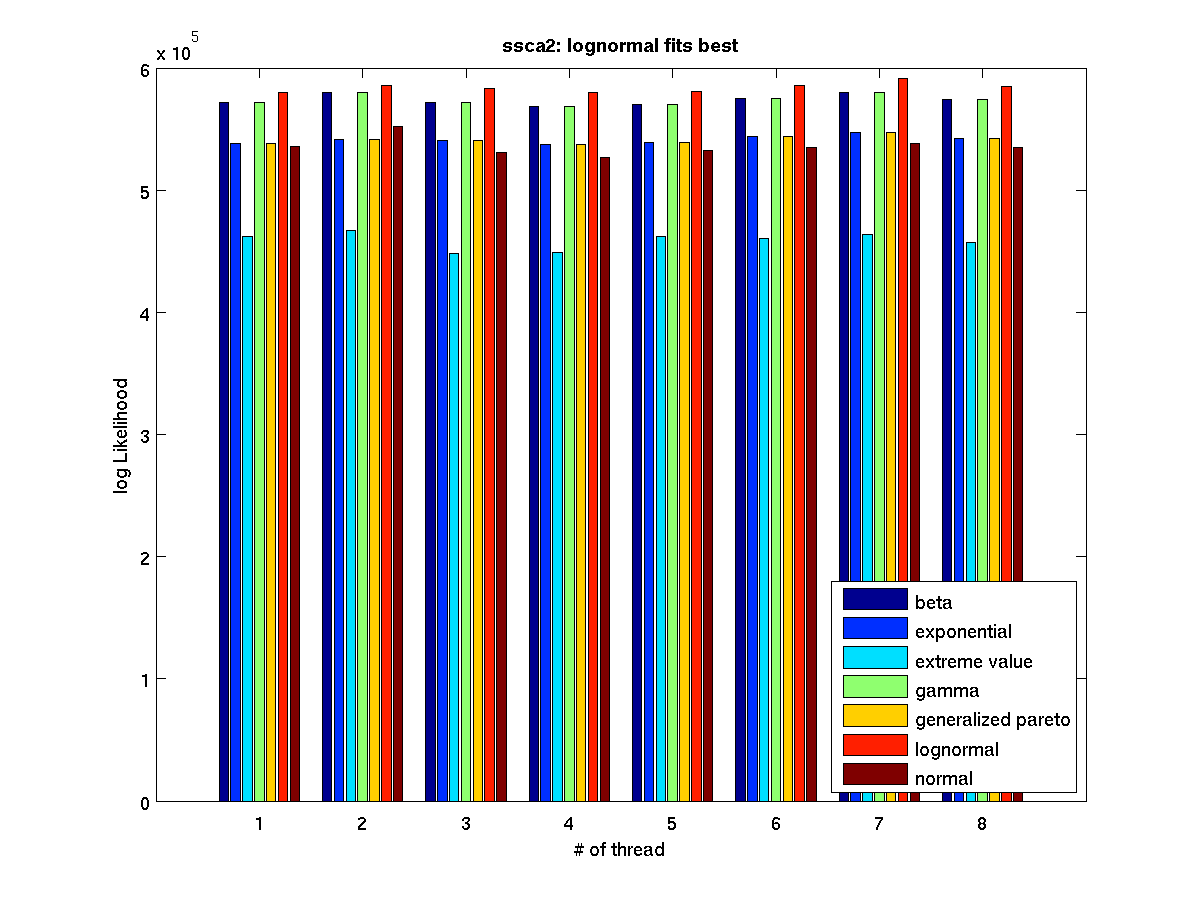
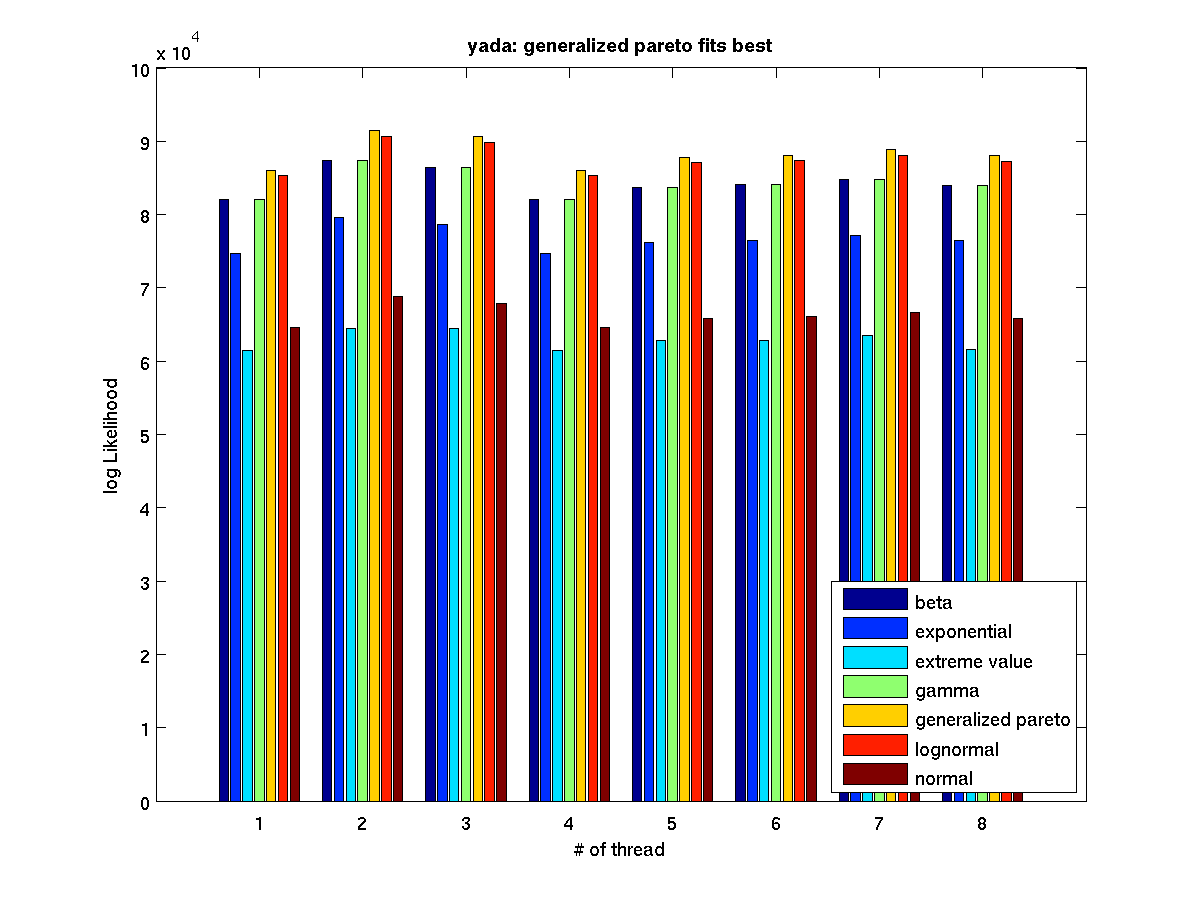
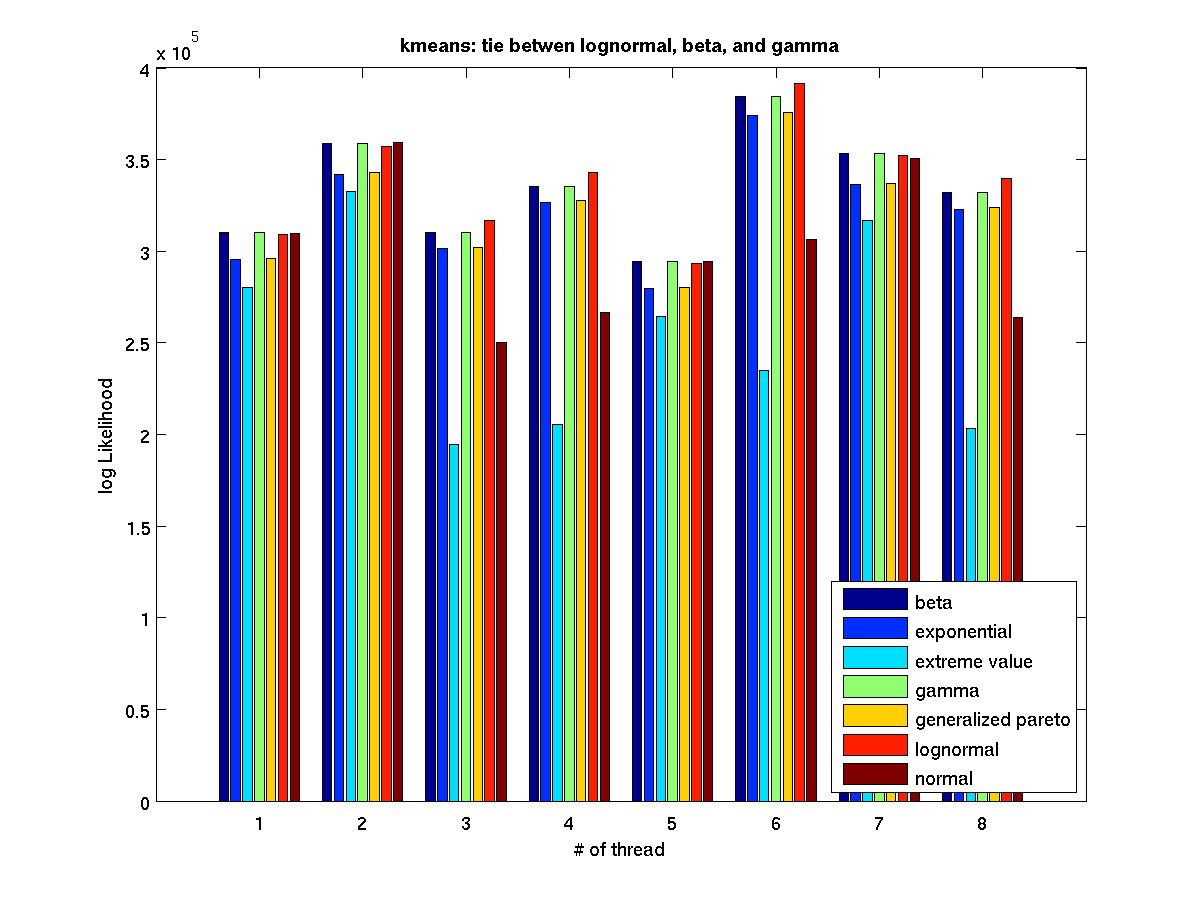
Low contention - Bar graph of log-likelihood valules for 8 threads |
| |
 |
 |
 |
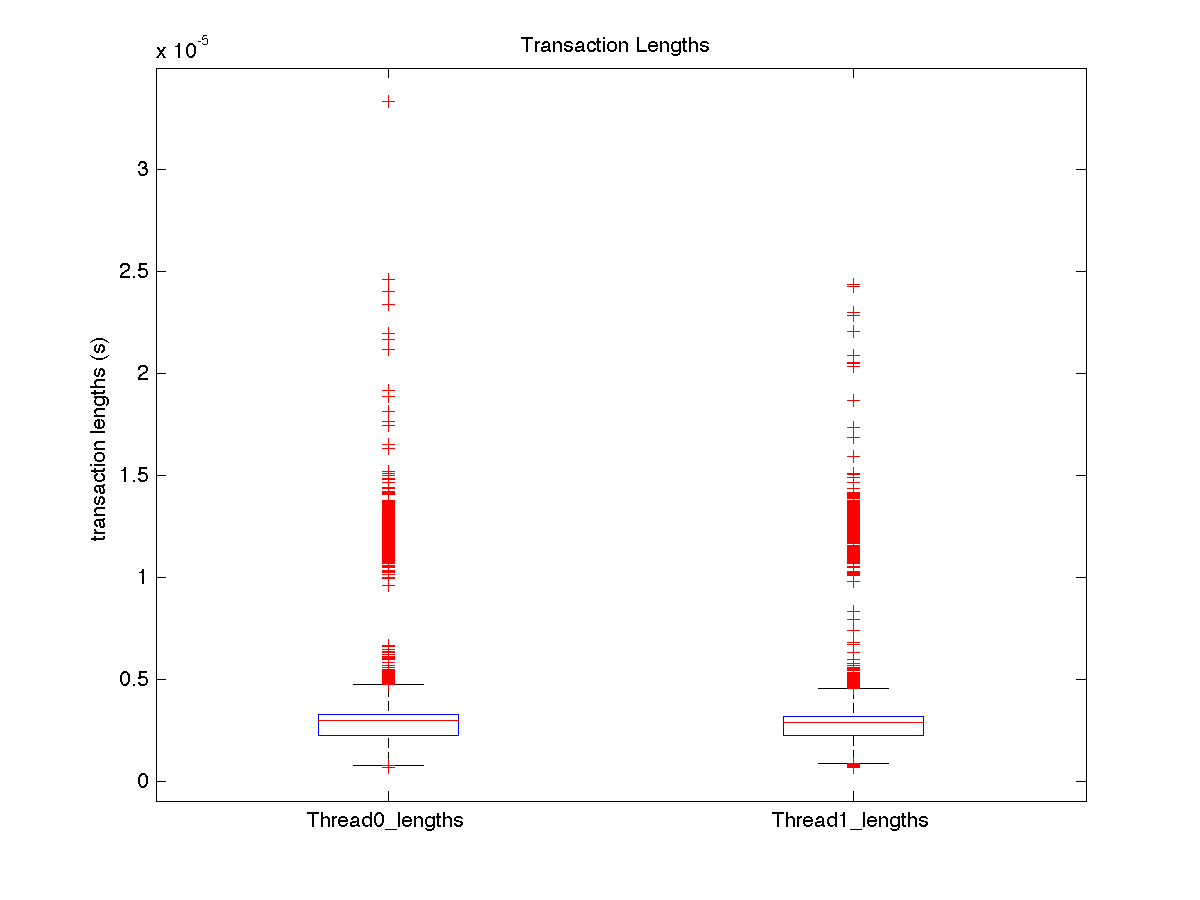
| High contention - Boxplot of entire distribution for 1 thread |
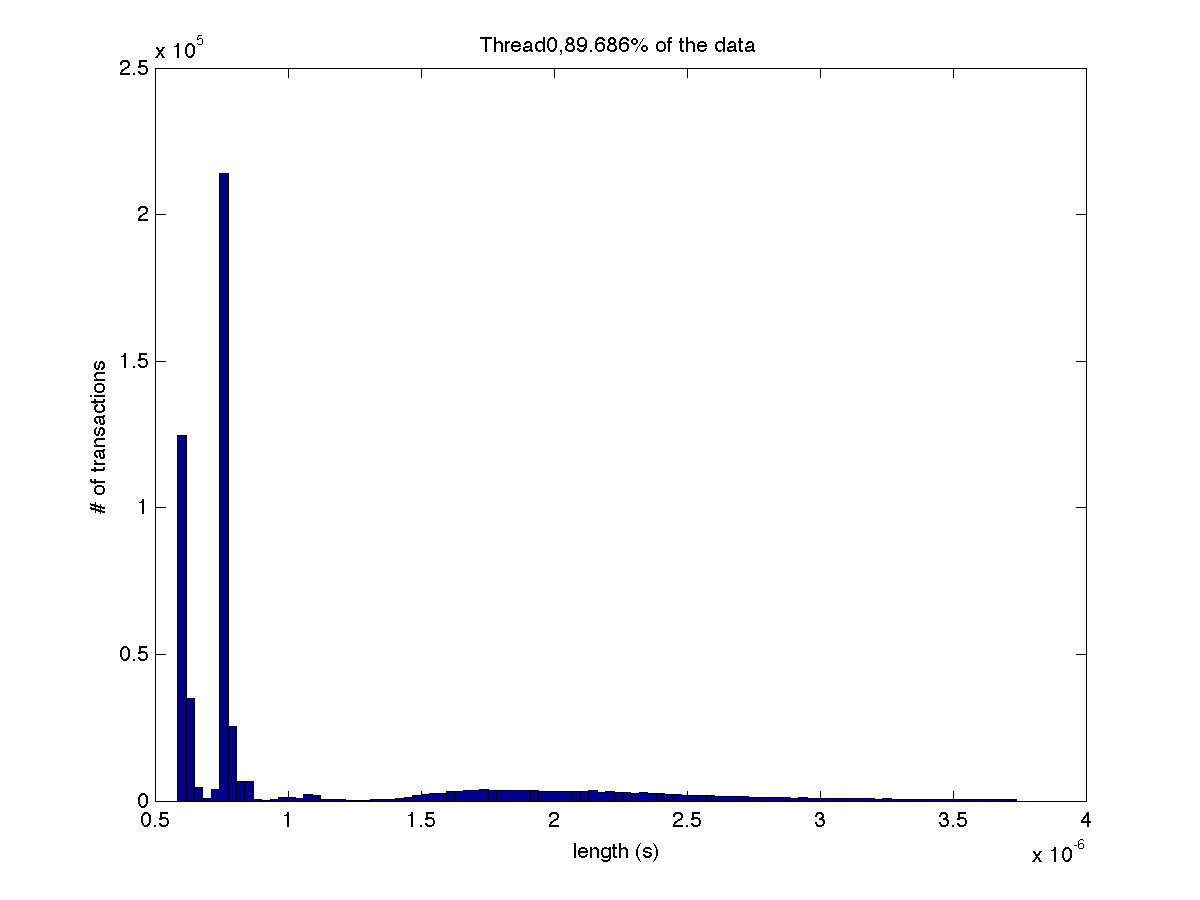
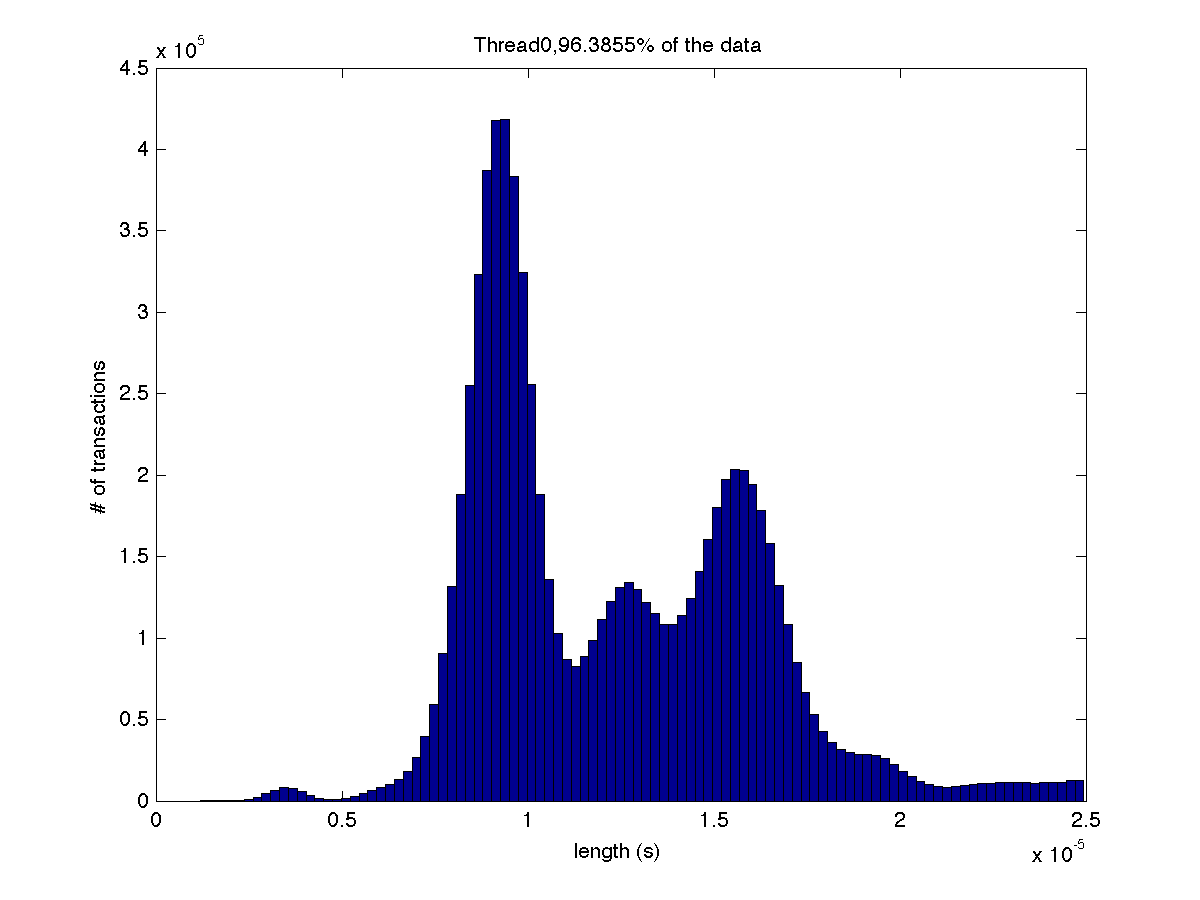
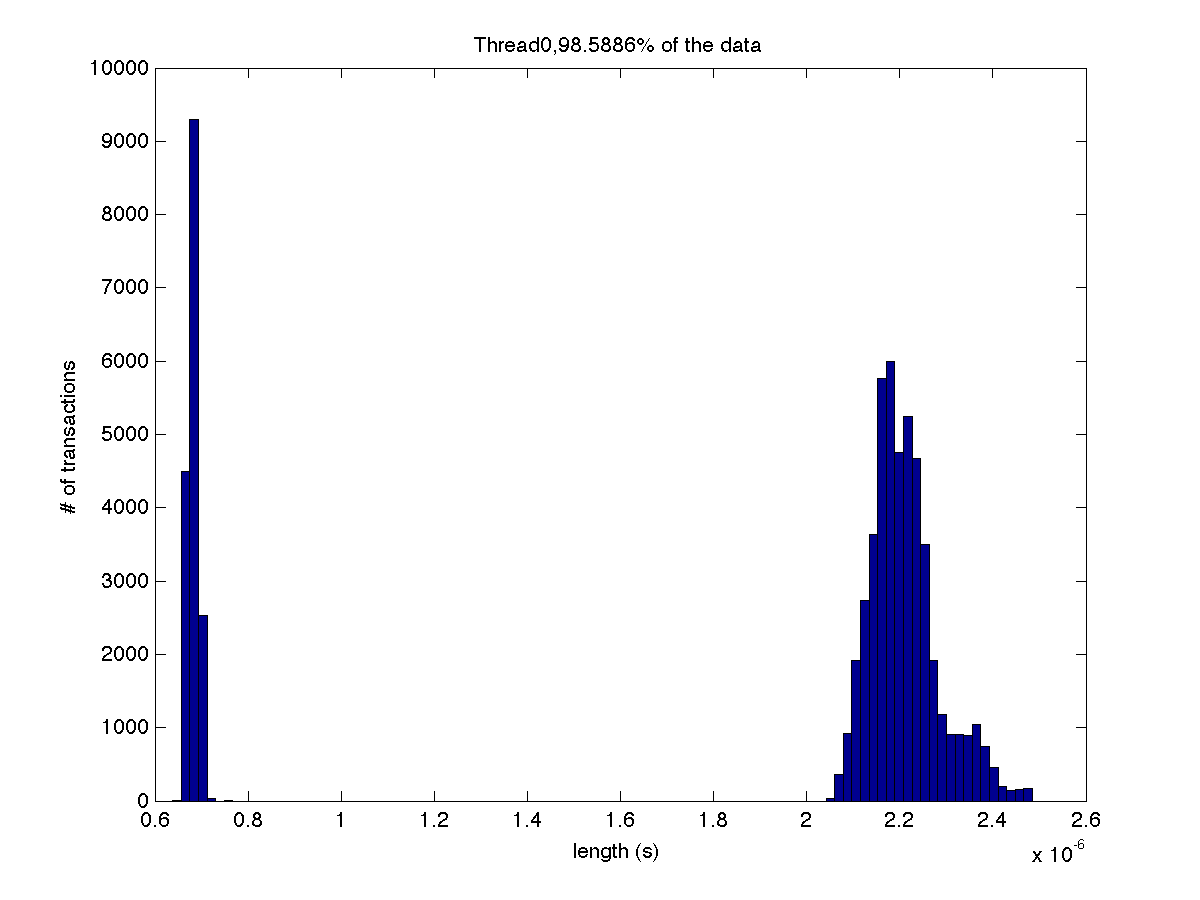
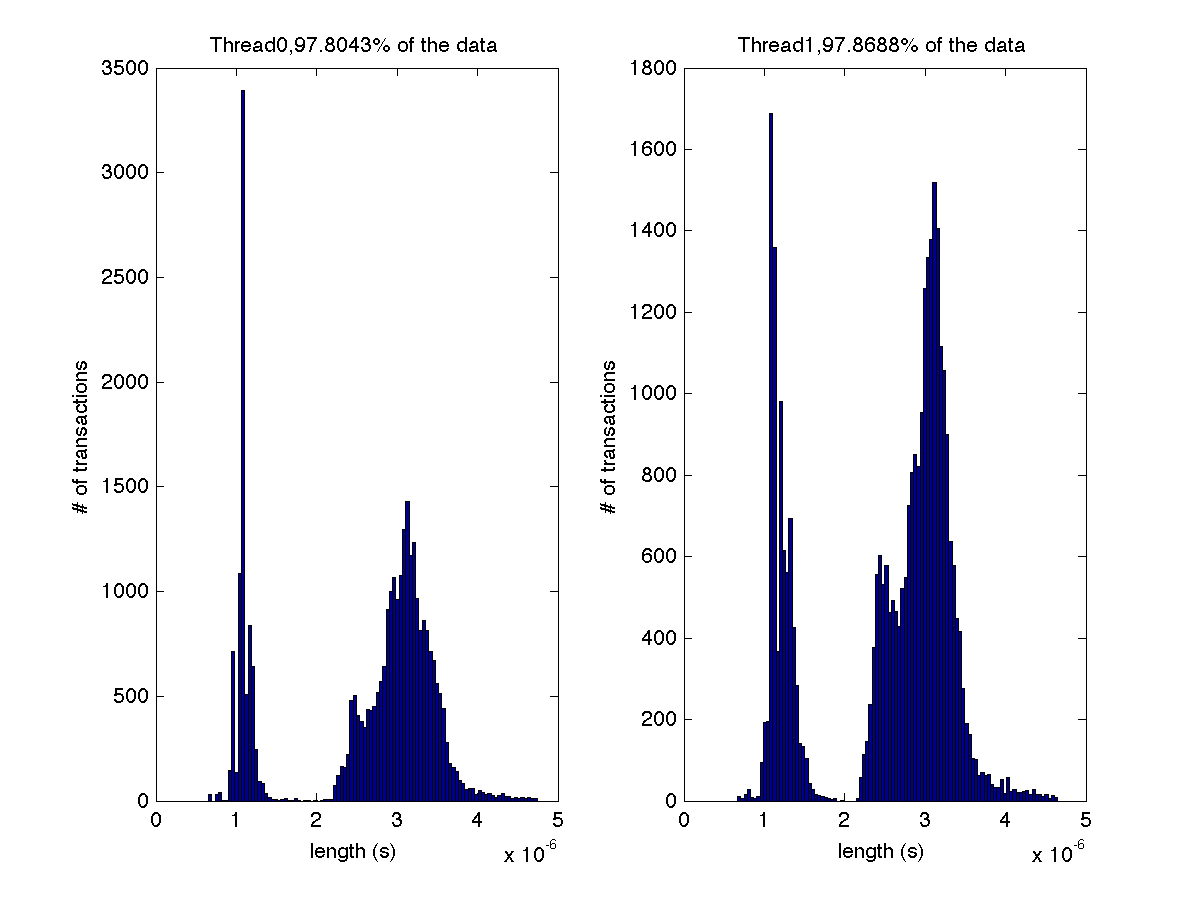
High contention - Histogram showing majority lengths of transactions for 1 thread (exact percentage in title of graph) |
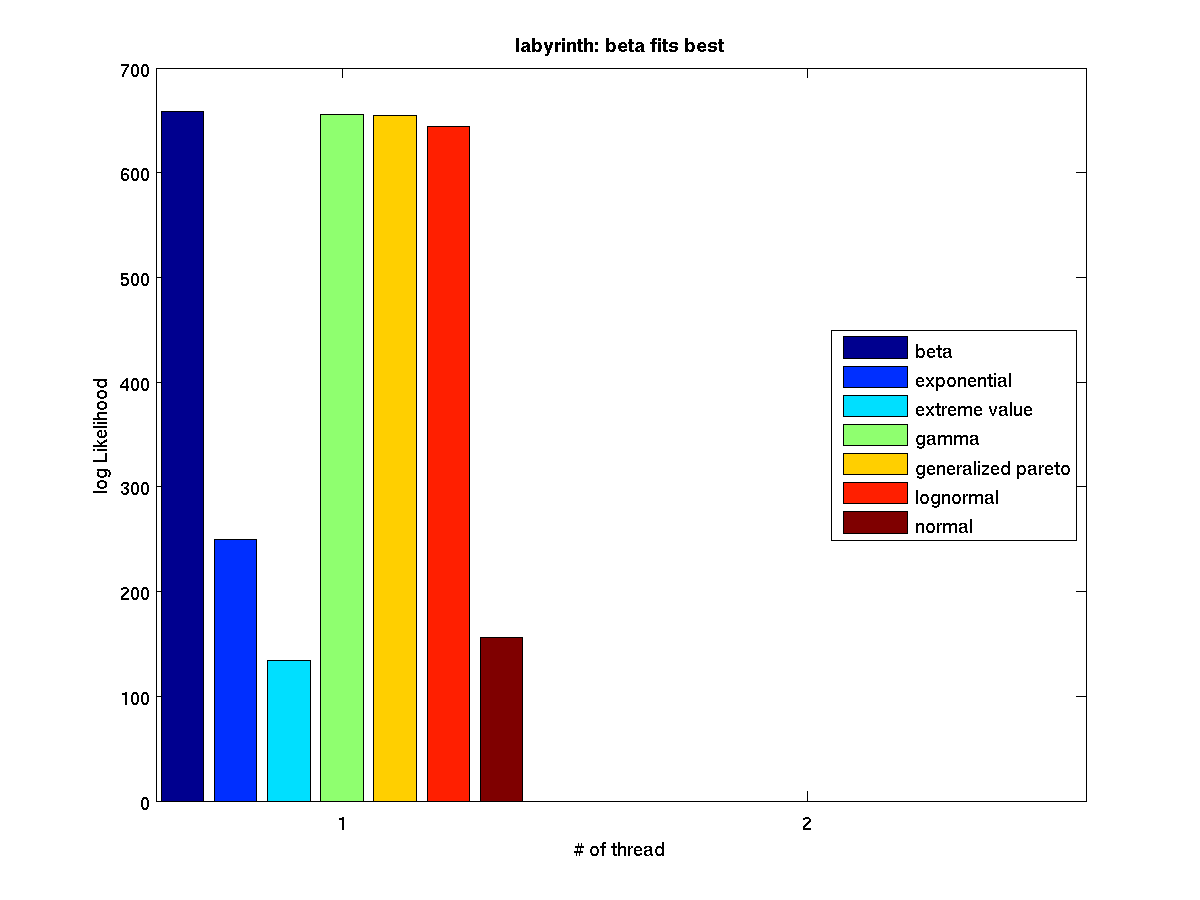
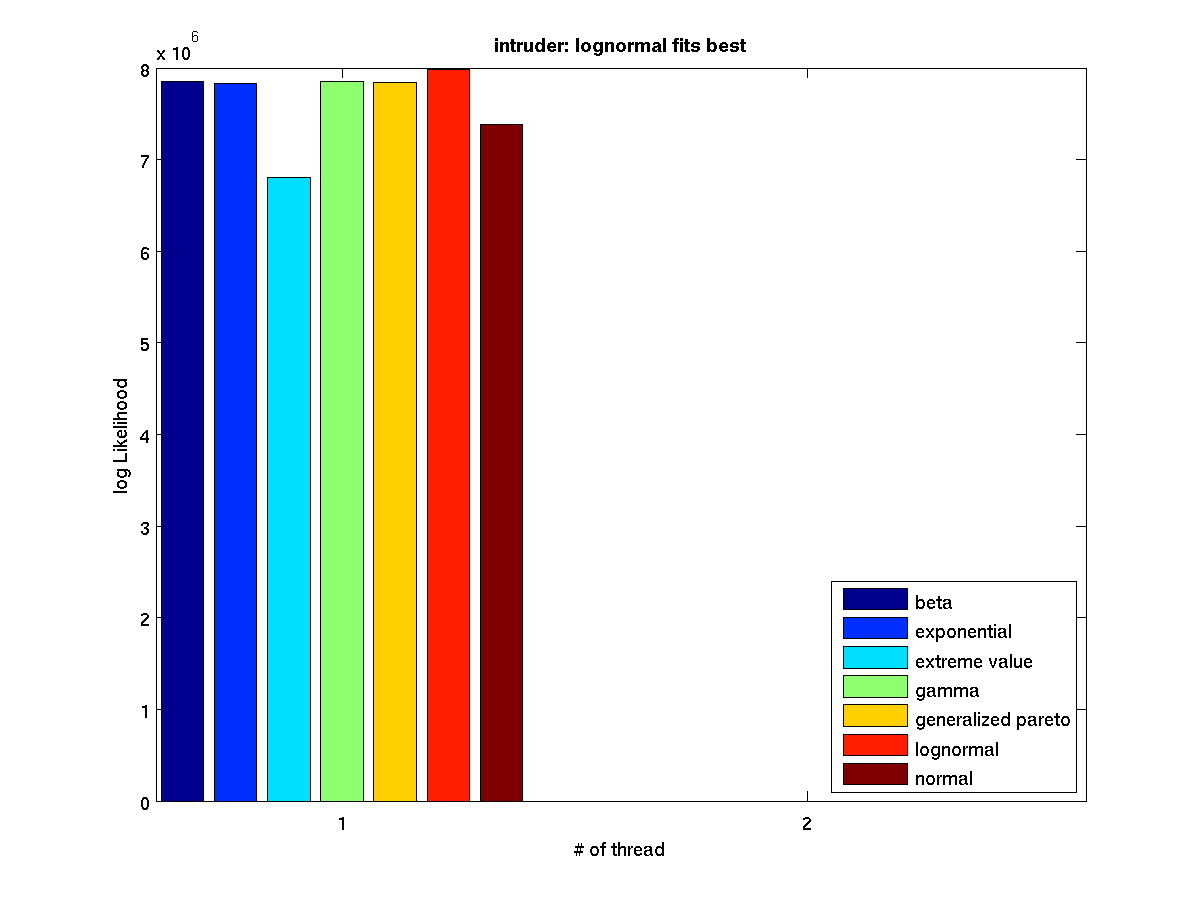
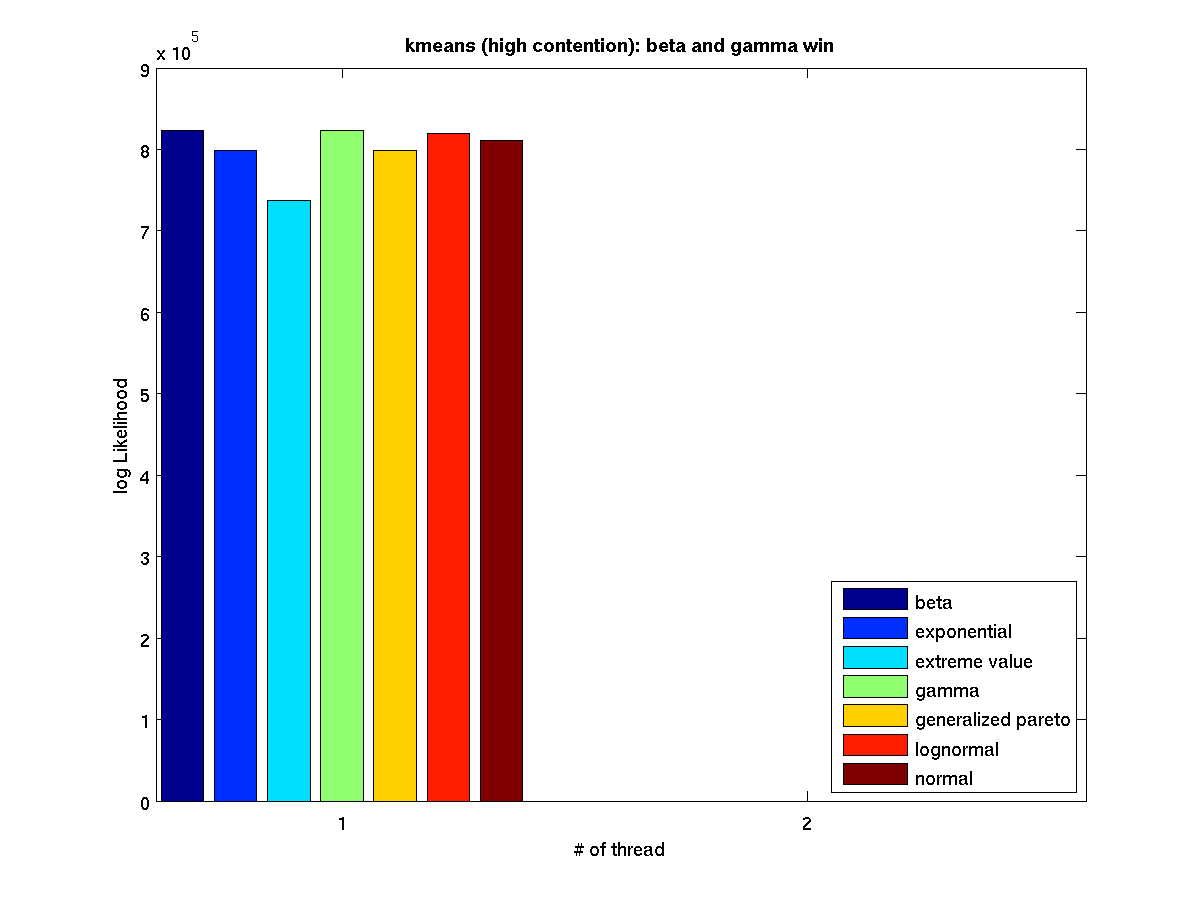
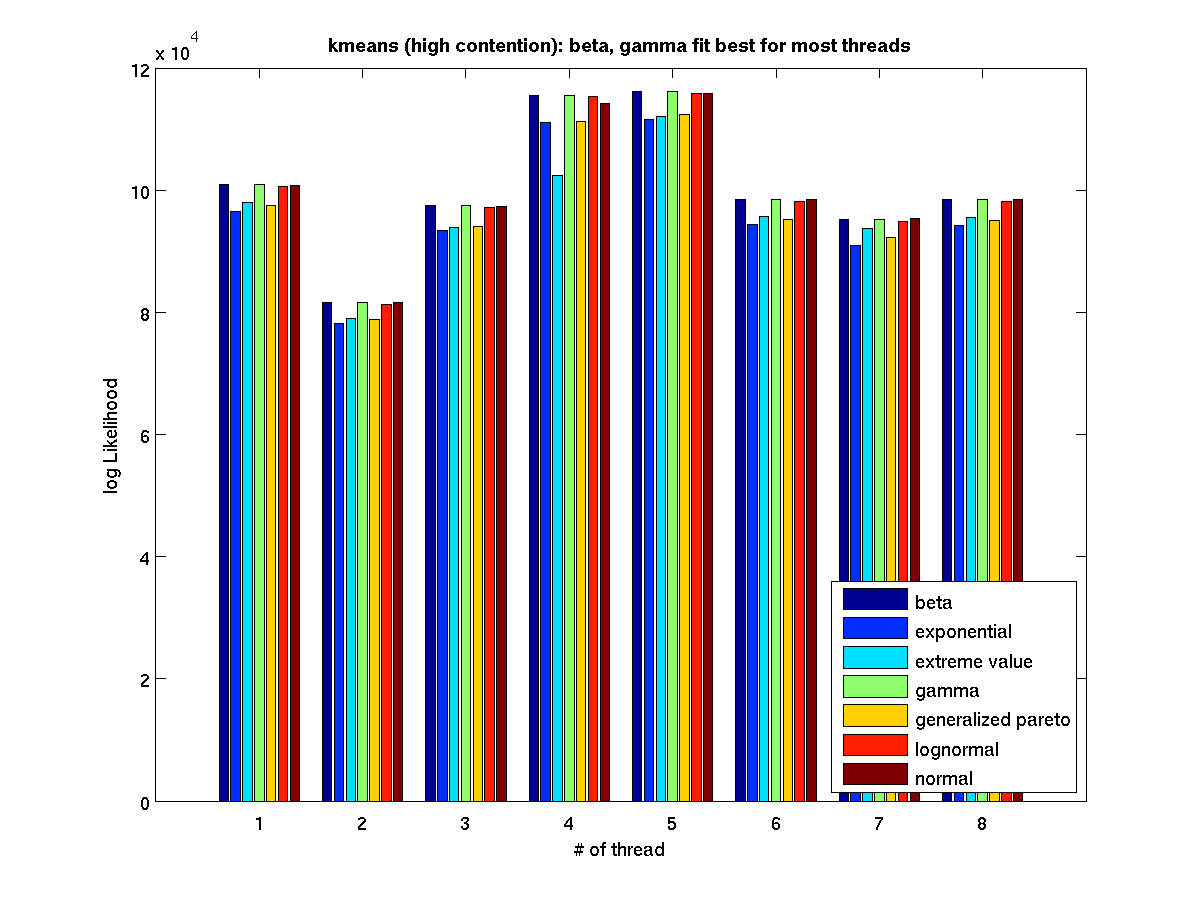
High contention - Bar graph of log-likelihood values for 1 thread |
| |
 |
 |
 |
| High contention - Boxplot of entire distribution for 2 threads |
High contention - Histogram showing majority lengths of transactions for 2 threads (exact percentages in title of graph) |
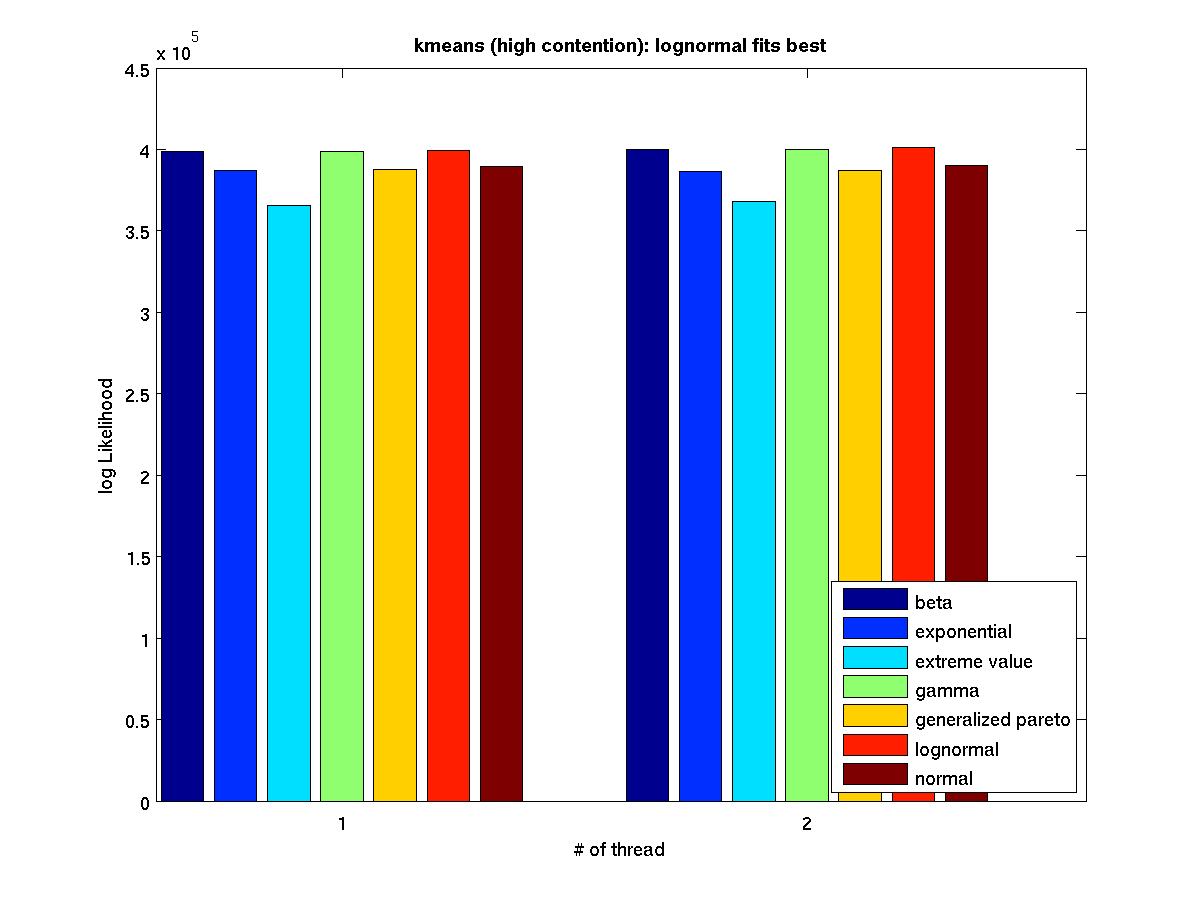
High contention - Bar graph of log-likelihood valules for 2 threads |
| |
 |
 |
 |
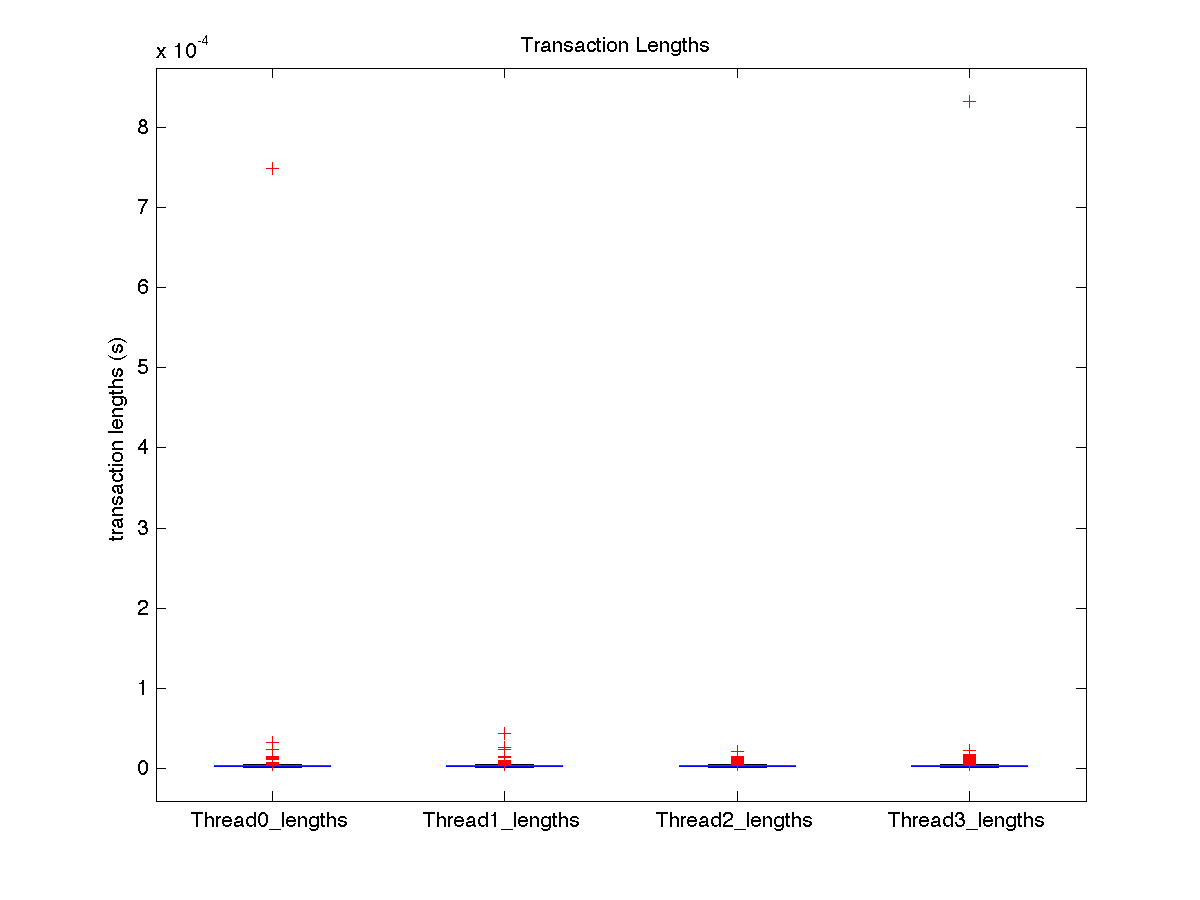
| High contention - Boxplot of entire distribution for 4 threads |
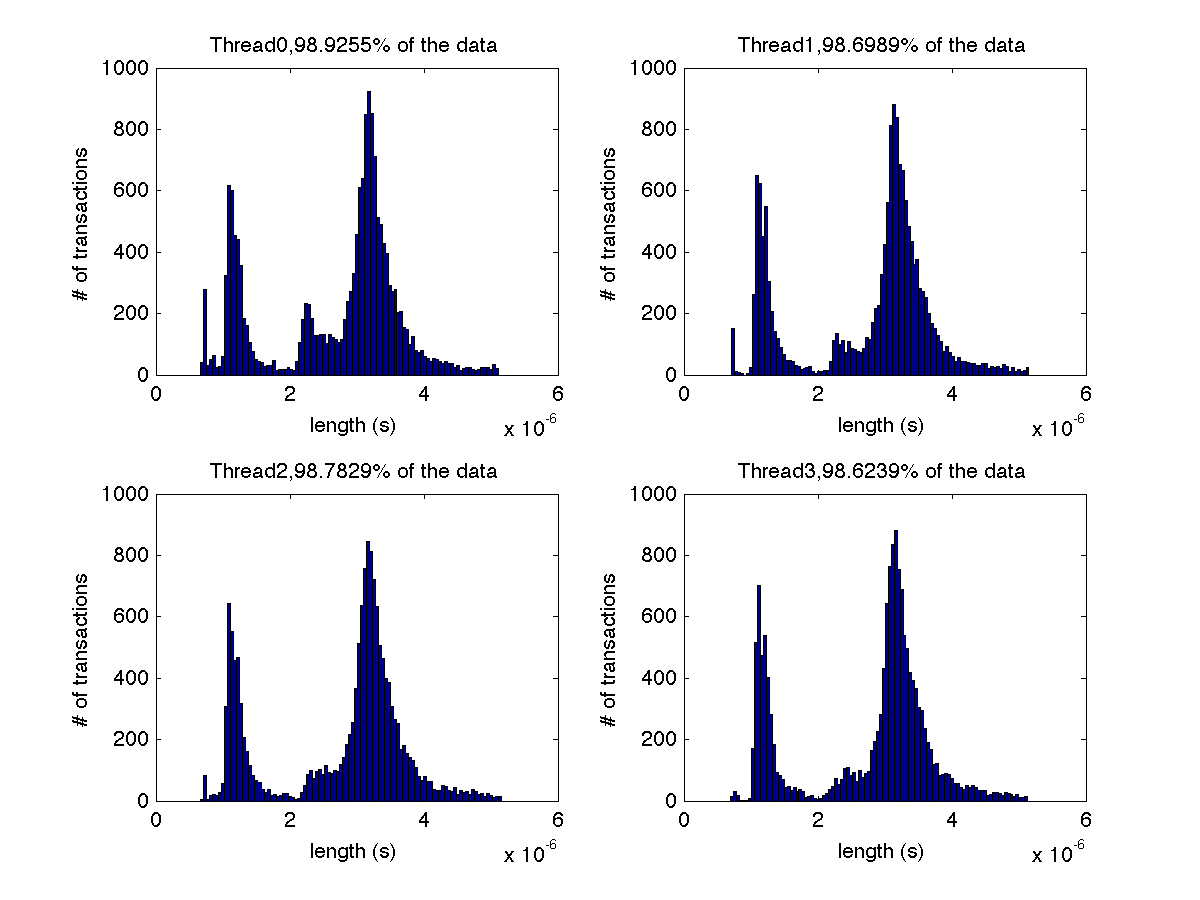
High contention - Histogram showing majority lengths of transactions for 4 threads (exact percentages in title of graph) |
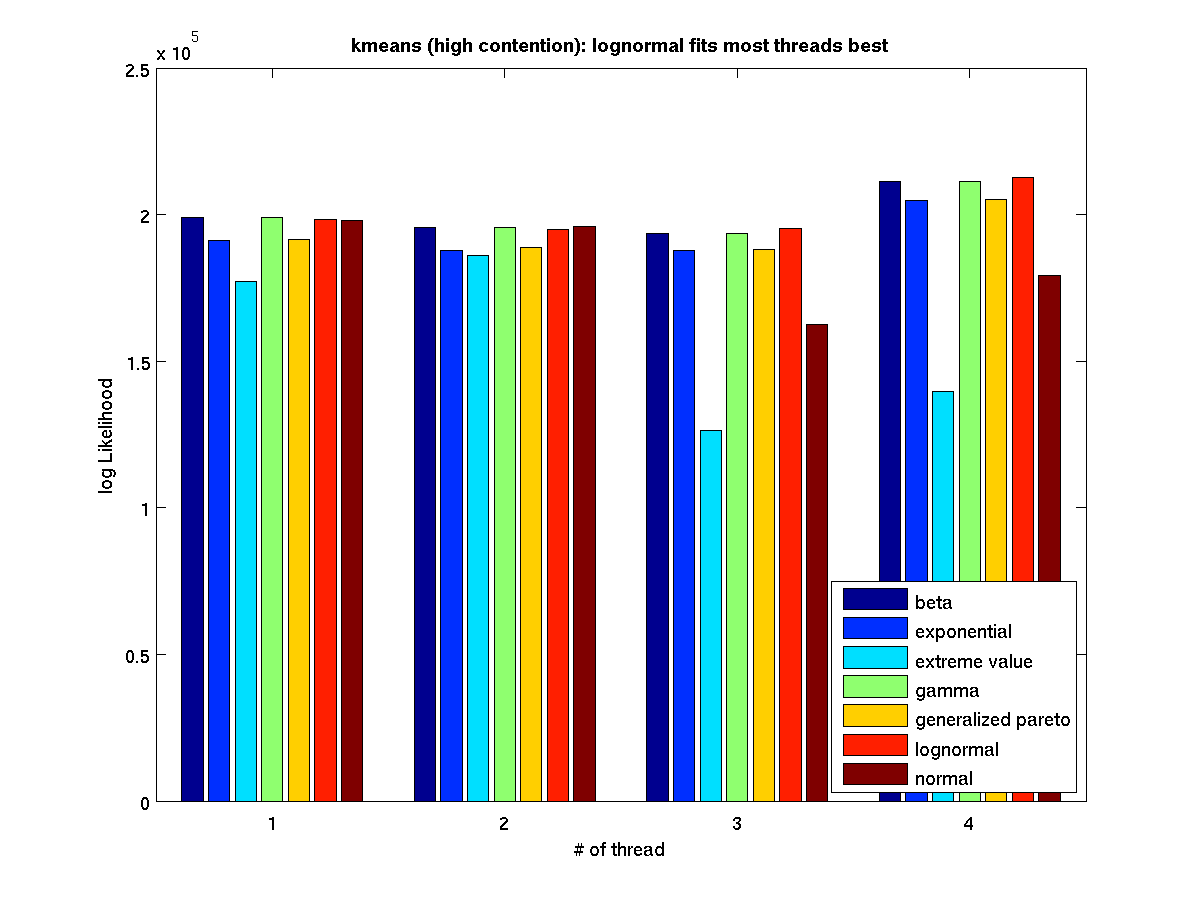
High contention - Bar graph of log-likelihood valules for 4 threads |
| |
 |
 |
 |
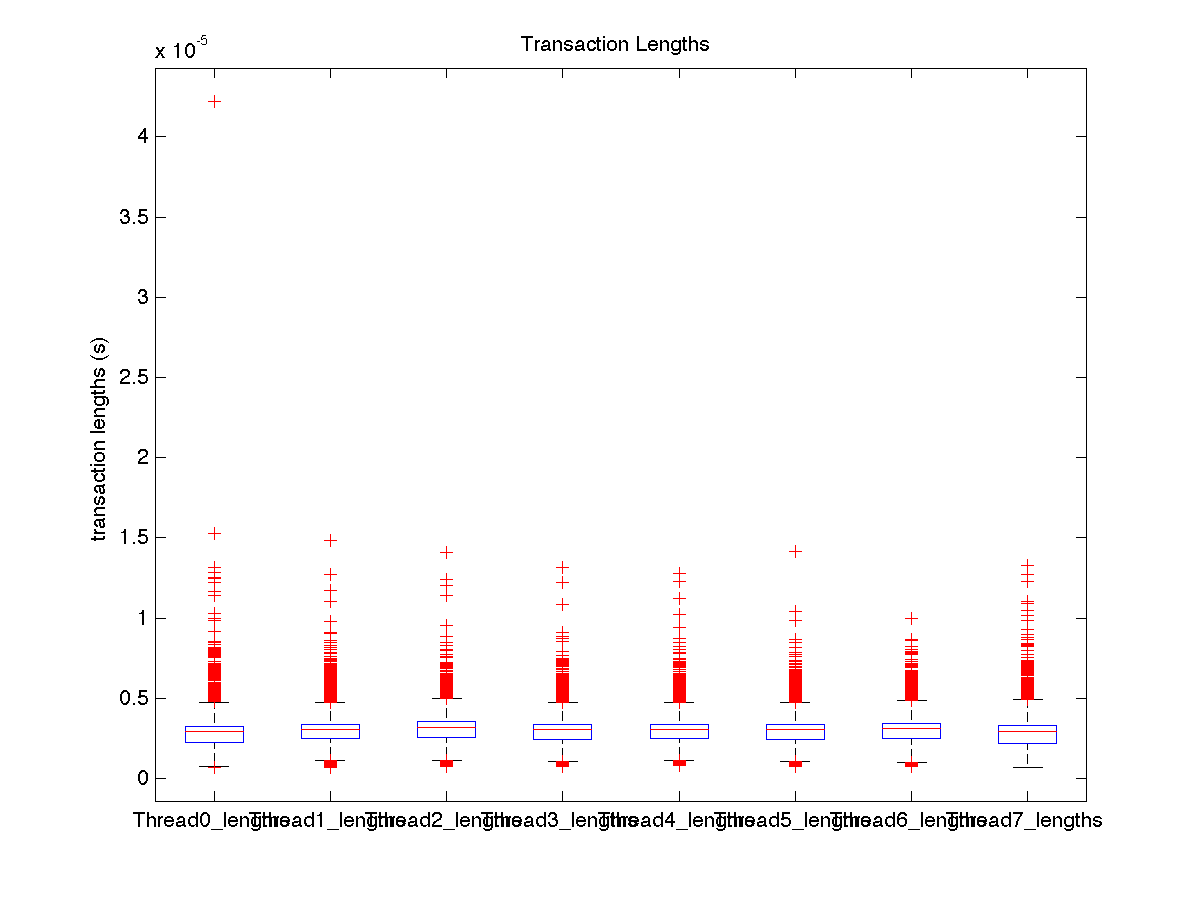
| High contention - Boxplot of entire distribution for 8 threads |
High contention - Histogram showing majority lengths of transactions for 8 threads (exact percentages in title of graph) |
High contention - Bar graph of log-likelihood valules for 8 threads |
| |