 |
So far, we have considered disjoint types of functions, i.e. functions containing stores or loads to non-local variables but no function calls, and functions containing function calls but no stores or loads. Now let us see how to analyze functions containing stores and/or loads along with function calls. Considering the three possible results from both kinds of analysis and the results from both kinds of statements, we get the 3x3 matrix drawn in table 1 for the aggregate effect on the current function. To combine the two analyses, we can do one after the other. In terms of results, there will be no difference whether we start by analyzing side effects based on stores or loads, or whether we start by analyzing side effects based on function calls. However, the decision might affect how fast we reach the results for the whole program. This will be clarified when we discuss convergence of the method in the presence of cycles next.
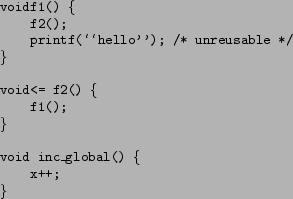
Consider the example in figure 3. Assume that f1 is analyzed first. If the method considers stores and loads first, then right away f1 will be analyzed as unreusable due to printf. When the method visits f2, because f1 has been annotated as unreusable, then f2 is also determined to be unreusable. This is the final result of the analysis, however, if the method considers function calls first, then analyzing f1 will lead it to analyze f2. When the method reaches f2 this way, it determines that a cycle exists, and the method will conditionally annotate both f1 and f2 as const. On the next step, when it considers the stores and loads in f1, it will change the annotation of f1 to unreusable. Since the method already visits f2, it might seem that the analysis is done. However, that is not the case. We need to revisit f2 because the attribute of the function it calls (f1) changes. As shown above, the method might require fewer steps by considering stores and loads first.
The above example shows how the method deals with cycles. In general, the method starts by assuming that all functions are const. It will then analyze each function for pure side effects or unreusability. Any change in the annotation of a function needs to be propagated along the call graph, including cycles. This will include changes resulting from the propagation process itself (e.g. in the above example, f2's annnotation changes as a result of the propagation of the information that f1's annotation changes). The process runs until there are no more changes of a function's annotation that needs to be propagated.
Although we have not done any formal analysis, we see some similarity between this problem--regardless of whether the method considers stores and loads first, or whether it considers function calls first--and a generic data-flow analysis problem[9]. The propagation of information along the call graph is similar to the propagation a data-flow information along a control-flow graph. In addition, the relationship const-pure-unreusable forms a finite descending chain from least to most conservative. By initially assuming functions to be const and propagating less restrictive attributes (pure and unreusable), the method will converge to the final result.