Fruits on Concrete

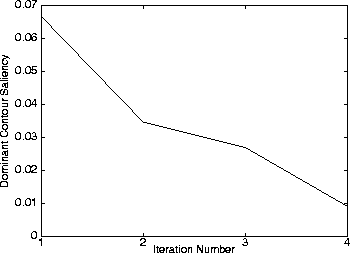
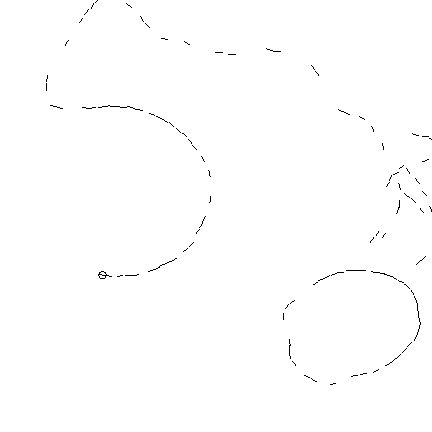
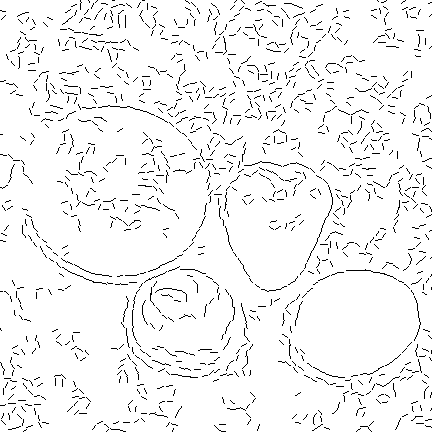Greyscale image. This is a simple scene with no occlusion. The texture of the fruit on the top left (a cantelope) is similar to that of the background. Hence an edge-detector would have difficulty finding reliable edges on some parts of the boundary of the cantelope.

Canny edge output. Note the large gaps in the bounding contour of the cantelope. Try ranking the fruits according to their saliency (i.e., in the order that they seem to pop out) before proceeding and compare with the order obtained by our segmentation algorithm. Let me know if the orders match or atleast if the first and last fruits are the same.

Saliency plot for the first iteration of the segmentation algorithm. The length of an edge is proportional to its saliency. As can be seen only one of the fruits is highlighted. The rest of the edges (even that of other fruits) are completely suppressed.

The segmentation in the first iteration. No surprises here.

Saliency plot for the second iteration of the segmentation algorithm. Before we start the second iteration, we suppress the first contour extracted to reveal the next most salient one. The first contour is suppressed by setting the affinities between all edges in the contour to zero. Note that the edges in the contour themselves are free to participate in future iterations. In the saliency plot, we observe that one of the fruits is very salient and some part of another fruit is also somewhat salient.

The segmentation in the second iteration. The fruit, part of whose contour was somewhat salient is completely ignored.

Saliency plot for the third iteration of the segmentation algorithm. Note the large gaps in that the algorithm is able to bridge with a few intermediate edges.

The segmentation in the third iteration.

Saliency plot for the fourth iteration of the segmentation algorithm.

The segmentation in the fourth iteration.

Contour saliency vs. iteration number. A closed contour is a closed sequence of edges in the contour. The saliency of the contour is the geometric mean of the affinities between successive edges in the contour. As can be seen, the segmentation algorithm indeed extracts out contours in the order of their saliencies.

First we replace the link saliencies which provide an encoding of global information (the likelihood that smooth closed contours pass through a given link) with the affinities which provide only local information. The edge saliencies are still being used to start off the segmentation algorithm. The segmentation shown is the one reported in the second iteration. The first iteration gives the same segmentation as when we use the link saliencies. Since the edge saliencies still indicate the most salient edge and since there are no large gaps in the contour bounding the first fruit, the affinities are sufficient to trace out the contour. However, in the second iteration due to gaps in the contour being traced, the segmentation breaks down.

Next, in addition to replacing the link saliencies, we also replace the edge saliencies by a local measure. The local measure that we use is the sum of the probabilities of all length-two contours that pass through the given edge. In a previous study we have found this local measure to be the most effective compared to four other measures that were proposed previously in the literature. With this local measure for edge saliencies, the segmentation breaks down in the first iteration itself.