 |
 |
 |
 |
 |
 |
 |
 |
The Quine McCluskey algorithm minimizes boolean logic. Specifically, given a boolean logic function, it will produce another boolean logic function giving equivalent output for the same inputs.
The motivation for parallelizing this project is that in computer hardware design, boolean logic minimization is used frequently, and for problems involving many terms and many implicants. Our goal was to create a fast implementation of the Quine McCluskey algorithm on multiple processors, using as many parallel "tricks" as possible, with an emphasis on learning the advantages and disadvantages of these various design techniques.
The Quine McCluskey algorithm consists of constructing a series of tables of implicants. For each table created, a new table is created (up to n tables) based on the makeup of the previous table: Any pair of implicants which differ in exactly one term is aggregated into a single implicant (with a don't-care value in place of the discrepancy) and added to the successive table. Implicants not used in the construction of any later table are then aggregated into a final list which gives the output.
Each table is dependent on the previous table, so it is not possible to directly parallelize across tables. We used a limited version of parallelizing across tables in the statically scheduled design, detailed in the static design section.
For the most part, we employed a bottom-up approach to design: First we theorized what would be needed in terms of data structures given a specific implementation strategy, and then we implemented the data structures. In general, we never used a data structure's functionality until it had been thoroughly tested. After building the building blocks, the functionality tying them all together was implemented and tested.
In order to avoid duplication of effort and redundant code, we first spent some time thinking about the overall architecture of the system and factoring out the parts that were common. In particular, we found that implicants, tables, and queues were common across all of our implementations, so we could design them independently and use them repeatedly with minimal modification.
In actuality, the common code remained mostly the same; the only significant changes were in developing a multiprocessor version of code that previously ran only on uniprocessor machines, since code for locking data structures had not yet been implemented. Additionally, multiple versions of some functions were developed: Sometimes it was necessary to assume that the data structure was locked prior to entry of the function; other times, it was necessary to assume that it wasn't. We found that the most efficient way to accomplish both goals was to write multiple functions, rather than to pass additional parameters or add indicator data members to data structures.
Despite continued analysis of results, our implementation proceeded basically as planned: The code as written near the end of the project was, at a high level, basically the same as the code as it was envisioned in the early planning stages. There were, however, changes at lower levels: Queues were introduced in various areas as attempts at optimization, and individual modules were implemented using lessons learned from the results of previous implementations.
The static design was about as boring of an implementation as anyone could possibly imagine. Pseudocode is as follows:
for each column c in table:
..for each implicant i in column c:
....for each implicant j in column c before i:
......if i and j differ in exactly one term:
........add new implicant matching i and j to column c+1
........mark j as used in a later column
..for each implicant i in column c:
....if i not used in a later column:
......add i to global list of prime implicants
There wasn't much thought involved in coming up with this approach, as there really isn't any other good way to implement the algorithm under a uniprocessor model.
The statically-scheduled design was developed chronologically after the uniprocessor design was completed. A verbatim copy of all the code was made and modifications were made to the data structures so that they could be used in a parallel environment. Additionally, some data structures were added, such as an implicant queue. The function performing most of the work was scrapped and replaced with one implementing approximately the following functionality:
wait for a new implicant i or completion of previous process
if not complete:
..for each implicant j before i:
....if i and j differ in exactly one term:
......send new implicant matching i and j to next process
......mark j as used in a later column
return to wait state
when complete:
..for each implicant i in column c:
....if i not used in a later column:
......add i to global list of prime implicants
..signal completion of this process
..add prime implicants to global prime implicant table
The main control code forked off a copy of the above code to correspond to every column in the table.
There wasn't much iterative improvement in coming up with this design. We basically did some brainstorming about the earliest point at which certain computations can proceed: As soon as the second implicant in a given pair to be compared is available, it is possible to perform that comparison and, if applicable, send the result to the next process. Upon making this observation, we then implemented an algorithm which used it to compute successive tables in a fairly straightforward fashion, resulting in the pseudocode shown above.
The dynamically-scheduled design was developed chronologically after the static design was completed. A verbatim copy of all the code was made. Not many modifications to the actual kernel of the algorithm were made, although an implicant queue queue [sic] structure was added.
The key motivation behind the dynamic design was that the statically-scheduled version suffers from severe performance issues. Later tables cannot begin computation until a good amount of computation has already taken place; similarly, computation proceeds for a long while after earlier tables have sent their final results.
To resolve this, we split up the columns into segments. In other words, what was a single queue under the static design became a queue of queues. Each process may work on part of a column, rather than being assigned to a whole column. As long as processors are kept well fed with column segments, load balancing is much improved relative to the statically scheduled design.
The shared datastructure contains one queue of segments that have not been reduced yet, and a separate "done" segment queue for every column used in the algorithm. Since processors no longer know by default which column(s) they are working with, every segment queue also contains column information.
Every thread's first priority is to look for new segments. When these are available, threads take them over and apply the reduction algorithm to them (comparing every implicant in the segment to every other.) Reduced matches are placed in a new segment to be moved to the next column over. Once a thread has finished reducing a segment, it moves it over to the "done" queue corresponding to the column the segment originated from.
The catch with column segments is that they must eventually be coalesced, because every implicant in a column must be compared to every other implicant. If there are no new segments available, the next thing a thread will try to do is look for pairs of segments in the done queues. If the thread finds such a pair, it will perform a modified reduction on it. Namely, it will make comparisons only between the two tables (as in a bipartite matching), rather than doing comparisons within the tables as well. Reducing within the tables would constitute duplicate work. Once this is done, any reductions found from the comparisons will be put in the new segment queue, with the column specification one greater than that of the two source queues. A union of the two source queues will go back into the done queue whence they came.
Once a done queue contains only a completely coalesced segment, it is truly done and any prime implicants can be collected from the segment. This condition is signalled when there is one segment present and the column records no others "checked out," or pending completion by some thread. More than one such done queue can be in the process of having prime implicants copied out at a time, although the global prime implicant table is protected by a lock.
The initial segment size -- used when the set of input implicants is partitioned -- can be set on the command line. Segment sizes will vary as the program runs.
Results were taken from batch jobs processed on 64-processor SGI Origin 2000 machines at NCSA. Data sets, too large to be included here, are available at http://www.cs.cmu.edu/~mid/495/datasets.
 |
 |
 |
 |
 |
 |
 |
 |
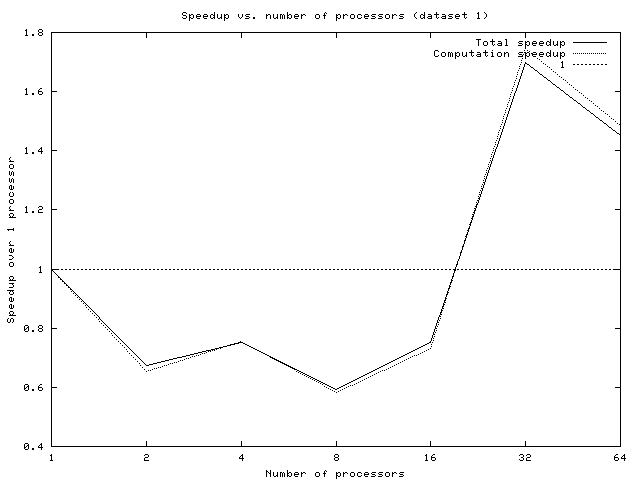
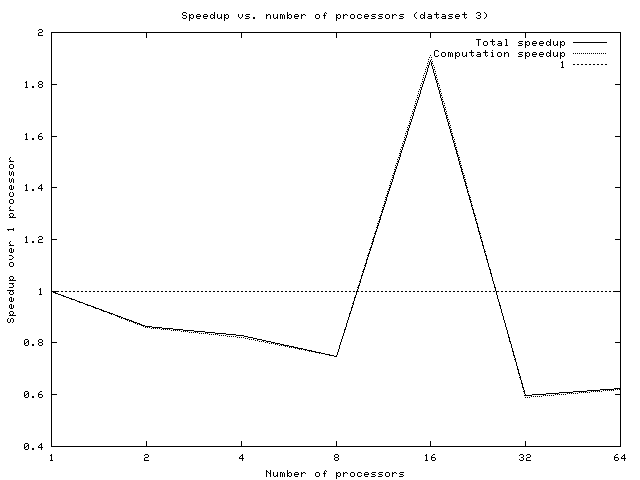
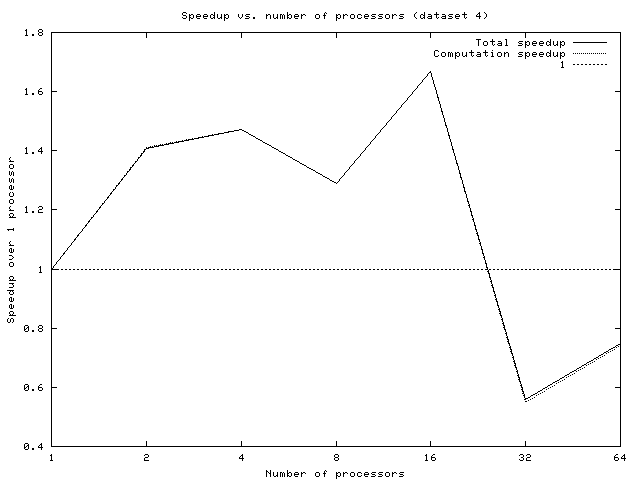
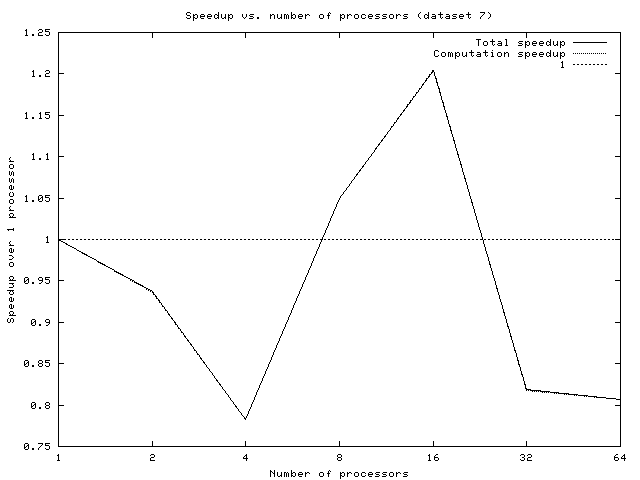
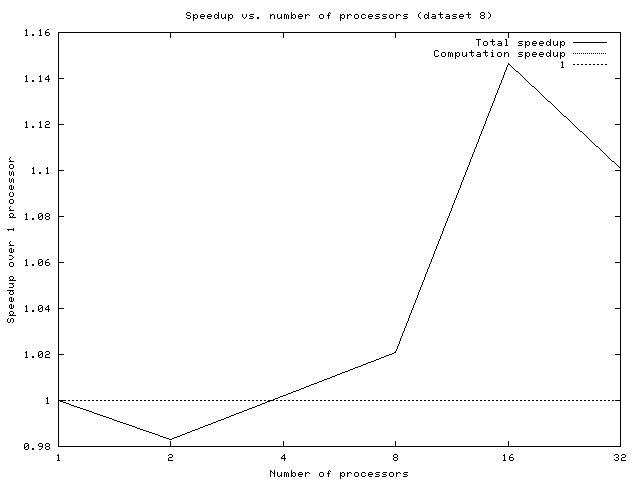
The only real common trend is that the speedup usually seems to peak at around 16 processors. However, since the speedups never passed 2.0, we conclude that the particular statically scheduled implementation we chose is unlikely to be embraced by the industry as an earth-shaking improvement. Furthermore, due to inherent limitations of this approach (discussed in the dynamic design section), we feel that any statically scheduled implementation of Quine McCluskey will produce similarly dismal performance.
The dynamic results were somewhat more hopeful than the static results,
though still not as ideal as we would like them to have been. Below is a
graph of time taken for varying number of processes; runs with more
processors also ran on proportionally large datasets, so as to compensate
for overhead:
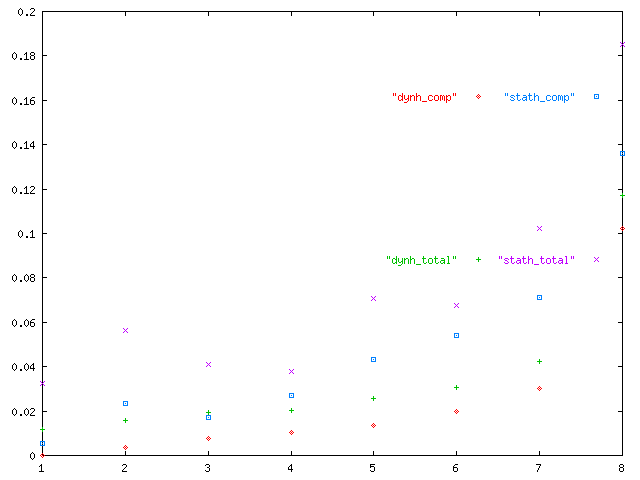
Here is a graph showing the total time (in seconds) plotted
logarithmically versus the number of processors:
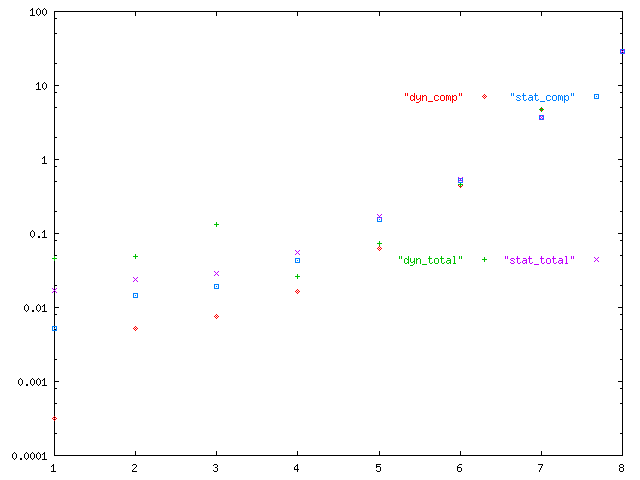
We can see from these graphs that the overhead is significant when the amount of work is small; there is also an appreciable amount of overhead involved with increasing numbers of processors. It is fairly obvious, however, that the dynamic implementation seems to run more quickly than the static version.
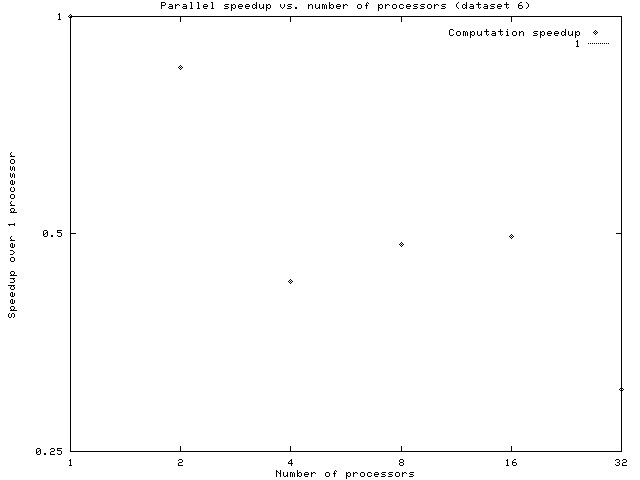
Overall speedups are shown below:
 |
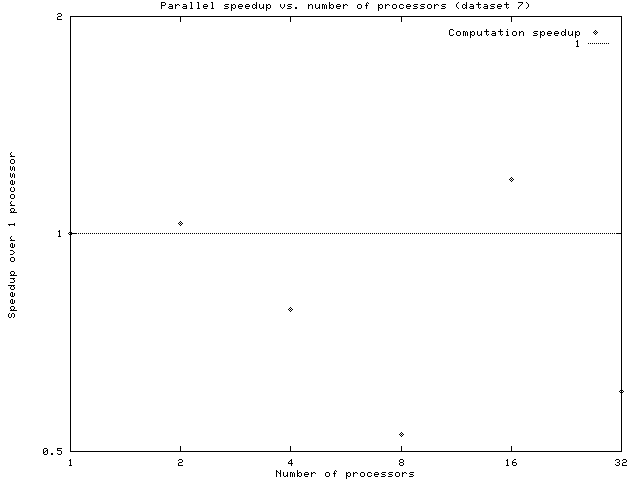 |
Although dynamic timing results were almost always significantly better than the static ones, that isn't saying a lot. Especially for small file sizes, the code does not scale well, and speedups are actually slowdowns. Around 2^7 implicants, the situation improves, providing small speedups for larger numbers of processors. The suspicion is that load-balancing is still bad. Even if work is evenly distributed from the beginning, there is the potential for it to become unbalanced over time. These are likely problems:
We came up with a number of things which, given more time, we would work on in an attempt to improve performance:
The work was distributed approximately as follows:
A single individual identified with a project indicates that that individual was the coordinator of that segment of the project and/or did the formative work in that area. We emphasize that in general, both people gave substantial input to each portion. Furthermore, the tasks listed above were not equal in time or difficulty. Given an overall analysis of the work on the project, we feel that credit for the work done here should be distributed evenly.
It appears that static scheduling of any type is doomed to failure in Quine McCluskey, since it is a very irregular problem, and it is impossible to know ahead of time where the majority of work will be concentrated. Our static results were very erratic. We suspect that this may be due to irregularities in the datasets we used to time the problem. The erratic nature of our static results was one of the most surprising things we found, although its bad performance was not unexpected.
The dynamically scheduled version was more effective with parallelizing the problem. We suspect that the better performance is mainly due to our approach of working on the problem in a divide-and-conquer fashion, something which is widely applicable to many diverse challenges in software engineering, but especially to parallel programming. However, we still were not quite able to reach an effective speedup.
The vast difference between our two implementations underscores the fact that a program is not faster just because it uses multiple processors; an effective implementation requires good programming skill and familiarity with parallel programming techniques, as well as an ability to analyze performance shortcomings and formulate improvements.
We learned in this project how to deal with some of the issues arising in parallel development, such as: achieving good load balancing; avoiding unnecessary locking and lock contention; avoiding global memory access in favor of local copies, especially when a lot of writes are taking place; summarizing results locally and then updating a global summary, rather than summarizing results by making repeated accesses directly on the global summary.
In addition to gaining familiarity with different parallel programming paradigms, we learned ways of blurring the lines between them in order to achieve objectives. For example, the version that we called dynamically scheduled had aspects of both static and dynamic scheduling, and both of our parallel implementations blurred the lines between the shared address space paradigm and the message passing paradigm.