For this assignment, I implemeted A* as modularly as possible while retaining the assumption of operating in SE(2) so that the speedup from hardcoding optimizations dependent thereon could be maintained. Specifically, the heuristic, motion model, and robot model (e.g., its shape for obstacle-detection purposes) can be easily swapped. The implementations of the predecessor data structure and the "visited" node list were likewise pluggable, but the simple implementations I came up with (statically allocating the space for the entire map for each) proved sufficient given the relatively smalls maps I worked with.

As the heuristic, I used the function abs(delta theta, in action steps) + [euclidean distance]. This was reasonable because the corresponding motion models I used engendered a cost of 1 for each forward/backward step or rotation-step (typically Pi/4). Thus, it was always an underestimate (and hence admissable) without being wildly inaccurate.

The motion model I used assumed a differential-drive robot (independent of the shape) that could rotate in place one rotation-step at a time or take varying length motions (with correspondingly varying costs) forward or backward along the same orientation.

For the robot shape model, I treated the robot as an arbitrary polygon and performed polygon intersection testing between it and a likewise-polygonal obstacle world to determine whether a given position was blocked. This allows me to, for instance, make the robot an "L" shape and then build a world consiting of keyholes through which it must wiggle. I am not demonstrating this here, but I may toy with this later on. I could also just as easily have made the robot circular by implementing the appropriate class, but polygonal seemed to offer greater opportunities.

The overall algorithm can be summarized as follows:

• Q.push(start)
• while(currstate = q.pop())
  • if (currstate == goal) return SUCCESS;
  • visitedmap.mark(currstate);
  • getSuccessors(currstate, succs);
  • foreach succ (succs[i].pos)
    • if (visitedstates.isMarked(succ) || obsmodel.isBlocked(succ)) continue;
    • h = getHeurDist(succ, goal);
    • newcost = currstate.cost+succs[i].action.cost;
    • prevsucc = q.find(succ);
    • if (prevsucc != NULL)
      • if (newcost < prevsucc.cost)
        • prevsucc.cost = newcost;
        • predmap.setPred(succ,{currstate,succs[i].action});
    • else
      • q.push(succ, newcost+h);
      • predmap.setPred(succ,{currstate,succs[i].action});
• (If reached), return FAILURE

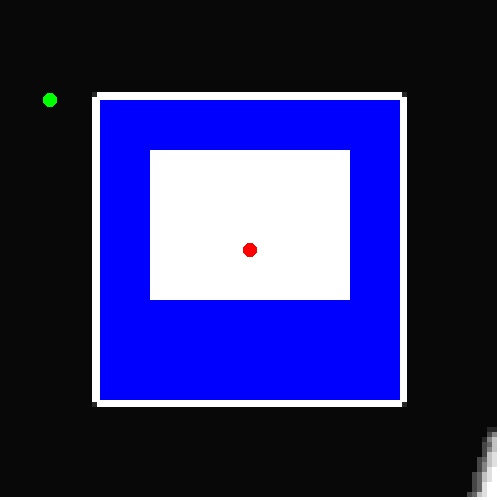
In the following images and the videos, the opacity of the planning "flood" represents the number of orientations reached (popped off the priority queue) at each 2-D position. Essentially, it's a 2-D visualization of 3-D data.

In these runs, a square 3x3 robot shape is used.

Successful run
Partway through:

Completed:

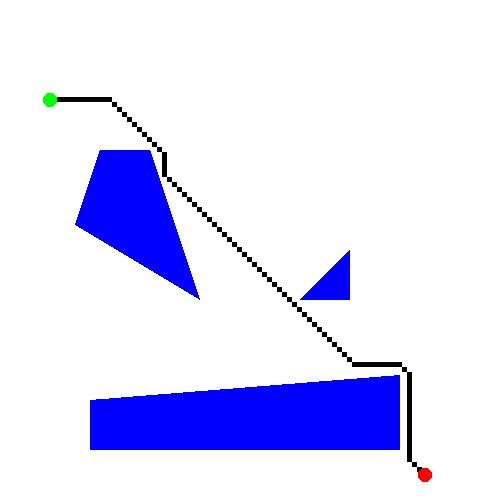
Unsuccessful run
Halfway through:

Completed:

Source code: Available here
Videos: Available here

This appears to compile and run fine on linux.andrew.cmu.edu, and should do the same on most other Linux systems. No attempt was made to target other OSes.