Homework 7

16-735

Ross Knepper

21 November 2007

The purpose of this assignment is to implement a probabilistic roadmap algorithm for a planar robot arm of four or more links. I have selected to implement RRT on this arm. In fact, the implementation is essentially independent of the number of links in the arm. The outline of the algorithm follows.

First, start and goal configurations for the arm must be specified. In this case, the C-space is joint-angle space,for a d-dimensional robot. The start state is inserted into the set of visited nodes, which will be referred to as the closed list. Then, the iteration begins. Each iterative step starts by randomly selecting a target configuration. With probability 0.1, the goal configuration is chosen as the target. Otherwise, the target is randomly chosen. Each joint angle is uniformly sampled from the set [-π ... π). The closed list state then returns the nearest neighbor to the target state. For efficiency, this would typically be implemented with a kd-tree, but for this application, a simple C++ STL vector gave adequate performance. Nearest neighbor is measured in joint angle space, meaning that angles wrap around. The distance in the shorter direction is chosen for each joint angle, and then the Euclidean distance is computed.

Once the node nearest to the target is selected, the expansion step begins. We want to extend the graph from the nearest state in the direction of the target. However, the distance is capped at 2 because it appeared to give good results. The candidate state is placed at either 2 units from the nearest state or at the target if it is closer than 2 units. We must then test that there is a free path connecting the nearest state and the candidate state. Rather than testing for intersection with a complex swept volume, the path between the nearest and candidate states is finely sampled (every 1.5% of the path length), and each configuration is tested for collision with the environment. The path connecting states is is defined as that in which each joint moves at a constant rate, arriving at the destination configuration in equal time. If the path is found to be collision free, then the candidate state is added to the closed list (and thus to the graph). Otherwise, the candidate state is discarded and the algorithm continues.

The algorithm terminates when the goal configuration is reached. It will run forever if no path exists. It will take a much longer time if a narrow corridor in the configuration space must be traversed. The examples below show a somewhat-narrow corridor.

The first example is a four-link manipulator in a workspace with three obstacles. The empty world appears like this:

A time-lapse picture of all the successful (collision-free) candidate states searched by the algorithm is shown here (note purple solution path of end effector):

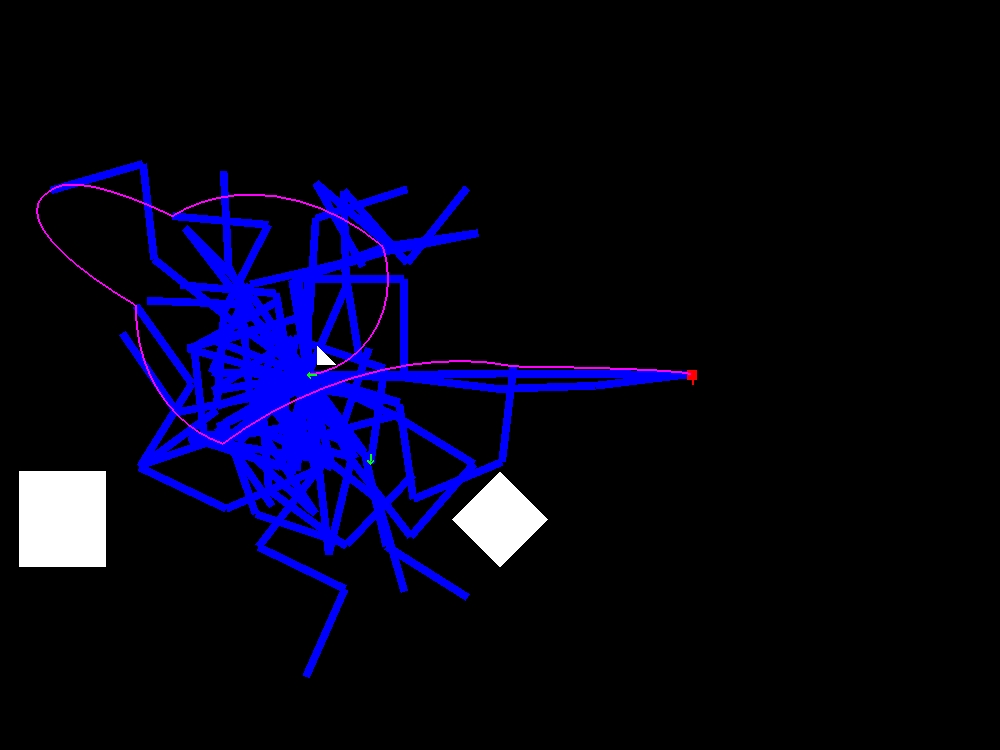
Finally, a video shows every edge being searched (gray lines) and then the final path plan being executed (purple lines at end).

To show the extensibility of the algorithm, an 8-link arm was also tested. The only change was that an extra four parameters were added to the start and goal configurations. The algorithm works identically on any number of links.