
programming-by-demonstration, PBD, automated text editing, pattern matching, search-and-replace, LAPIS
Multiple selection - the ability to select multiple, discontiguous objects and apply the same operation or property change to all the selected objects - is common in drawing editors and file managers. But it is virtually unheard-of in text editing, which is unfortunate. In this paper, we show that multiple selection can deliver a wide array of benefits, including better user feedback, fast and accurate inference, novel forms of intelligent assistance, and the ability to selectively override system inferences with manual corrections.

To experiment with multiple selections in text editing, we have developed a new text editor called LAPIS (Figure 1). Although LAPIS offers several ways to make a multiple selection without inference, including mouse selection and pattern matching, our primary concern in this paper is inferring a multiple selection from examples. LAPIS has two techniques for inferring multiple selections:
Multiple selections are a good way to give feedback to the user about the system's inference. After the user gives an example and the system makes a new inference, the user can scroll through the text editor to see what is selected by the system's inference, and what isn't. LAPIS also describes the inferred selection with a pattern. Providing both kinds of feedback reinforces the user's understanding of what the system is doing.
When the file is large, scrolling through it to check the inferred selections can be tedious. LAPIS alleviates this problem somewhat by augmenting the scrollbar with marks indicating where selections can be found. Even more useful is outlier highlighting, which draws attention to unusual selections that might be inference errors.
Previous papers have described some of these techniques. Simultaneous editing was introduced in a USENIX paper [7] that discussed only its second step, inferring the user's editing selections after the record set has already been defined some other way (i.e. not by inference). This paper completes the picture by describing the first step, showing how the record set can be inferred from examples, with a novel regularity heuristic to rank hypotheses and reduce the number of examples required. Outlier highlighting was described in a UIST paper [8], and is mentioned here as a new form of intelligent assistance enabled by multiple selections. Selection guessing is completely new to this paper.
LAPIS finds its roots in programming by demonstration (PBD). In PBD, the user demonstrates one or more examples of a program, and the system generalizes the demonstration into a program that can be applied to other examples. PBD systems for text editing have included EBE [10], Tourmaline [9], TELS [11], Eager [2], Cima [5], DEED [3], and SMARTedit [12].
None of these systems used multiple selection for editing or feedback about inferences. Multiple selections completely reshape the dialogue between a PBD system and its user. While a traditional PBD system reveals its predictions one example at a time, multiple selections allow the system to expose all its predictions simultaneously. The user can look and see that the system's inference is correct, at least for the current set of examples, which in many tasks is all that matters. Novel forms of intelligent assistance, such as outlier highlighting, can help the user find inference errors. The user can correct erroneous predictions in any order, not just the order chosen by the PBD system. Alternative hypotheses can be presented not only abstractly, as a data description or pattern, but also concretely, as a multiple selection. If the desired concept is unlearnable, the user may still be able to get close enough and fix the remaining mispredictions by hand, without stopping the demonstration.
The system that most closely resembles multiple selection in LAPIS is Visual Awk [4]. Visual Awk allows a user to create awk-like file transformers interactively. Like awk, Visual Awk's basic structure consists of lines and words. When the user selects one or more words in a line, the system highlights the words at the same position in all other lines. For other kinds of selections, the user must select the appropriate tool: e.g., Cutter selects by character offset, and Matcher selects matches to a regular expression. In contrast, LAPIS is designed around a conventional text editor, operates on arbitrary records (not just lines), uses standard editing commands like copy and paste, and infers selections from examples.
This section describes multiple selection and inference in LAPIS from the user's point of view. We first explain how to use multiple selections for text editing without inference. Then we discuss two techniques for inferring multiple selections: selection guessing and simultaneous editing.
LAPIS (Lightweight Architecture for Processing Information Structure) is based on the idea of lightweight structure [6], a library of patterns and parsers that detect structure in text. The LAPIS library includes parsers for HTML, Java, document structure (words, sentences, lines, paragraphs), and various codes (URLs, email addresses, phone numbers, ZIP codes, etc). The library can be easily extended by users with new parsers and patterns. Part of the structure library can be seen in the lower-right corner of Figure 1.
The structure library is a powerful tool for both learning agents and users. For a machine-learning agent, the library is a collection of high-level, domain-specific concepts that would be difficult or impossible to learn otherwise (e.g. Java syntax). For a user trying to write a search-and-replace pattern, the library offers predefined patterns as building blocks.
The structure library is also the easiest way to make a multiple selection in LAPIS. Clicking on a name in the library selects all the occurrences of that concept in the editor. Figure 2 shows some multiple selections made this way.
 |
 |
A close look at Figure 2 reveals that LAPIS selection highlighting is subtly different from conventional text highlighting. All GUI text editors known to the authors use a solid colored background that completely fills the selected text's bounds. Using this technique for multiple selections has two problems. First, two selections that are adjacent would be indistinguishable from a single selection spanning both regions. We solve this problem by shrinking the colored background by one pixel on all sides, leaving a two-pixel white gap between adjacent selections. Second, two selections separated by a line break would be indistinguishable from a single selection that spans the line boundary. We solve this problem by adding small handles to each selection, one in the upper left corner and the other in the lower right corner, to indicate the start and end of the selection. These small changes presented no difficulties for the users in our user studies, who were able to understand and use the highlighting without any explicit instruction.
Another way to make a multiple selection is pattern-matching. LAPIS has a novel pattern language called text constraints [6], which is designed for combining library concepts with operators like before, after, in, and contains. Examples of patterns include "-" in PhoneNumber, Link containing "My Yahoo", last Word in Sentence, and Method containing MethodName="toString". (The capitalized words in these patterns are concepts from the structure library.) Running a pattern selects all matches to the pattern.
The user can also make a multiple selection with the mouse. As in other text editors, clicking and dragging in the text clears the selection and makes a single selection. To add more selections, the user holds down the Control key while clicking and dragging. To remove a selection, the user holds down Control and clicks on the selection. Selections can be added and removed from any multiple selection, so a multiple selection created by pattern matching can be manually adjusted with the mouse.
A multiple selection can include insertion points as well as regions. An insertion point is a zero-length selection between two characters. As in other text editors, an insertion point is selected by clicking without dragging. Multiple insertion points are selected by holding down Control and clicking. Insertion points can also be selected by a pattern, such as point ending Line or point just before ",".
Once a multiple selection has been created, editing with it is a straightforward extension of single-selection editing. Typing a sequence of characters replaces every selection with the typed sequence. Pressing Backspace or Delete deletes all the selections if the multiple selection includes at least one nonzero-length region, or else just the character before (or after) each insertion point if the selection is all insertion points. Other editing commands, such as changing character styles or capitalization, are applied to each selection.
Clipboard operations are slightly more complicated. Cutting or copying a multiple selection puts a list of strings on the clipboard, one for each selection, in document order. If the clipboard is subsequently pasted back to a multiple selection of the same length, then each string in the clipboard list replaces the corresponding target selection. If the target selection is longer or shorter than the copied selection, then the paste operation is generally prevented, and a dialog box pops up to explain why. Exceptions to this rule occur when the source or the target is a single selection. When the source is a single selection, it can be pasted to any number of targets by replication. When the target is a single selection, the strings on the clipboard are pasted one after another, each terminated by a line break, and an insertion point is placed after each pasted string. Line breaks were chosen as a reasonable default delimiter. The user can easily delete the line breaks or replace them with a different delimiter using the new multiple selection.
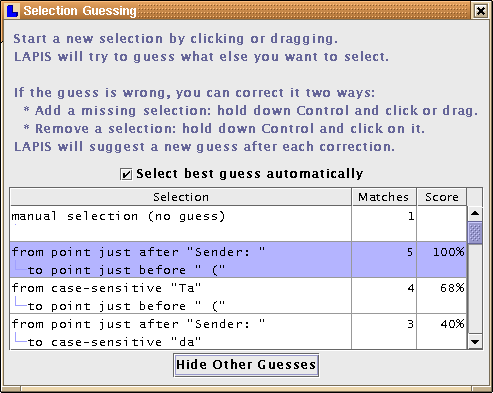
The most general inference technique in LAPIS is selection guessing. Selection guessing is a mode in which every selection added or removed by the mouse is used as a positive or negative example for inference, producing a multiple selection that is consistent with the examples. The hypothesis is displayed both as a multiple selection in the editor, and as a pattern in another pane.
As long as selection guessing mode is active, LAPIS displays a modeless dialog box showing some alternative hypotheses for the user to choose from (Figure 3). The user can click on any hypothesis to see the corresponding multiple selection in the editor. The hypotheses are ranked by a score based partly on the pattern's complexity and partly on the regularity heuristic described below.
The dialog box also includes some controls that inhibit inference. When ``Select best guess automatically'' is checked (the default), the system automatically changes the multiple selection after each example to reflect the current best hypothesis. When this option is unchecked, however, the system never changes the selection autonomously, but merely updates the dialog box with its latest hypothesis. The user must click on the hypothesis to view it.
Turning off automatic guessing allows the user to make a series of corrections without having the selection changed by a new hypothesis after each correction. These features were motivated by user study observations. In principle, if a selection is learnable, then turning off automatic guessing would be unnecessary, because the user's corrections would eventually converge to the desired selection. In practice, however, users have no way to predict whether the desired selection is learnable or how many examples it might take. As a result, as soon as an almost-correct hypothesis appeared, users expressed a desire to make the system stop guessing and let them fix the exceptions manually. Turning off automatic guessing makes this possible.
If the desired selection is outside the hypothesis space, inference will eventually fail to find a hypothesis consistent with the examples. When inference fails, the system stops guessing. The user can continue correcting the last successful hypothesis manually. LAPIS keeps a history of recent hypotheses, so the user can return to a previous hypothesis which might have been closer to the desired selection.
Once the desired multiple selection is made, the user can edit with it as described in the previous section. While the user is typing or deleting characters, no inference is done. When the user starts a new selection, the set of examples is cleared and the system generates a fresh hypothesis.
Many repetitive tasks have a common form: a group of things all need to be changed in the same way. Some examples from the PBD literature include:
These tasks can be represented as an iteration over a set of text regions, which we call records for lack of a better name, where the body of the loop performs a fixed sequence of edits on each record. LAPIS addresses this class of tasks with a special mode called simultaneous editing.
The user enters simultaneous editing mode by first describing the record set with positive and negative examples, using the same interaction techniques as selection guessing. Once the desired record set is obtained, the system enters simultaneous editing mode and the record set is highlighted in yellow (Figure 4). Now, when the user makes a selection in one record, the system automatically infers exactly one corresponding selection in every other record. If the inference is incorrect on some record, the user can correct it by holding down the Control key and making the correct selection, after which the system generates a new hypothesis consistent with the new example. As in selection guessing, the user can edit with the multiple selection at any time. The user is also free to make selections outside records, but no inferences are made from those selections.
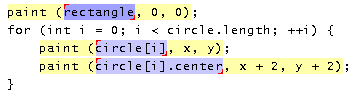
Simultaneous editing is more limited than selection guessing, because its hypotheses must have exactly one match in every record. But the one-selection-per-record constraint delivers some powerful benefits. First, it dramatically reduces the hypothesis search space, so that far fewer examples are needed to reach the desired selection. In the user study of simultaneous editing described later in this paper, the average selection needed only 1.26 examples, and 84% of selections needed only one. Second, the hypothesis search is much faster. Since the record set is specified in advance, LAPIS preprocesses it to find common substrings and library concepts that occur at least once, significantly reducing the space of features that can be used in hypotheses. As a result, where selection guessing might take several seconds to deliver a hypothesis, simultaneous editing takes 0.4-0.8 sec, making it far more suitable for interactive editing. Finally, the one-selection-per-record constraint makes editing semantically identical to single-selection editing on each record. In particular, a selection copied from one place in the record can always be pasted somewhere else, since the source and target are guaranteed to have the same number of selections.
In a long document, some of the inferred selections may lie outside the visible scroll area. LAPIS makes these selections easier to find by putting marks in the scrollbar corresponding to lines with selections (see, for example, the scrollbars in Figure 2). The user can scroll through the document to check that selections are correct before issuing an editing command. When there are many selections, however, checking them all can be tedious. LAPIS addresses this problem with outlier highlighting.
An outlier is an unusual selection, one that differs from the other selections in one or more features. For example, if all but one selection is followed by a comma, then the selection that doesn't have a comma could be considered an outlier. The more features in which a selection differs, the stronger the case for calling it an outlier. Briefly, our outlier finding algorithm computes the distance of each selection's feature vector from the median feature vector. If a small number of selections lie far from the median, then those selections are considered outliers.
Since outliers might be inference errors, LAPIS can highlight the outliers to draw the user's attention. The highlighting takes different forms depending on the inference mode. In selection guessing mode, outlier selections are colored red (instead of blue, the color used for ordinary selections). In simultaneous editing mode, however, the entire record containing the outlier changes color from yellow to red (Figure 5). Highlighting the record is more likely to catch the user's eye than highlighting just the selection, because a record occupies more screen area than a selection, particularly if the selection is just an insertion point. The red highlighting is also reflected as a red mark in the scrollbar, so that the user can find and check on outliers outside the visible scroll area.
Even when the document fits in the window without scrolling, however, outlier highlighting draws attention to inference errors. A user study of simultaneous editing [8] found that users noticed and corrected more inference errors with outlier highlighting (75%) than without (43%).

This section describes the algorithm used to infer multiple selections from positive and negative examples. The algorithm described here is used for selection guessing and the record definition step of simultaneous editing. Previous papers have described the other algorithms for simultaneous editing [7] and outlier finding [8].
Like most learning systems, the inference algorithm searches through a space of hypotheses for a hypothesis consistent with the examples. The hypothesis space is constructed from conjunctions of features, where a feature can either be a concept from the LAPIS structure library or a literal string found in the text. Whereas other PBD systems infer from a fixed set of low-level features, LAPIS can use any concept in its structure library to form features, including concepts that it would not otherwise be able to learn (e.g. Java syntax). Extending the feature set is as simple as adding a pattern to the library, which can be done by users.
Before describing the inference algorithm, we first briefly describe the representations used for selections in a text file. More detail can be found in an earlier paper about LAPIS [6]. A region [s,e] is a substring of a text file, described by its start offset s and end offset e relative to the start of the text file. A region set is a set of regions. Region sets are used throughout LAPIS: to represent multiple selections, structure library concepts, features, and hypotheses.
LAPIS has two novel representations for region sets. First, a fuzzy region is a four-tuple [s1,s2;e1,e2] that represents the set of all regions [s,e] such that s1 £ s £ s2 and e1 £ e £ e2 . Note that any region [s,e] can be represented as the fuzzy region [s,s;e,e] . Fuzzy regions are particularly useful for representing relations between regions. For example, the set of all regions that are inside [s,e] can be compactly represented by the fuzzy region [s,e;s,e] . Similar fuzzy region representations exist for other relations, including contains, before, after, just before, just after, starting (i.e. having coincident start points), and ending. These relations are fundamental operators in the LAPIS pattern language, and are also used to form features. These relations between intervals in a string are very similar to Allen's relations for intervals in time [1].
The second novel representation is the region tree, a union of fuzzy regions stored in a tree in lexicographic order [6]. A region tree can represent an arbitrary set of regions, even if the regions nest or overlap. A region tree containing N fuzzy regions takes O(N) space, O(NlogN) time to build, and O(logN) time to test a region for membership in the set.
A feature is a predicate defined over text regions. The inference algorithm uses two kinds of features: library features derived from the structure library, and literal features discovered by examining the text of the positive examples. Features are represented by a region set containing every region in the document that matches the predicate.
Library features are generated by prefixing one of seven relational operators to each concept in the structure library: equal to, just before, just after, starting with, ending with, in, or containing. For example, just before Number is true of a region if the region is immediately followed by a match to the Number pattern, and in Comment is true if the region is inside a Java comment. Thus, features can refer to context, even nonlocal context like Java or HTML syntax. Since the inference algorithm learns only conjunctions of features, LAPIS discards any library features that don't match every positive example.
Literal features are generated by combining the relational operators with literal strings derived from the positive examples. For example, starts with ``http://'' is a literal feature. We generate a starts with feature for every common prefix of the positive examples, but if two prefixes are equivalent, we discard the longer one. For example, starts with ``http'' is equivalent to starts with ``http://'' if ``http'' is always followed by ``://'' in the current document. Similar techniques generate literal features for ends with, just before, just after, and equal to. Literal features for contains are generated from substrings that occur in every positive example, which can be found efficiently with a suffix tree, a path-compressed trie into which all suffixes of a string have been inserted. More details about these feature generation algorithms can be found elsewhere [7].
After generating features that match the positive examples, LAPIS forms conjunctions of features to produce hypotheses consistent with all the examples. Since a selection must have a clearly defined start point and end point, not all conjunctions of features are useful hypotheses. We therefore reduce the search space by forming kernel hypotheses. A kernel hypothesis is either a single feature which fixes both the start and end (equal to F), or a conjunction of a start-point feature (starts-with F or just-after F) with an end-point feature (ends-with F or just-before F). All possible kernel hypotheses are generated from the feature set, and hypotheses inconsistent with the positive examples are discarded.
If there are negative examples, then additional features are added to each kernel hypothesis to exclude them. Features are chosen greedily to exclude as many negative examples as possible. For instance, after excluding negative examples, a kernel hypothesis equal to Link (which matches an HTML link element <a>...</a>) might become the final hypothesis equal to Link Ù contains "cmu.edu" Ù just-before Linebreak. Kernel hypotheses which cannot be specialized to exclude all the negative examples are discarded.
This simple algorithm is capable of learning only monotone conjunctions. This is not as great a limitation as it might seem, because many of the concepts in the LAPIS structure library incorporate disjunction (e.g. UppercaseLetters, Letters, and Alphanumeric). It is easy to imagine augmenting or replacing this simple learner with a DNF learner, such as the one used by Cima [5].
After generating a set of hypotheses consistent with all the examples, we are left with the problem of choosing the best hypothesis - in other words, defining the preference bias of our learner. Most learners use Occam's Razor, preferring the hypothesis with the smallest description. Since our hypotheses can refer to library concepts, however, many hypotheses seem equally simple. Which of these hypotheses should be preferred: Word, JavaIdentifier, or JavaExpression? We supplement Occam's Razor with a heuristic we call regularity.
The regularity heuristic was designed for inferring record sets for simultaneous editing. It is based on the observation that records often have regular features, features that occur a fixed number of times in each record. For instance, most postal addresses contain exactly one postal code and exactly three lines. Most HTML links have exactly one start tag, one end tag, and one URL.
It is easy to find features that occur a regular number of times in all the positive examples. Not all of these features may be regular in the entire record set, however, so we find a set of likely regular features by the following procedure. For each feature f that is regular in the positive examples (occuring exactly nf times in each positive example), count the number of times Nf that f occurs in the entire document. If f is a regular feature that occurs only in records, then there must be Nf/nf records in the entire document. We call Nf/nf the record count prediction made by f . Now let M be the record count predicted by the most features. If M is unique and integral, then the likely regular features are the features that predicted M . Otherwise, we give up on the regularity heuristic. The upshot of this procedure is that a feature is kept as a likely regular feature only if other features predict exactly the same number of records. Features which are nonregular, occuring fewer times or more times in some records, will usually predict a fractional number of records and be excluded from the set of likely regular features.
For example, suppose the user is trying to select the peoples' names and userids in the list below, and has given the first two items as examples (shown underlined):
Acar, Umut (umut)
Agrawal, Mukesh (mukesh)
Balan, Rajesh Krishna (rajesh)
Bauer, Andrej (andrej)
The two examples have several regular features in common, among them ``,'' (comma), which occurs exactly once in each example; CapitalizedWord, occurring twice; Word, three times; and Parentheses, once. Computing the record count prediction Nf/nf for these features gives 4 for comma, 4.5 for CapitalizedWord, 4.33 for Word, and 4 for Parentheses. The record count predicted by the most features is 4, so the likely regular features would be comma and Parentheses. This example is oversimplified, since the structure library would find other features as well.
|
|
| Multiple-selection | Equivalent task size | |||
| inference technique | Multiple-selection time | Single-selection time | novices | expert |
| Selection guessing | 426.0 [173-653] s | 43.0 [32-52] s/rec | 9.3 [4.7-15.7] recs | 2.3 recs |
| Simultaneous editing | 119.1 [64-209] s | 32.3 [19-40] s/rec | 3.6 [1.9-5.8] recs | 1.6 recs |
Likely regular features are used to test hypotheses by assigning a higher preference score to a hypothesis if it is in greater agreement with likely regular features. A useful measure of agreement between a hypothesis H and a feature F is the category utility P(H|F)P(F|H) , which was also used in Cima [5]. If a hypothesis and a feature are in perfect agreement, then the category utility is 1. We average category utility across all likely regular features to compute a score for the hypothesis.
Although the regularity heuristic was originally developed for inferring record sets in simultaneous editing, we have found that it works for selection guessing as well. The notion of regular features must be generalized beyond contains features, however, because selection guessing is often used to infer selections that don't contain any text at all, i.e. insertion points. Thus, the features just-before F and just-after F are considered regular features if positive examples contain no other occurrences of F , and in F is considered regular if every positive example is in a different instance of F .
Selection guessing and simultaneous editing were evaluated with two small user studies. Users were found by soliciting campus newsgroups - 5 users for the selection guessing study and 8 users for the simultaneous editing study. All were college undergraduates with substantial text-editing experience and varying levels of programming experience. All were paid for participating. Users learned about the inference technique they were going to use by reading a tutorial and trying its examples. The tutorial took less than 15 minutes for all users.
After completing the tutorial, each user was asked to perform one test task (Figure 6), obtained from Fujishima [3]. After performing the task with multiple selections, users repeated the first 3 records of the task with conventional, single-selection editing, in order to estimate the user's editing speed. Multiple-selection editing always came first, so time to learn and understand the task was always charged to multiple-selection editing. Single-selection editing always came second because we needed to measure the user's asymptotic, steady-state editing speed, without learning effects, in order to do the analysis described below.
The simultaneous editing study also had users do two other tasks which were omitted from the selection guessing study. More details about the full simultaneous editing study are found in a previous paper [7].
All 8 simultaneous-editing users were able to complete the task entirely with simultaneous editing, and 4 out of 5 selection-guessing users did, too. The fifth user also completed it, but only by exiting selection-guessing mode at one point, doing a troublesome part with single-selection editing, and then resuming selection-guessing to finish the task.
Aggregate times for the task are shown in Table 1. Following the analysis used by Fujishima [3], we estimate the leverage of multiple-selection editing by dividing the time to edit all records with multiple selections by the time to edit just one record with single selections. This ratio, which we call equivalent task size, represents the number of records for which multiple-selection editing time would be equal to single-selection editing time for a given user. Since single-selection time increases linearly with record number and multiple-selection time is roughly constant (or only slowly increasing), multiple-selection editing will be faster whenever the number of records is greater than the equivalent task size. (Note that the average equivalent task size is not necessarily equal to the ratio of the average editing times, since E[M/S] ¹ E[M]/E[S] .)
As Table 1 shows, the average equivalent task sizes are small. For instance, the average novice user works faster with simultaneous editing if there are more than 3.6 records in the test task. Thus simultaneous editing can win over single-selection editing even for very small repetitive editing tasks, and even for users with as little as 15 minutes of exposure to the idea. Selection guessing is not as fast as simultaneous editing on this task, primarily because selection guessing requires more examples for each selection. Both kinds of multiple-selection editing compare favorably with other PBD systems that have reported performance numbers. For example, when DEED [3] was evaluated with novice users on the same task, the reported equivalent task sizes averaged 42 and ranged from 6 to 200, which is worse on average and more variable than selection guessing or simultaneous editing.
Another important part of system performance is generalization accuracy. Each incorrect generalization forces the user to provide another positive or negative example. For all three tasks in the simultaneous editing user study [7], users made a total of 188 selections that were used for editing. Of these, 158 selections (84%) were correct after only one example. The remaining selections needed either 1 or 2 extra examples to generalize correctly. On average, 1.26 examples were needed per selection.
In the selection guessing study, users actually had two ways to correct an incorrect selection: either giving another example or selecting an alternative hypothesis. (The third method, correcting the hypothesis manually, was not available when the user study was done.) To judge the accuracy of selection guessing, we measure the number of actions a user took to create a selection, where an action is either giving an example or clicking on an alternative hypothesis. Of the 51 selections used in selection guessing, 34 (67%) were correct after only one action. On average, 2.73 actions were needed to create each selection used for editing.
After the study, users were asked to evaluate the system's ease-of-use, trustworthiness, and usefulness on a 5-point Likert scale, with 5 being best. The questions were also borrowed from Fujishima [3]. The average scores were quite positive for simultaneous editing (ease of use 4.5, trustworthiness 4.1, usefulness 4.3), but mixed for selection guessing (ease of use 3.6, trustworthiness 3.0, usefulness 4.8).
Inferring selections from examples may also be useful in applications that already use multiple selection, such as graphical editors, spreadsheets, and file managers. Even in the text domain, however, multiple-selection editing does not cover all cases where PBD is applicable. Multiple-selection editing is best suited to repetitive tasks where all the examples to be edited are present a single file - what might be called repetition over space. But PBD is also used for automating repetition over time, that is, creating a program that will be executed from time to time on new data. Good examples of repetition over time are email filtering rules and web page wrappers. Multiple selection editing might be applied to automating repetition over time by collecting some examples (e.g., from an email archive) and editing the examples with multiple selection. Inferred selections and the editing commands that use them would be recorded as a script that can be applied to future examples. If the script fails on some new example, the user would add the example to the example set and redemonstrate the broken part of the script on the entire example set, thereby guaranteeing that the script still works on old examples.
The low example count and fast response time of simultaneous editing make it a good candidate for future refinement. Supporting nested iterations (subrecords inside each record), conditionals (omitting some records from a multiple selection), and sequences (1-2-3, A-B-C, or Jan-Feb-Mar) would help simultaneous editing address more tasks. Since the user studies tested selection guessing and simultaneous editing separately, it is still an open question whether users can understand the difference between the two modes and determine when to use each one, or whether the two modes should be somehow combined into one. In retrospect, the name ``simultaneous editing'' is probably misleading, since all multiple-selection editing is ``simultaneous'' no matter how the selection is made.
Multiple selections offer a new way to automate repetitive text editing tasks. Two techniques for inferring multiple selections from examples were presented: selection guessing and simultaneous editing. Although selection guessing is the more general technique, simultaneous editing requires fewer examples and has faster response time.
LAPIS is a freely available, open-source program written in Java.
It implements all the techniques described in this paper: selection
guessing, simultaneous editing, and outlier highlighting. LAPIS can
be downloaded from:
http://www.cs.cmu.edu/rcm/lapis/
This research was supported in part by USENIX Student Research Grants.