
When users handle large amounts of data, errors are hard to notice. Outlier finding is a new way to reduce errors by directing the user's attention to inconsistent data which may indicate errors. We have implemented an outlier finder for text, which can detect both unusual matches and unusual mismatches to a text pattern. When integrated into the user interface of a PBD text editor and tested in a user study, outlier finding substantially reduced errors.
programming-by-demonstration, PBD, intelligent user interfaces, text editing, pattern matching, search-and-replace, LAPIS, cluster analysis, unsupervised learning
The search-and-replace command in a typical text editor forces users to choose between two alternatives: replace one match at a time with confirmation, or replace all matches at once. When the document is long and the number of matches large, neither choice is ideal. Confirming each match is tedious and error-prone. When most answers are Yes, a bored or hurried user eventually starts to press Yes without thinking. On the other hand, replacing all matches without confirmation requires the user to trust the precision of the search pattern. Reckless applications of global search-and-replace have been featured in comp.risks, among them ``eLabourated'' in a news report about the British government, ``back in the African-American'' in an article about a budget crisis, and ``arjpgicial turf'' on a web site that evidently switched from TIFF to JPEG [11].
We propose an alternative to these two extremes: outlier finding. In statistics, an outlier is a data point which appears to be inconsistent with the rest of the data [2]. Applied to search-and-replace, this idea means that the text editor highlights the most atypical pattern matches, so that the user can focus on the matches that are most likely to be problematic. Outlier finding reorganizes the search-and-replace task so that human attention - an increasingly scarce resource - is used far more efficiently.
Briefly, the outlier finder takes a set of text regions matching a target pattern, generates a list of binary-valued features describing the pattern matches and their context (such as ``starts with S'' or ``at end of a line''), tests the features against each match to compute a feature vector for the match, and finally sorts the matches based on their weighted Euclidean distance from the median match in feature vector space. Matches which lie far from the median are considered outliers. We have implemented an outlier finder as part of the LAPIS system (Lightweight Architecture for Processing Information Structure), a text-editor/web-browser designed for browsing and editing semi-structured text [7].
Outlier finding depends on two assumptions. First, most matches must be correct, so that errors are the needles in the haystack, not the hay. This assumption is essential because the outlier finder has no way of knowing what the user actually intends the pattern to match. Unless the set of matches is roughly correct to begin with, the outlier finder's suggestions are unlikely to be helpful. Second, erroneous matches must differ from correct matches in ways that are captured by the features. Although the outlier finder can be augmented with domain knowledge - ours has a substantial knowledge base, including a Java parser and HTML parser - the knowledge base inevitably has gaps, and the feature language may be incomplete. Fortunately, these assumptions are not seriously limiting. Outlier finding actually has more value when errors are like needles in a haystack, so the first assumption means only that it works better when it's more useful. As for the second assumption, we have found that many errors differ in dramatic ways from correct matches, often requiring no domain knowledge at all to detect.
Outlier finding is particularly useful for focusing human attention where human judgment is needed. The LAPIS system includes a novel user interface for automating repetitive editing tasks, called simultaneous editing [9]. Simultaneous editing uses multiple synchronized cursors to edit multiple locations in a document at once, inferring the locations of other cursors from the location of the cursor the user is controlling. Sometimes the other cursors are misplaced by a wrong inference, resulting in the wrong edits, but a user study found that users often overlook this error until it's too late [9]. In this paper, we show how outlier finding can be used to draw the user's attention to potentially-misplaced cursors, and present the results of a second user study in which outlier finding substantially reduced the frequency of this error.
Outlier finding can explore both sides of a set boundary - not only borderline matches to a pattern, but also borderline mismatches. Borderline mismatches can be even more valuable to the user than borderline matches, since the space of mismatches is usually much larger. In practice, finding near mismatches to a text pattern is complicated by the fact that the search space is the set of all substrings in a document. The problem can be simplified by reducing the search space - e.g., searching only words or lines, or ruling out mismatches that overlap a match.
Most work on outliers comes from the field of statistics [2], focusing on statistical tests to justify omitting outliers from experimental data. A large number of tests have been developed for various probability distributions. For the applications we are interested in, however, the distribution is rarely simple and usually unknown. Our outlier finder cannot make strong statistical claims like ``this outlier is 95% likely to be an error,'' but on the other hand it can be applied more widely, with no assumptions about the distribution of the data.
Outlier finding has been applied to data mining by Knorr and Ng [6], because outliers in large databases can yield insights into the data. Knorr and Ng propose a ``distance-based'' definition of an outlier, which is similar to our approach. They define a DB(p,D) outlier as a data object that lies at least a distance D (in feature space) from at least a fraction p of the rest of the data set. The choice of p and D is left to a human expert. Our algorithm is simpler for nonexpert users because it merely ranks outliers in a single dimension of weirdness. Users don't need to understand the details of the outlier finder to use it, and appropriate weights and parameters are determined automatically by the algorithm.
Our outlier finding algorithm draws on techniques better known in the machine learning community as clustering or unsupervised learning [1]. In clustering, objects are classified into similar groups by a similarity measure computed from features of the object. Clustering is commonly used in information retrieval to find similar documents, representing each document by a vector of terms and computing similarity between term vectors by Euclidean distance or cosine measures. Our application domain, text pattern matching, is concerned with matching small parts of documents rather than retrieving whole documents, so term vectors are less suitable as a representation. Freitag confirmed this hypothesis in his study of inductive learning for information extraction [4], which showed that a relational learner using features similar to ours was much more effective at learning rules to extract fields from text than a term-vector-based learner.
One way to find borderline mismatches in text pattern matching is to allow errors in the pattern match. This is the approach taken by agrep [15], which allows a bounded number of errors (insertions, deletions, or substitutions) when it matches a pattern. Agrep is particularly useful for searching documents which may contain spelling errors.
Spelling and grammar checking are well-known ways to find errors in text editing. Microsoft Word pioneered the idea of using these checkers in the background, highlighting possible errors with a jagged underline as the user types. Although spell-checking and outlier-finding both have the same goal - reducing errors - the approaches are drastically different. Spelling and grammar checkers compare the text with a known model, such as a dictionary or language grammar. Outlier finding has no model. Instead, it assumes that the text is mostly correct already, and searches for exceptions and irregularities. Whereas a conventional spell-checker would be flummoxed by text that diverges drastically from the model - such as Lewis Carroll's ``The Jabberwocky'' [3] - a spell checker based on outlier-finding might notice that one occurrence of ``Jabberwock'' has been mistyped because it is spelled differently from the rest. On the other hand, an outlier-finding spell checker would overlook systematic spelling errors. Morris and Cherry built an outlier-finding spell-checker [10] that computes trigram frequencies for a document and then sorts the document's words by their trigram probability, and found that it worked well on technical documents. We have not tried to apply our own outlier-finding algorithm to spell-checking, but it would make interesting future work.
Before delving into the details of the outlier-finding algorithm, we first describe how we used outlier finding to reduce errors in an intelligent text editor.
Simultaneous editing is a new user interface technique for automating repetitive tasks in text editing [9]. The user first selects a set of text regions to edit, called the records. For example, the records might be the entries in a bibliography, such as Figure 1. The user can select the record set in three ways: by making a multiple selection with the mouse, by writing a pattern in the LAPIS pattern language, or by giving one or more examples and letting LAPIS infer the rest.
After defining the records, the user makes a selection in one record using the mouse or keyboard. In response, the system makes an equivalent selection in all other records. Subsequent editing operations - such as typed text, deletions, or cut-and-paste - affect all records simultaneously, as if the user had applied the operations to each record individually. For example, the task in Figure 1 is to make each entry start with the author's name and year in square brackets. Figure 2 shows the desired result. To do part of this task, the user selects the author's name in one record and copies it to the beginning of the record. Simultaneously, the author's name in every other record is selected and copied.
A user study [9] found that novice users could do tasks like this one after only a 10-minute tutorial, and even small tasks (fewer than 10 records) were faster to do with simultaneous editing than with manual editing.


The greatest challenge in simultaneous editing is determining the equivalent selection where editing should occur in other records. Given a cursor position or selection in one record, the system must generalize it to a description which can be applied to all other records. Although our system's generalizations are usually correct (the user study found that 84% of users' selections were generalized correctly from only one example), sometimes the generalization is wrong. The user can correct a generalization by holding down the Control key and making a selection in another record - effectively giving another example of the desired selection - but the user must first notice that the generalization needs to be corrected.
In the user study, we observed that some incorrect generalizations are far more noticeable than others. Figure 3 shows an incorrect generalization that was easy for users to notice. The user has selected ``89'', the last two digits of the first record's publication year, which the system has mistakenly generalized into the description ``from just after first ``9'' to just after first year''. This generalization is drastically, visibly wrong, selecting far more than two digits in some records and nearly the entire last record. All eight users in the study noticed and corrected this misgeneralization.



The mistake in Figure 4, on the other hand, was much harder to spot. The user has selected the last name of the first author, ``Aha''. The system's generalization is ``first capitalized word'', which is correct for all but record 7, where it selects only the first half of the hyphenated name ``Hayes-Roth''. The error is so visually subtle that all seven users who made this selection or a related selection completely overlooked the error and used the incorrect selection anyway. (The eighth user luckily avoided the problem by including the comma in the selection, which was generalized correctly.) Although three users later noticed the mistake and managed to change ``[Hayes 95]'' to the desired ``[Hayes-Roth 95]'', the other four users never noticed the error at all. A similar effect was seen in another task, in which some users failed to notice that the two-word baseball team ``Red Sox'' was not selected correctly, resulting in errors.
In an effort to make incorrect selections such as Figure 4 more noticeable, we augmented the system with outlier finding. Whenever the system makes a generalization, it passes the resulting set of selected regions to the outlier finder. The outlier finder determines a set of relevant features and ranks the set of regions by the distance of each selection's feature vector from the median feature vector. The algorithm is described in more detail in a later section. Using this ranking, the system highlights the most unusual regions in a visually distinctive fashion, in order to attract the user's attention so that they can be checked for errors.
Two design questions immediately arise: how many outliers should be highlighted, and how should they be highlighted? Outliers are not guaranteed to be errors. Highlighting too many outliers when the selection is actually correct may lead the user to distrust the highlighting hint. On the other hand, an error may be an outlier but not the farthest outlier, so highlighting more outliers means more actual errors may be highlighted. But highlighting a large number of outliers is unhelpful to the user, since the user must examine each one. Ideally, the outlier finder should highlight only a handful of selections when the selection is likely to have errors, and none at all if the selection is likely to be correct.
After some experimentation, we found that the following heuristic works well. Let d be the weighted Euclidean distance of the farthest selection from the median and let S be the set of selections that are farther than d/2 from the median. If S is small - containing fewer than 10 selections or fewer than half of all the selections, whichever is smaller - then highlight every member of S as a outlier. Otherwise, do not highlight any selections as outliers. This algorithm puts a fixed upper bound on the number of outlier highlights, but avoids displaying useless highlights when the selections are not significantly different from one another.
The second design decision is how outlier highlighting should be rendered in the display. One possibility is the way Microsoft Word indicates spelling and grammar errors, a jagged, brightly colored underline. Experienced Word users are accustomed to this convention and already understand that it's merely a hint. In simultaneous editing, however, outlier highlighting must stand out through selected text, which is rendered using a blue background. A jagged underline would be too subtle to be noticed in this context, particularly in peripheral vision.
Instead, we highlight an outlier selection by changing its background from blue to red. To further enhance the highlighting, the entire record containing the outlier is also given a red background, and the scrollbar is augmented with red marks corresponding to the highlighted outliers. Simultaneous editing already augments the scrollbar with marks corresponding to the selection, so the red outlier marks are simply painted on top of the blue selection marks. Figure 5 shows the resulting display, highlighting two outliers in the erroneous author selection.
To evaluate the effectiveness of outlier highlighting, we repeated our original user study with new subjects. The only difference between the original study and the new study was the presence of outlier highlighting. The setup of both studies is briefly described below, and then the results relevant to outlier highlighting are discussed.
Users were found by soliciting campus newsgroups - 8 users for the original study with no outlier highlighting, and 6 users for the new study which included outlier highlighting. All were college undergraduates with substantial text-editing experience and varying levels of programming experience (in each group, roughly half described their programming experience as ``little'' or ``none,'' and half as ``some'' or ``lots''). All were paid for participating. Users first learned about simultaneous editing by reading a tutorial and trying the examples. This tutorial took less than 10 minutes for all but two users, who spent extra time exploring the system and making comments. The two groups received slightly different tutorials. Both tutorials discussed the problem of incorrect generalizations and gave users an exercise in correcting a generalization, but the outlier-highlighting group's tutorial also discussed what outlier highlighting looks like and what it means.
After completing the tutorial, each user performed the following three tasks using simultaneous editing:
Comparing the two groups of users, one with outlier highlighting and the other without, showed a reduction in uncorrected misgeneralizations, although the sample size was too small for statistical significance. The system's incorrect generalizations in these tasks fall into four categories:
Only tasks 1 and 3 have misgeneralizations. All selections in task 2 are generalized correctly from one example.
All users in both groups noticed that the Year selection was misgeneralized and corrected it, probably because the misgeneralization is dramatically wrong (Figure ). For the other two kinds of selections, the outlier highlighting algorithm correctly highlighted the errors in the selection. As a result, users seeing the outlier highlighting corrected the Author, Winner, and Loser misgeneralizations more often than users without outlier highlighting (Table 1). In particular, the Author misgeneralization, which was never noticed or corrected without outlier highlighting, was noticed and corrected 5 out of 8 times (63%) with the help of outlier highlighting. Users confirmed the value of outlier finding by their comments during the study. One user was surprised that outlier highlighting was not only helpful but also conservative, highlighting only a few places.
Because outlier highlighting encouraged users to correct misgeneralizations, it also reduced the overall error rate on tasks 1 and 3, measured as the number of tasks finished with errors in the final result (Table 2). Editing with a misgeneralized selection does not always lead to errors in the final output, because some users noticed the errors later and fixed them by hand. The error rate on task 2 increased, however, despite the fact that task 2 had no misgeneralizations to be corrected. One of these task 2 errors occurred because the user provided multiple inconsistent examples of one selection, a problem that was unfortunately exacerbated by outlier highlighting. This problem is discussed in more detail in the next section.
| Corrected misgeneralizations | ||||
| Year | Author | Winner | Loser | |
| Outliers | (task 1) | (task 1) | (task 3) | (task 3) |
| Not highlighted | 8/8 (100%) | 0/7 (0%) | 1/8 (13%) | 4/7 (57%) |
| Highlighted | 7/7 (100%) | 5/8 (63%) | 4/7 (57%) | 5/6 (83%) |
| Tasks completed with errors | |||
| Outliers | Task 1 | Task 2 | Task 3 |
| Not highlighted | 4/8 (50%) | 1/8 (13%) | 3/8 (38%) |
| Highlighted | 2/6 (33%) | 2/6 (33%) | 1/6 (17%) |
Although outlier highlighting reduced the number of errors users made, it did not eliminate them entirely. One reason is that the system usually took 400-800 milliseconds to compute its generalization, with or without outlier highlighting, and users did not always wait to see the generalization before issuing an editing command. For example, in the outlier-highlighting condition, 2 of the 3 uncorrected Author generalizations went uncorrected because the user issued an editing command before the generalization and outlier highlighting even appeared. After the user study, we changed the design so that records containing outliers remain highlighted in red through subsequent editing operations, until the user makes a new selection. As a result, even if the user doesn't notice an incorrect selection before editing with it, the persistent outlier highlighting hopefully draws attention to the error eventually.
Outlier highlighting also draws attention to correct generalizations, undeservedly. Several users felt the need to deal with the outliers even when the selection was correct, to ``get rid of the red'' as one user put it. Our design inadvertently encouraged this behavior by erasing the red highlight if the user provided the outlier as an additional example. As a result, several users habitually gave superfluous examples to erase all the outlier highlighting. Of the 143 total selections made by users with outlier highlighting, 16 were overspecified in this way, whereas no selections were overspecified by the users without outlier highlighting. To put it another way, the tasks in the user study required an average of 1.25 examples per selection for perfect generalization. Without outlier highlighting, users gave only 1.13 examples per selection, underspecifying some selections and making errors as a result. With outlier highlighting, users gave 1.40 examples per selection, overspecifying some selections. Giving unnecessary examples is not only slower but also error-prone, because the extra examples may actually be inconsistent. This happened to one user in task 2 - a correct generalization became incorrect after the user misselected an outlier while trying to erase its highlight, and the user never noticed.
After the study, we made several design changes to mitigate the problem of overspecified selections. First, selecting an outlier as an additional example no longer erases its outlier highlighting. Instead, users who want to ``get rid of the red'' must right-click on an outlier to dismiss its highlight, eliminating the danger of misselection. (This design was inspired by Microsoft Word, which uses the context menu in a similar fashion to ignore or correct spelling and grammar errors.) Second, the outlier highlighting was changed to make the outliers themselves blue, just like non-outliers, in order to make it clearer that a selection can be used for editing even if it contains outliers. Now, only the record containing the outlier is colored red. In simultaneous editing, each record contains exactly one selection, so there can be no ambiguity about which selection is the outlier.
In simultaneous editing, outlier finding is used behind the scenes to direct the user's attention to possible errors. Some users may want to access the outlier finder directly, in order to explore the outliers and obtain explanations of each outlier's unusual features. For example, suppose a user is writing a pattern to search and replace a variable name in a large program, and the user wants to debug the pattern before using it. For this kind of task, the LAPIS text editor provides the Unusual Matches window (Figure 6).
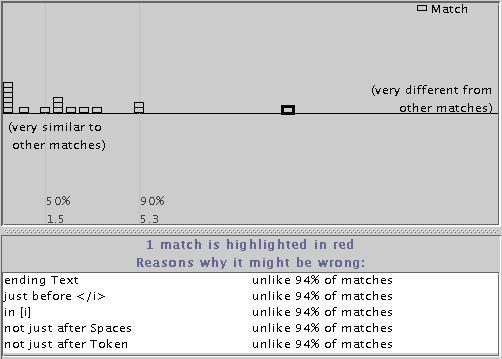
The Unusual Matches window works in tandem with the LAPIS pattern matcher. Normally, when the user enters a pattern, LAPIS highlights all the pattern matches in the text editor. When the Unusual Matches window is showing, however, LAPIS also runs the outlier finder on the set of matches.
Unlike the outlier highlighting technique described in the previous section, the Unusual Matches window does not use a threshold to discriminate outliers from typical matches. Instead, it simply displays all the matches, in order of increasing weirdness (distance from the median), and lets the user decide which matches look like outliers. Each match is plotted as a small block. Blocks near the left side of the window represent typical matches, being very close to the median, and blocks near the right side represent outliers, far from the median. The distance between two adjacent blocks is proportional to their difference in weirdness. Strong outliers appear noticeably alone in this visualization (Figure 6).
Matches with identical feature vectors are combined into a cluster, shown as a vertical stack of blocks. Matches that lie at the same distance from the median in feature space, but along different vectors, are not combined into a stack. Instead, they are simply rendered side-by-side with 0 pixels between them.
The user can explore the matches by clicking on a block or stack of blocks, which highlights the corresponding regions in the text editor (using red highlights to distinguish them from the other pattern matches already highlighted in blue). The editor window scrolls automatically to display the highlighted region. If a stack of blocks was clicked, then the window scrolls to the first region in the stack and displays red marks in the scrollbar for the others. To go the other way, the user can right-click on a region in the editing window and choose ``Locate in Unusual Matches Window'', which selects the corresponding block in the Unusual Matches window.
When a match is selected in the Unusual Matches window, the system also displays an explanation of how it is unusual (bottom pane in Figure 6). The explanation consists of the highest-weighted features (at most 5) in which the region differs from the median feature vector. If two features are related by generalization, such as starts with Letter and starts with UpperCaseLetter, only the higher-weighted feature is included in the explanation. Next to each feature in the explanation, the system displays the fraction of matches that agree with the median value - a statistic which is related to the feature's weight, but easier for the user to understand. The explanation generator is still rudimentary, and its explanations sometimes include obscure or apparently-redundant features. Generating good explanations is a hard problem for future work.
The Unusual Matches window can also show mismatches in the same display (Figure 7). When mismatches are displayed, the user can search for both kinds of bugs in a pattern: false negatives (mismatches which should be matches) as well as false positives (matches which should not be).
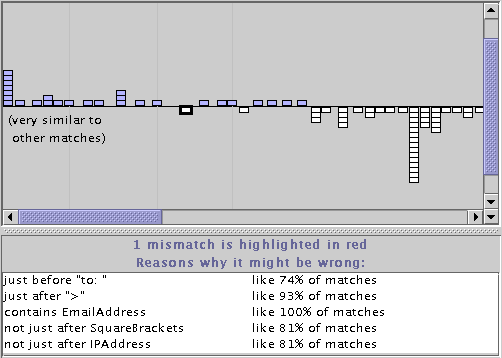
The tricky part of displaying mismatches is determining the set of candidate mismatches. The search space for pattern matching is the set of all substrings of the document. A naive approach would let the set of mismatches be the complement of the matches relative to the entire search space. Since this set is quadratic in the length of the document, we have come up with three reasonable ways to reduce the search space. Currently, LAPIS only implements the first:
Regardless of how the possible mismatches are defined, the Unusual Matches window plots each mismatch on the same graph as the matches. Mismatches are colored white and plotted below the horizontal midline to clearly separate them from matches. Like matches, mismatches with identical feature vectors are clustered together into a stack. Clicking on a mismatch highlights it in the text editor and displays an explanation of why it should be considered as a possible match. The explanation consists of the highest-weighted features in which the mismatch agrees with the median match. Figure 7 shows the explanation for a mismatch.
The Unusual Matches display offers users a new way to explore the set of pattern matches in a document. Instead of stepping through matches in conventional top-to-bottom document order, the user can jump around the Unusual Matches window. Clicking on outliers can help find exceptions and mistakes in the pattern, while clicking on typical matches can give confidence that the pattern is matching mostly the right things. If the Unusual Matches window were tightly integrated with a search-and-replace function - a step we have not yet taken in LAPIS - then the user might invoke Replace All on entire stacks of typical matches, but give the outliers more consideration before replacing them.
We now turn to the details of the outlier finding algorithm itself. The algorithm takes as input a set of data objects R (in this case, substrings of a document) and returns a ranking of R by each object's degree of similarity to the other members of R . Similarity is computed by representing each object in R by a binary-valued feature vector and computing the weighted Euclidean distance of each vector from the median vector of R . The distance calculation is weighted so that features which are more correlated with membership in R receive more weight. Features and feature weights are generated automatically from R , optionally assisted by a knowledge base (in this case, a library of useful text patterns).
If we want to find borderline mismatches, we use a related algorithm that takes two disjoint sets, R and [`R] , where R is the set of matches and [`R] is the set of mismatches. The algorithm then ranks the elements of both sets according to their similarity to R . Since this algorithm is used to find both matches and mismatches, we refer to it as the two-sided outlier finder. The simultaneous editing study only used one-sided outlier finding. The Unusual Matches window uses the two-sided outlier finder, but only when the user's pattern can be negated using the ``negated predicate'' technique described previously. Otherwise, the Unusual Matches window falls back to one-sided outlier finding. The discussion below focuses on one-sided outlier finding, mentioning the two-sided algorithm only where it differs.
The only part of these algorithms that is specific to text substrings is feature generation. Applying the algorithm to other domains would entail using a different set of features, but otherwise the algorithm would remain the same.
Before describing the outlier finder, we first briefly describe the representations used for selections in a text file. More detail can be found in an earlier paper about LAPIS [7].
A region [s,e] is a substring of a text file, described by its start offset s and end offset e relative to the start of the text file. A region set is a set of regions.
LAPIS has two novel representations for region sets. First, a fuzzy region is a four-tuple [s1,s2;e1,e2] that represents the set of all regions [s,e] such that s1 £ s £ s2 and e1 £ e £ e2 . Fuzzy regions are particularly useful for representing relations between regions. For example, the set of all regions that are inside [s,e] can be compactly represented by the fuzzy region [s,e;s,e] . Similar fuzzy region representations exist for other relations, including contains, before, after, just before, just after, starting (i.e. having coincident start points), and ending. These relations are fundamental operators in the LAPIS pattern language, and are also used in generalization.
The second representation is the region tree, a union of fuzzy regions stored in an R-tree in lexicographic order [7]. A region tree can represent an arbitrary set of regions, even if the regions nest or overlap each other. A region tree containing N fuzzy regions takes O(N) space, O(NlogN) time to build, and O(logN) time to test a region for membership in the set.
A feature is a predicate f defined over text regions. The LAPIS outlier finder generates two kinds of features: library features derived from a pattern library, and literal features discovered by examining the text of the substrings in R .
LAPIS has a considerable library of built-in parsers and patterns, including Java, HTML, character classes (e.g. digits, punctuation, letters), English structure (words, sentences, paragraphs), and various codes (e.g., URLs, email addresses, hostnames, IP addresses, phone numbers). The user can readily add new patterns and parsers to the library. Features are generated from library patterns by prefixing one of seven relational operators: equal to, just before, just after, starting with, ending with, in, or containing. For example, just before Number is true of a region if the region is immediately followed by a match to the Number pattern, and in Comment is true if the region is inside a Java comment. In this way, features can refer to the context around substrings, even nonlocal context like Java or HTML syntax.
Literal features are generated by combining relational operators with literal strings derived from the substrings in R . For example, starts with ``http://'' is a literal feature. To illustrate how we find literal features, consider the starts with operator. The feature starts with ``x'' is useful for describing degree of membership in R if and only if a significant fraction of substrings in R start with the prefix x . To find x , we first find all prefixes that are shared by at least two members of R , which is done by sorting the substrings in R and taking the longest common prefix of each adjacent pair in the sorted order. We then test each longest common prefix to see if it matches at least half the strings in R , a trivial test because R is already in sorted order. For all prefixes x that pass the test, we generate the feature starts with ``x''.
With a few tweaks, the same algorithm can generate literal features for ends with, just before, just after, and equal to. For example, the ends with version searches for suffixes instead of prefixes, and the just before version searches for prefixes of the text after each substring instead of in the substring itself. Only in and contains features cannot be generated in this way. The LAPIS outlier finder does not presently generate literal features using in or contains.
The two-sided outlier finder generates literal features by sorting both R and [`R] together, so that it considers literal features shared by any pair of matches or mismatches. However, a literal feature must be shared by at least half of R or at least half of [`R] to be retained as a feature.
After generating a list of features, the next step is determining how much weight to give each feature. Without weights, only the number of unusual features would matter in determining similarity. For example, without weights, two members of R that differ from the median in only one feature would be ranked the same by the outlier finder, even if one region was the sole dissenter in its feature and the other shared its value with 49% of the other members of R . We want to prefer features that are strongly skewed, such that most (but not all) members of R have the same value for the feature.
The one-sided outlier finder weights each feature by its inverse variance. Let P(f|R) be the fraction of R for which feature f is true. Then the variance of f is sf = P(f|R)(1-P(f|R)) . The weight for feature f is wf = 1/sf if sf ¹ 0 , or zero otherwise. With inverse variance weighting, features that have the same value for every member of R ( sf = 0 ) receive zero weight, and hence play no role in the outlier ranking. Features that are evenly split receive low weight, and features that differ on only one member of R receive the highest weight ( |R|/(|R|-1) ).
Two-sided outlier finding uses not only R but also [`R] to estimate the relevance of a feature. We want to give a feature high weight if it has the same value on most members of R , but the opposite value on most of [`R] . We use mutual information to estimate the weights [13]. The mutual information between a feature f and the partition R,[`R] is given by
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
After computing weights for the features, we prune out redundant features. Two features are redundant if the features match the same subset of R (and [`R] ) and one feature logically implies the other. For example, in a list of Yahoo URLs, the features starts with URL and starts with ``http://www.yahoo.com'' would be redundant. Keeping redundant features gives them too much weight, so we keep only the more specific feature and drop the other one.
We test for redundancy by sorting the features by weight and comparing features that have identical weight. Features are represented internally as region trees containing all the regions in the document that match the feature, and the system can quickly compare the two region trees to test whether the matches to one feature are a subset of the matches to the other. Thus the system can find logical implications between features without heuristics or preprogrammed knowledge. It doesn't need to be told that LowercaseLetters implies Letters, or that starts with ``http'' implies starts with URL. The system discovers these relationships at runtime by observing their effects.
Pruning does not eliminate all the dependencies between features. For example, in a web page, contains URL and contains Link (where Link is a library pattern that matches A elements) are usually strongly correlated, but neither feature logically implies the other, so neither would be pruned. The effect of correlated features could be reduced by using the covariances between features as part of the weighting scheme, but it is hard to estimate the covariances accurately without a large amount of data (accurately estimating the n2 covariances among n features would require O(n2) samples). Another solution would be to carefully design the feature set so that all features are independent. This might work for some domains, at the cost of making the system much harder to extend. One of the benefits of our approach is that new knowledge can be added simply by writing a pattern and putting it in the library. Thus a user can personalize the outlier finder with knowledge like CampusBuildings or ProductCodes or MyColleagues without worrying about how the new rules might interact with existing features.
The last step in outlier finding is determining a typical feature vector for R and computing the distance of every element of R from this typical vector.
For the typical feature vector, we use the median value of each feature, computed over all elements of R . Another possibility is the mean vector, but the mean of every nontrivial feature is a value between 0 and 1 , so every member of R differs from the mean vector on most features and looks a bit like an outlier as a result. The median vector has the desirable property that when a majority of elements in R share the same feature vector, that vector is the median.
After computing the median feature vector mf , we compute the weighted Euclidean distance d(r) between every r Î R and m :
|
The two-sided outlier finder also computes d(r) for members of [`R] . Members of [`R] with small d(r) values share many features in common with R , and hence are outliers for [`R] .
In practice, the running time of the outlier finding algorithm is dominated by two steps in the algorithm: (1) generating library features, which takes O(n|L|) time where L is the set of library patterns and parsers and n is the length of the document; and (2) testing library features against the regions in R , which takes O(|L|·|R|) time. The remaining steps - weighting, pruning, and ranking - are negligible. Fortunately, the set of library features is independent of R , so step (1) can be performed in the background before the outlier finder is used and cached for all subsequent calls on the same document.
Although we have only applied outlier finding to text pattern matching, it isn't hard to imagine applications in other domains. Outlier finding is well-suited to debugging a tricky selection or pattern. Examples in other domains include email filtering rules, database queries, selecting files to pack into a ZIP archive or back up to tape, or selecting the outline of a complicated object in a bitmap editor. Outlier finding could also be used to search for irregularities in application data, such as weird values in a spreadsheet or database. Most domains are actually easier for outlier finding than text because the search space consists of discrete objects, so the set of mismatches is obvious.
Some domains would require extensions to the outlier finding algorithm. Our outlier finder only uses binary-valued features, but other domains would require integer-valued or real-valued features (e.g. file sizes, spreadsheet values, pixel values). Text pattern matching could also benefit from integer-valued features (e.g., the number of occurrences of a library pattern or a literal string). Our outlier finder also considers only two classes of data objects, matches and mismatches, but more than two classes would be useful for some applications. Techniques for these kinds of extensions are plentiful in the machine learning literature [1].
Outlier finding has many applications to programming-by-demonstration (PBD) systems, such as simultaneous editing. PBD systems usually rely on the user to notice when the system has guessed wrong. With an outlier finder, however, a PBD system might be able to stop and ask the user about a weird example, instead of plowing blindly ahead and handling it incorrectly. Outlier finding might also detect when the user has provided inconsistent examples, another problem that plagues PBD systems, but only if the user provides enough examples to find meaningful outliers. Simultaneous editing required very few examples in our user study - only 1.25 examples per concept on average - so we were unable to test this idea.
This paper presented an algorithm for finding outliers in a text pattern match, demonstrated its application in the user interface of an advanced text editor, and presented user studies that show that outlier finding reduced errors.
The outlier-finding idea can be applied to any set of data objects, regardless of how it was created. The set may be the result of a description written by a user (e.g. a pattern match), a description inferred by a learning algorithm (e.g. a generalization in simultaneous editing), or even a selection made by the user (e.g., a group of selected files in a file browser). Given a useful set of features, the outlier finder can draw attention to unusual members in any set.
One usability danger of outlier finding is that users may grow to rely on the outlier finder to find all errors, which in general is impossible. The same problem exists with spell checkers, which have taken the place of proof-reading for many users, even though friend and fiend are equally acceptable to a spell-checker. One approach to this problem is to run other error checkers that fill in the gaps, much as a grammar checker can find some of the misspellings that a spell-checker overlooks.
Outlier finding can serve as a useful subroutine in an intelligent system, such as simultaneous editing and PBD, to help the system notice unusual data and bring it to the user's attention. Outlier finding enables a human user and a software agent to form a partnership in which each plays a role suited to their strengths: brute force computation to find possible mistakes, and fine human judgement to deal with them.
The system described in this paper is freely available for downloading from:
http://www.cs.cmu.edu/rcm/lapis/
This research was supported in part by USENIX Student Research Grants.