View synthesis for a virtual camera at arbitrary position and orientation, given many input views that are widely-distributed around an environment, is a very difficult problem. Two reasons that make this challenging are: (1) A method must be able to integrate information from images containing significant differences in the parts of the scene that are visible, and (2) since the desired results are photorealistic new views, a method must be "dense" so as to render images containing accurate texture and color information at every pixel.
We are developing a new approach called Voxel Coloring that reconstructs the "color" (radiance) at surface points in an unknown scene. Initially, we assume a static scene containing Lambertian surfaces under fixed illumination so the radiance from a scene point can be described simply by a scalar value, which we call color.
Coping with large visibility changes between images means solving the correspondence problem between images that are very different in appearance--a very difficult problem. Rather than use traditional methods such as stereo, we use a scene-based approach. That is, we represent the environment as a discretized set of voxels, and use an algorithm that traverses these voxels and colors those that are part of a surface in the scene. The advantage of this approach is that simple voxel projection determines candidates corresponding image pixels. A difficulty is that a given image pixel may not correspond to a particular projecting voxel if there is a closer voxel occluding the projecting voxel. For example, in the figure below the red voxel in the scene projects into the first and third images but not the second, because the blue voxel occludes it.

To solve this visibility problem we introduce a novel geometric constraint on the input camera positions that enables a single visibility ordering of the voxels to hold for every input viewpoint. This ordinal visibility constraint is satisfied whenever no scene point is contained within the convex hull of the input camera centers. Below are shown two simple camera configurations that satisfy this constraint. The left configuration shows a downward-facing camera that is moved 360 degrees around an object. The right configuration shows a rig of outward-facing cameras that are distributed around a sphere.
 |
 |
As a result of this camera constraint we can traverse voxels in increasing distance from the set of cameras. That is, we can first visit all voxels in the "layer" immediately adjacent to the convex hull of the cameras, then visit all voxels in the next layer immediately adjacent to the first layer, and so on. In this way, when a voxel is visited all other voxels that could possibly occlude the current one have already been visited and colored. Hence it is easy to check for each image whether or not the current voxel projects into (i.e., is visible in) the image. The following figure illustrates the voxel layers for one simple camera configuration.

Scene reconstruction is complicated by the fact that a set of images can be consistent with more than one rigid scene. Determining a scene's spatial occupancy is therefore an ill-posed problem because a voxel contained in one consistent scene may not be contained in another. On the other hand, a voxel may be part of two different consistent scenes, but have different colors in each. To cope with this problem we say a voxel V is color invariant with respect to a set of images if, for every pair of voxelizations S and T that contain V and that are consistent with the images, we have color(V, S) = color(V, T). Using this invariant, we define a voxel coloring of a set of images to be the maximally consistent coloring.
We can now define the complete voxel coloring algorithm as:
S={} /* initial set of colored voxels is empty
for i = 1 to r do /* traverse each of r layers
foreach V in the ith layer of voxels do
project V into all images where V is visible
if sufficient correlation of the pixel colors
then add V to S
Below are two examples of the voxel coloring algorithm, one of a scene containing a toy dinosaur (6cm x 8cm x 10cm), and the other of a real rose. In each case 21 input images (640 x 486 resolution) were captured by rotating the object 360 degrees (i.e., in increments of about 17 degrees) in front of a color camera (Sony XC-999 with 1/2" CCD sensor and 12mm, F1.4 lens) positioned approximately 30cm horizontally from the object center and 25cm vertically above the base of the object. The left image in each row is one of the 21 input images. The right two columns show the views rendered from the voxel reconstructions created by the algorithm. The results shown used a scene space decomposition into approximately 7M voxels (166 x 200 x 233 for the dinosaur, and 200 x 186 x 200 for the rose, for a scene-space resolution of about 0.5mm per dimension of each voxel), of which 72,497 were colored to represent the dinosaur and 71,655 to represent the rose. The runtime to construct this representation was approximately 3 minutes on a 250 MHz MIPS R4400 processor (SGI Indigo2 workstation). In contrast, a low-resolution scene decomposition of about 15K voxels (20 x 25 x 29 for the dinosaur) took less than 1 second to compute the 980 colored voxels representing the dinosaur, and the 750 colored voxels representing the rose.
Click on any of the images to view a larger version of each.
- Toy Dinosaur
Using a VRML-capable browser, you can interactively view the dinosaur reconstruction results: 4.3M VRML model or 530K gzip'ed VRML model. Note: The VRML model is not the same as the one used to create the images shown above. The VRML model is about 1/3 the voxel resolution in each dimension (about 7K voxels in the scene decomposition) in order to reduce the download time required.Input View Output Views 


- Rose
Input View Output Views 
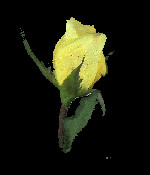

- Synthetic Room Scene
The last experiment consisted of a synthetic room scene containing three textured walls, a bust of Beethoven, and a human figure, illuminated diffusely from above. 24 images were synthesized corresponding to camera positions inside the room, with the optical axes of all the cameras parallel to the floor of the room. From these 24 input images the voxel coloring algorithm was applied to reconstruct this highly concave scene. The scene was decomposed by the algorithm into 2.3M voxels corresponding to a 150 x 125 x 125 resolution partitioning. The result of the algorithm was a coloring of 78,158 voxels representing the scene. The images below on the left are views synthesized directly from the room scene model (but do not correspond to any of the 24 input images), and the images on the right correspond to the same views, but synthesized from the voxel reconstruction produced by our algorithm.
Views Synthesized Directly from Model Corresponding Views Produced by Our Algorithm 


