the basic structure of the router follows the maze router algorithm outlined in lecture 13, with a few selected enhancements. basically, a wavefront of cells is expanded from the current source route until it encounters a target terminal. total pathcost and source direction are stored at each cell. when a terminal is found, the path is traced back to the nearest source cell.
peruse the pseudocode for exact algorithm details.
the data structures the router uses have been optimied for speed. memory usage was sacrificed in a few cases to reduce running time, however, total memory usage of the second largest benchmark was still under 20K.
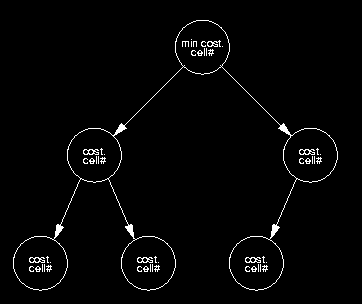
the most important data structure is probably the priority queue that represents the wavefront. profiling indicates that this structure is accessed a very large number of times even for small benchmarks. the priority queue implementation that was used is the "textbook" array based heap. this implementation saves some space from the pointer based version and allows for very fast lookup times. also, since the array only needs to be allocated once, time spent in the memory manager is reduced.
the heap is accessed with the standard operations:
insert()
| O(log n) |
remove_min()
| O(1) |
is_empty()
| O(1) |
heapify()
| O(log n) |
see the files
heap.c and
heap.h for implementation details.
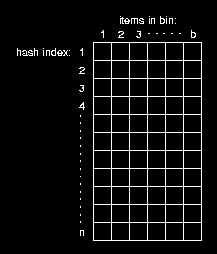
another interesting data structure is the hash table used to
find if the current cell is in the list of possible targets.
searching a linear array seemed to work quite well for all of the
smaller examples, but several designs in the big
directory have nets with well over 100 terminals. a hash table
data structure was created for searching for cells in the
termination list. hash table size and number of bins for each
hash value are fixed upon creation and are based on a simple
hueristic function of the basic netlist values. this hash table
is a good example of a data structure that was created in the
interest of speed and is somewhat insensitive to memory usage.
the actual hash table implementation is simply a one dimensional array that is treated as if it were two dimensional. this approach simplifies memory allocation and reduces overhead associated with memory allocation. Another benefit is that the insert/search/delete time of such an altorithm is O(b) the number of bins. which in this case is very small, giving an O(1) time for any hash table operation.
details of the hash table implementation can be found in
hash.c and
hash.h.
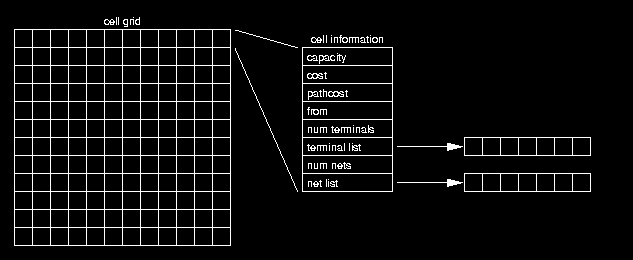
the grid cell data structure stores information about which nets and terminals are associated with each cell. it also keeps track of routing information while a net is being routed. The cells are stored as a one dimentional array of cell structures and all cell references are simply indices into the array.
see the file
route.h for details about the cell structure.