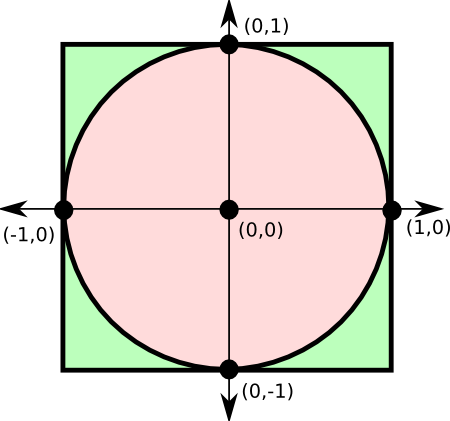
[3 points] Consider a unit circle (a circle of radius 1 whose center is at (0,0)) on a Cartesian plane, and a square whose corners are at (-1,1), (1,1), (1,-1), and (-1,-1). (Shown at right.). If a point is chosen randomly within the square, the probability of it being also within the circle is determined by the ratio of the area of the circle, \(\pi(1)^2 = \pi,\) to the area of the square, \(2^2 = 4.\) This concept can be implemented in Python to create a function that estimates \(\pi\).
Place the following functions in the file pi.py:
First, implement a helper function rnd_coord() that uses the Python randint function to generate and return a random floating point value between -1 and 1.
The function should be based on the following algorithm:
Generate a random integer between 0 and 2 billion, inclusive.
Subtract 1 billion from the result of the previous step.
Divide the result of the previous step by 1 billion (expressed as a floating point number) to obtain a random floating point value between -1.0 and 1.0.
Test your function a number of times to make sure it is operating correctly.
Example:
>>> rnd_coord() 0.671215514
Next, create a function est_pi(n) that returns an estimate of \(\pi\) computed using this procedure:
Repeat the following n times:
Randomly generate an x-coordinate and a y-coordinate for a point in the range -1.0 to 1.0 using your function above.
Determine whether the distance of the point from the origin ( \(\sqrt{x^2+y^2}\) ) is less than or equal to 1.0. These are the points "inside" the unit circle.
Compute the ratio of the total number of points inside the unit circle to the total number of points generated.
Multiply this ratio by 4 to obtain an estimate of \(\pi\) which should be returned from the function.
Note that the higher n is, the more accurate the estimate of \(\pi\) will be.
HINT: You will need a counter to keep track of the number of random points you generate that are "inside" the unit circle.
Examples:
>>> est_pi(5) 1.6 >>> est_pi(10) 3.6 >>> est_pi(100) 3.28 >>> est_pi(1000000) 3.140552
[4 points] The RandomLab in PythonLabs provides facilities for creating and manipulating Card objects.
Define the following functions in cards.py, which operate on Cards:
-
Define a function score21(hand), which takes an
array of RandomLab Card objects called hand and
computes and returns a score for that hand based on the
familiar card game Twenty One (Blackjack). Each card with
a numerical rank (2-10)
is scored worth that many points.
A card with a rank of jack, queen, or king should is worth
10 points. An Ace is worth 11 points, unless that would
put the total score over 21, in which case it is only worth
one point. The score for the hand is the sum of the points
for each of the cards.
Use the following algorithm:
-
Initialize score and num_aces to 0.
For each card in hand, do the following:
-
If the card is a 2, 3, 4, 5, 6, 7, 8, or 9,
add its numerical value to score.
(THINK: This shouldn't require 8 separate blocks of code!) If the card is a 10, J, Q or K, add 10 to score.
(THINK AGAIN: This shouldn't require 4 separate blocks of code!) If the card is A (Ace), add 11 to score and add 1 to num_aces.
-
If score is greater than 21,
subtract 10 from score.
Examples:
>>> h = [Card(50), Card(34), Card(12)] >>> h [K♠, 10♥, A♣] >>> score21(h) 21 >>> h = [Card(12), Card(32), Card(45)] >>> h [A♣, 8♥, 8♠] >>> score21(h) 17
Write a function majority_red(hand) that takes a hand of \(n\) cards and returns True if more than \(n/2\) cards in hand have a red suit (that is, are either hearts or diamonds).
Examples:
>>> h = [Card(12), Card(32), Card(45), Card(20)] >>> h [A♣, 8♥, 8♠, 9♦] >>> majority_red(h) False >>> h = [Card(12), Card(32), Card(45), Card(20), Card(34)] >>> h [A♣, 8♥, 8♠, 9♦, 10♥] >>> majority_red(h) True
[3 points] A simplified version of the dice game Hazard is played as follows: For each round, a integer from 5 through 9 (inclusive) is chosen; this is called the "main" for that round. Each round proceeds with a first phase. In the first phase, two dice are rolled and the values showing on the two dice are added together. If the sum is the "main" value, the player wins that round. If the sum is 2 or 3, the player loses that round. If the sum is neither the "main" value, 2, nor 3, that sum is called the "chance", and play proceeds by re-rolling the two dice repeatedly until their sum is either "main" or "chance". If the sum is "main", the player wins the round. If this sum is "chance", the player loses the round.
Download the file hazard.py, which includes a function roll_pair() that you should call to roll a pair of dice and get their sum. Add the following functions to hazard.py:
First, create a function phase_one(main), that, based on the result of a call to roll_pair, returns 1 for a "win", 0 for a "lose", or the value that should be used as the "chance" according to the rules described above. Before calling roll_pair, the function should print a header line with the value of main, so that the output matches the format of the following examples:
>> phase_one(7) Phase 1 with main=7 1st die: 1 2nd die: 3 sum: 4 4 >> phase_one(6) Phase 1 with main=6 1st die: 4 2nd die: 2 sum: 6 1 >> phase_one(5) Phase 1 with main=5 1st die: 1 2nd die: 1 sum: 2 0
You may assume that the function will only be called with a main of 5, 6, 7, 8, or 9.
Next, create a function phase_two(main, chance) that repeatedly calls roll_pair until the sum matches either main or chance. (Hint: Use a loop here!) If the sum matches main first, the function should return 1 for a "win". If the sum matches chance first, the function should return 0 for a "lose". In addition, the function should print a header line with the values of main and chance so that the output matches the format of the following examples:
>>> phase_two(7,4) Phase 2 with main=7 and chance=4 1st die: 2 2nd die: 6 sum: 8 1st die: 1 2nd die: 4 sum: 5 1st die: 6 2nd die: 4 sum: 10 1st die: 1 2nd die: 1 sum: 2 1st die: 1 2nd die: 4 sum: 5 1st die: 3 2nd die: 3 sum: 6 1st die: 1 2nd die: 2 sum: 3 1st die: 3 2nd die: 6 sum: 9 1st die: 2 2nd die: 1 sum: 3 1st die: 6 2nd die: 4 sum: 10 1st die: 3 2nd die: 3 sum: 6 1st die: 5 2nd die: 3 sum: 8 1st die: 4 2nd die: 2 sum: 6 1st die: 3 2nd die: 4 sum: 7 1 >>> phase_two(9,5) Phase 2 with main=9 and chance=5 1st die: 2 2nd die: 4 sum: 6 1st die: 4 2nd die: 4 sum: 8 1st die: 2 2nd die: 2 sum: 4 1st die: 3 2nd die: 1 sum: 4 1st die: 2 2nd die: 2 sum: 4 1st die: 4 2nd die: 3 sum: 7 1st die: 4 2nd die: 1 sum: 5 0
You may assume that phase_two will only be called with a main that is at least 5 and at most 9, and a chance of at least two and at most 12 and that main and chance are not equal.
Finally, create a function hazard(main) that simulates one round of Hazard, returning the strings "win" or "lose" as appropriate. It should follow the rules described above and produce output matching the pattern of the example shown below:
>> hazard(6) Hazard with main=6 Phase 1 with main=6 1st die: 6 2nd die: 1 sum: 7 Phase 2 with main=6 and chance=7 1st die: 4 2nd die: 1 sum: 5 1st die: 4 2nd die: 1 sum: 5 1st die: 3 2nd die: 2 sum: 5 1st die: 2 2nd die: 4 sum: 6 'win' >>> hazard(6) Hazard with main=6 Phase 1 with main=6 1st die: 3 2nd die: 3 sum: 6 'win' >>> hazard(6) Hazard with main=6 Phase 1 with main=6 1st die: 3 2nd die: 2 sum: 5 Phase 2 with main=6 and chance=5 1st die: 4 2nd die: 6 sum: 10 1st die: 3 2nd die: 2 sum: 5 'lose'
This function should be implemented by making calls to your helper functions phase_one and phase_two that you wrote earlier.
You may assume that the function will only be called with a main of 5, 6, 7, 8, or 9.